浅谈高职高专数学教学法

钟艳林

【摘要】高职高专数学难教是不争的事实。目前，高职高专学生普遍存在数学基础差、学生上课听不懂等问题。因此，如何使学生上课能听懂成为老师最关心的问题。笔者5年来一直从事高职高专的数学教学工作，体会颇深。现将这些体会作一系统的总结，希望能与各位同仁共同交流。

`【关键词】高职高专 数学教学法 知识点 表达语言 和谐师生关系

早在2000年，教育部的2号文件就指出：“高职高专教育的培养目标是培养拥护党的基本路线，适应生产建设、管理、服务第一线需要的德、智、体、美全面发展的高等技术适用性专门人才；学生应具有必备的理论和专业知识基础上，重点掌握从事本专业领域实际工作的基本能力和基本技能，具备良好的职业道德和敬业精神”。

这里十分明确地指出了高职高专院校的培养目标是高等技术应用性人才，不是学科型、研究型的人才，实际工作的基本能力和基本技能为重点，基础理论以“必需，够用”为准则。因此，教学计划，教学大纲必须以培养高等技术应用性人才为根本任务，以社会需要为目标，以培养技术能力为主线来设计。目前，各高职高专院校已基本完成了教学计划和各科教学大纲的制订，并已进行了几个学期的教学工作。

笔者经过几个学期的《经济数学》教学工作，深刻地体会到，教师在教学过程还要进一步地根据培养目标处理教学中的问题，而且教学方法比本科生、研究生教学更加重要。因为高职高专学生具备更多的特殊性，诸如，中学教学基础知识参差不齐，学过的知识很不牢固，学习方法和自学能力不强。下面谈几个确实对教学很有实际意义的问题。

一、对教学大纲每一最小知识点进一步细化

从培养目标出发，合理地确定基本要求，做到教学内容方面的少而精。就函数一节求函数定义域这个具体的小知识点来论，求函数定义域问题可细化为许多种。如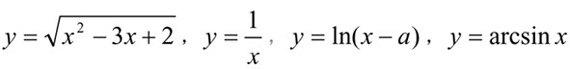，等，还有它们的交叉复合、四则运算，分段函数。解定义域又需许多相关知识，如解第二个函数定义域需要会解一元二次不等式，而反三角函数学生又十分陌生。要全部搞清这些问题，对高职高专学生而言，一、二个学时也未必掌握，所以教学必需根据培养目标，以“够用”为原则，舍其大部，合理确定基本要求，比如，只限定在上述第一、第四个函数及其四则运算情形。教师合理地明确基本要求，使教者明确，学生重点练习，就可以提高教学质量。否则，教师举例题与出练习题，摇摆不定，学生抓不住重点，弄成什么也学不会。

二、基本概念抓住本质而不过分追求形式，基本理论抓住条件与结论的分析，而不过分追求数学上的证明

基本概念是理论体系的基础，基本理论是课程体系的核心，而基本计算是课程应用的主体。基本概念不理解，就学不好数学。就极限概念来论，它是微积分的核心概念——导数与积分的基础，是用运动观点处理问题的数学方法，是一个基本概念。然而，其精确的定义，对学生有难度。学过高等数学的同志都知道，真正掌握极限的定义需要一定的时间，再考虑自变量的不同变化过程在内，共有七种形式，考虑函数趋于无穷大的情形，又各有三种，这对高职高专学生难上加难。但是采用描述性语言定义，即把极限作为描述自变量某一变化过程中，函数的变化趋向就容易得多，而且描述法定义更清楚地反映了极限的本质，对于以后的应用毫无影响，因此目前采取描述法定义极限概念。其实，传统数学体系中，为了理论体系易于展开，而选取定义形式的个案，也早已存在，如概率中连续型随机变量的定义，就是一个例子。

三、要善于创造性地提出各种不同的解题方法，然后不断地从学生易于接受的角度进行方法的优化

哪怕一些小问题，也要在比较中选择较好的方法。如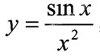，求y′时。可有两种方法如下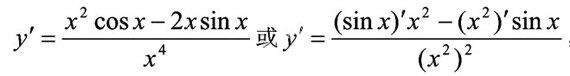：，然后再化简，初学者认为后一种更好，易于理解。教师和导数公式较熟练者认为前者简单不罗嗦，对高职高专学生使用后者较好!再如，记忆和叙述导数公式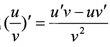时，有经验的老师教学生“分式的导数等于：分子的导数乘以分母，减去分子乘以分母的导数，然后除以分母的平方。”这种写的是的u，v的公式，说的是方块字的方法。实际证明相当方便。教师的无数经验教给学生，教学方法就活了。

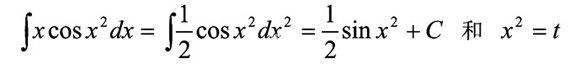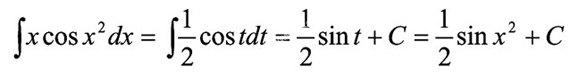在不定积分换元后两种方法，前者是凑微方法，后者是换元法，学生哪一种易于接受，也是需要在使用中看学生的接受情况来评价。

四、搭建起学生新旧知识的过渡平台

高职高专学生对许多学过的知识模模糊糊，在新形式下应用时常常困难，一次积分运算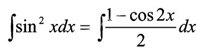中，尽管教师说明这一步运用三角函数半角公式，可是许多学生仍处于“麻木”状态，于是老师进一步指出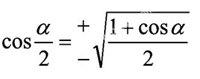和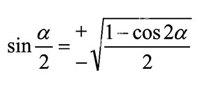，大部分同学才说有这回事，那么α=2x不就是这一步运算吗!如此温故知新，巩固了旧知识，理解了新知识，一举两得。如果不提出中学形式的半角公式，许多学生就解决不了新知识与旧知识的联系。这里的思想就是，不是学生服从于老师的讲法，而是老师服务于学生，从学生易于接受的角度去选择方法。

五、大力采用各种问式教学法

教学是师生双边活动，这是问式教学法常胜不衰之根本原因。老师自问自答、师问学生整体答、提问个别学生答、师问谁会谁答，问式教学法可以有多种形式。通过问，可以了解学生掌握知识情况，可以调动学生思考，可以突出重点，可以复习巩固公式，可以纠正学生错误，可以启发学生去解决问题，可以活跃课堂气氛……教师要养成在问中解决问题的习惯，善于相互讨论，共同解决问题。教师的一次教学课，可以在设计一系列的问题中不断提出问题，不断解决问题。如不定积分的第一次课，可以提出下面一些问题：函数f(x)的原函数概念，怎样的函数存在原函数，一个函数存在原函数时，原函数有多少个? F′(x)=f(x)时，F(x)+C是否是f(x)的全体原函数，f(x)的不定积分就是的全体原函数，怎样证明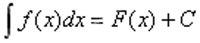?由基本导数公式怎样得出一系列的不定积分基本公式?怎样证明不定积分的线性性质……等等，在这一系列问题中展开教学，环环相扣，使教学在不断提出问题，不断解决问题中进行。

总之，笔者认为，教法无常规，常因教学目的不同，学生掌握知识的情况不同而变化，需要不断创新，与时俱进。在现今高职高专教育条件下，在现今这一阶段的高职高专学生的具体情况下，教学方法会渐趋成熟。愿高职高专数学教学更上一层楼。

参考文献：

[1]李玉保.论教学方法与教学手段的改革.2002，4.

[2]雷学忠.数学素质教育和建构主义教学.2002，2.