谈学生的课堂说话

祁　铮

【摘 要】当前的数学课堂，要求教师在上课时不但要注重传授知识和对学生进行各种能力的培养，而且要引导好师生之间、学生之间的信息传递，进行师生之间的情感交流，引发师生间思维的碰撞，真正体现学生是学习的主人，为学生的主动学习搭设平台，让学生去说，让学生去参与，让学生去思考。

【关键词】数学课堂 说话 主动参与

数学课堂上，教师不但要注重传授知识和对学生进行各种能力的培养，而且引导好师生之间、学生之间的信息传递，进行师生之间的情感交流，引发师生间思维的碰撞，真正体现学生是学习的主人，充分发挥其主动性。要创造各种机会，让学生去参与，让学生去思考，为学生的主动学习搭设平台，让学生去说，让学生去做。同时，要创造出一种宽松的环境，使学生敢想，使学生敢说，使学生敢做。在实际教学中，我就注意让学生多思考、多说，引导学生活泼、主动地学习。

一、让孩子先说话

在数学课上，我特别喜欢让孩子们先说话。让学生先说话，既可以是教师把握学生掌握知识的状况，避免超前，防止滞后，根据学生的认可程度来决定如何来“导”，增强教学的针对性；又可以给学生充分的参与机会。

例如，在学习“年、月、日”一课时，我先发给孩子们每人一张不同年份的小小年历卡，让学生先仔细地观察，然后说说“通过观察，你知道了什么？”学生们说的可多了：一年有12个月，1、3、5、7、8、10、12月都是31天，2、4、6、9、11月都是30天，2月是28天，有时是29天。哪些月的天数相同，哪些月的天数不相同，那个月是特殊的，特殊的这个月情况又是如何等等。许多老师要讲的内容学生都先说出来了，当然也就没有必要再由教师一条一条地、平铺直叙的讲给学生听了。

又如，在学习“圆的认识”一课时，我考虑到“圆”是一种平面图形，尽管学生没有学过由曲线围成的封闭图形，但是在实际生活中，他们见过无数平面是圆的实物。因此，我让学生先说话：“你在生活中见过哪些圆？”学生随之会列举出大量的圆，其中也会出现一种误解，即误认为地球也是圆。这个错误的出现是好事，它恰恰说明了学生认识上的误区，此时，正需要教师的“导”，而只有针对学生的问题去“导“才能体现教学的高效。我随即拿出一个事先准备好的球，与同学们列举的其它例子做比较，如桌子的面、盘子的口，等等。引导学生观察比较：“它一样吗？怎么不一样？”通过比较，学生发现，球不是圆的，而是立体的。由此，学生知道了“我们讲的圆一种平面图形，而球是一种“体”。球和圆是两种不同的概念，它们又有什么联系呢？老师将球一分为二，学生看到横截面。“横截面是圆！”孩子们兴奋地喊了出来。

由此可见，孩子们是可以先说话的，孩子们先说话是使知识学习与能力的训练同步进行，同步深入。让学生把自己发现的说出来，实际上就是观察和思考的结果。如果一些知识、一些规律由教师讲，也可以得到学生的共识，这样做却是剥夺了孩子们观察思考的权利，抢占了孩子们亲自参与的机会和发表意见的时间。

二、巧用“学生的话”

课堂上，学生常常会有些很有意思的话，如果教师能够及时地抓住这些“话”，巧用这些“话”，就会有意想不到的效果，常常会使课堂教学出现一些让人记忆深刻、甚至终身难忘的闪光点。

在讲“分数的意义”这一课时，在师生共同研究并概括出了“什么叫分数”，明确认识了单位“1”、分数单位以及分母、分子和各自的意义之后，我提出了这样一个问题：“如果让你写一个分数，你怎么写？是从上往下写？还是从下往上写呢？”一个平时不爱讲话的男孩被我叫了起来，他一站起来就极其肯定地说：“应该先写分数线，然后从下往上写。也就是要先写分母，再写分子。”我追问到：“为什么呢？”“因为……因为……”他犹豫着，声音越来越小。其他同学有些按捺不住，高高地举起手。我示意大家把手放下，然后，亲切地对这个男孩说：“你刚才说的又对又清楚，一定想得也很好，怎么想的呢？说给大家听听好吗？”听我这么说，他鼓起勇气说了一句：“没有妈哪来的儿子？”同学们愣住了，我也愣了一下，太出乎意料的回答！但我立刻明白了孩子的意思。“没有妈哪来的儿子？”我重复了一遍他的话，接着说：“这个比方打得好！告诉大家这是什么意思。”这下，他兴奋了，声音也大了，他说：“分母表示平均分的份数，分子表示所取的份数，先有平均分数的份才能有所取的份数，所以把平均分的份数叫分母，把取的份数叫分子，不就像先有妈后有儿子吗？”听他这么一解释，大家恍然大悟，忍不住开心地笑起来。我呢，也同大家一道开心地笑，边笑边用赞许的目光示意他坐下。然后，我说道：“这位同学说的挺好，他的思维很活跃，比喻也还恰当，后边的解释也挺到位，语言还挺幽默。”大家情不自禁又学说着：“没有妈哪来的儿子？”气氛一下子又活跃了起来。在这开心的笑声中，大家进一步了解了分母、分子的意义，记住了分数的写法；在这开心的笑声中，这个小男孩有了自信和成功的愉悦；在这开心的笑声中，师生的思维和情感都是相互碰撞的，碰撞出点点火花……

三、让孩子们总结

虽然，让孩子来总结有一定难度，但是这个阶段如果仍是教师“一言堂”，则不能说学生参与了教学活动的全过程，不利于培养学生主动学习的精神。是否由学生来总结，是学生总体作用发挥如何的一个很重要的标志。这是因为由学生来总结具有非同一般的积极意义。

如教学“平面几何的图形面积计算”总结时，先由学生按照学习的先后顺序，一一说出所学的长方形、正方形、平行四边形、三角形、梯形、圆的平面图形，然后，复习长方形面积计算方式，进而提出问题：“长方形面积计算与后边所学的图形面积计算之间的联系是什么？”同学们思考着、讨论着，最后梳理并且总结如下。

长宽相等的长方形是正方形，所以正方形面积是边长乘边长；平行四边形可以分割转化成长方形，所以平行四边形的面积是底×高；两个完全相等的三角形可以拼成一个平行四边形，所以三角形面积是底×高÷2；两个完全相等的梯形可以拼成一个平行四边形，梯形上下底之和等于平行四边形的底，所以梯形面积是（上底+下底）×高÷2；圆形也可以分割后拼摆转化成平行四边形，圆周长的一半相当于平行四边形的底，圆半径相当于高，所以圆面积等于圆周长的一半乘以半径即πr²。

还可以用这样的图表示他们之间的关系：

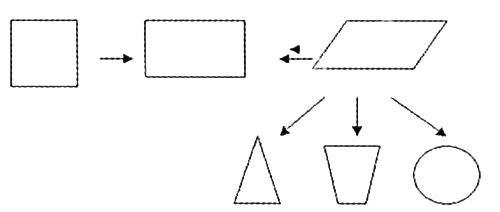
可见，通过自己的复习、总结，学生不仅梳理了知识，同时，梳理了思路与方法。同学们的头脑中不再是一个一个孤立的公式，而是一个相互与联系的知识网。在总结这些公式的推导过程中，学生必然在研究问题、学习知识的方法上有所收益。这进一步强化了怎么样利用旧知识研究一个新问题的思路和能力，也恰恰是我们课堂教学所追求的真正效果。