游戏开发案例在数据结构教学中的应用实践

管士亮

文章编号：1672-5913(2009)06-0132-04

摘要：“数据结构”课程是计算机专业最重要的专业基础课，游戏开发技术是计算机应用技术最前沿的分支之一，实现由基础到前沿的跨越，是学生的希望所在，也是检验教学成功与否的重要指标。本文总结了游戏开发过程中的成功经验，及时反馈并自觉落实到教学过程中，对教师和学生都是有益的尝试。

关键词：数据结构；游戏开发；跨越

中图分类号：G642

文献标识码：B

从事“数据结构”教学的教师往往遇到的学生困惑是：数据结构有什么用？数据结构与计算机新技术的开发有什么关系？类似的问题一方面反映了学生对计算机新技术的渴望与困惑；另一方面也反映了“象牙塔”里的学校教育与技术开发市场之间的距离。

毋庸置疑的是，“数据结构”是计算机本科学生最重要的专业基础课，在游戏编程中扮演着极其重要的角色，而游戏开发技术又是计算机应用技术最前沿的分支之一。本文试图通过数据结构在游戏开发中的简单应用来解答学生的困惑，以此拉近学校教育与市场开发之间的距离。本文涉及到数据结构中的链表、顺序表、栈、队列、二叉树及图的概念，在此不做过多描述，希望读者阅读本文前对数据结构有所了解，并且熟悉C/C++语言的各种功能和应用。

1顺序表的应用

顺序表是数据结构中最简单、最常用的一种线性表，它的特点是，用一组地址连续的存储单元依次存储线性表的元素。砖块地图系统中使用的就是这种最简单的数据结构。这里对砖块地图系统做如下规定：构建一个简单的砖块地图系统，视角为俯视90度，并由许多个顺序连接的图块拼成。

(1) 定义图块

struct Plot //定义图块结构

{

int Access; //记录此图块是否可以通过

…… //中有每个图块的图片指针 等记录

};

Access为0时，表示此图块不可通过，为1表示能通过。

(2) 定义二维数组存放每个图块的值

定义的二维数组为：Plot Map[7][10]。通过循环将此地图初始化，初始化程序和生成地图如图1所示。

for (i=0;i<=6;i++)

for (j=0;j<=9;j++)

scanf(“输入第%行，第%列初始化值:%d ”&i,&j,&Map [i][j]);

从图1看出，这个地图用顺序表表示非常直接。当控制人物在其中走动时，对人物将要走到的下一个图块进行判断，看其是否能通过。比如，当人物要走到(2，5)这个图块时，用如下判定函数来判断这个图块是否能通过：

x=3;y=5;

int Ispass(x,y)

{

return Map[x,y].Access; //返回图块是否 通过的值

}

以上只是简单的地图例子，使用顺序表也可以表示更为复杂的砖块地图。目前流行的整幅地图中也都要用到大量的顺序表，只不过在整幅中进行分块而已。

2链表应用

链表的主要优点就是可以方便地进行插入、删除操作。在游戏开发中，链表主要应用在有大规模的删除和添加操作上。在飞机游戏中，飞机的子弹是要频繁地出现、消除的，个数也是随机的。链表主要应用在发弹模块上。在下面的源代码中，我们就定义了坐标结构和子弹链表。

(1) 定义坐标结构

struct Cpiot //定义坐标结构

{

int x; //X轴坐标

int y; //Y轴坐标

};

(2) 定义子弹链表

struct Bullet //定义子弹链表

{

Cpiotbulletpos; //子弹的坐标

intbulletspd; // 子弹的速度

struct Bullet* next; //指向下 一个子弹

};

(3) 定义飞机类中的子弹

class Cmyplane

{

public:

void AddBullet(struct Bullet*);

//加入子弹的函数，每隔一定时间加弹

void RefreshBullet();

//刷新子弹

privated:

struct Bullet *St_MyBullet;

// 声明飞机的子弹链表

};

在void AddBullet(struct Bullet*)中，只要将一个结点插入链表中，并且每隔一段时间加入，就会产生连续发弹的效果。

(4) 加弹函数的主要源代码

void AddBullet(struct Bullet*)

{

struct Bullet *St_New,*St_Temp;

//定义临时链表

St_New=_StrucHead; //链表头(已初始化)

St_New->(Bullet St_MyBullet *)malloc (sizeof(St_MyBullet));

//分配内存

St_Temp= =_NewBullet; //临时存值

St_New->next=St_Temp->next;

St_Temp->next=St_New;

}；

(5) 在函数Void RefreshBullet()中，只要将链表遍历一次，就可以实现子弹的数据更新。主要的源代码如下：

while(St_MyBullet->next!=NULL)

{ // 查找

St_MyBullet->bulletpos.x=bulletspd;

//更新子弹数据

………

St_MyBullet=St_MyBullet->next;

//查找运算

};

3栈和队列的应用

栈和队列是两种特殊的线性结构，在游戏程序开发中，这两种线性结构一般应用在脚本引擎、操作界面、数据判定中。下面通过一个简单的脚本引擎函数来介绍栈的应用。队列和栈的用法很相似，可依此类推，不再举例。

设置脚本文件的时候，通常会规定一些基本语法，这就需要一个解读语法的编译程序。这里列出的是一个语法检查函数，主要功能是检查“()”是否配对。实现的基本思想是：规定在脚本语句中可以使用“()”嵌套，则左括号和右括号配对一定是先有左括号，后有右括号，并且在嵌套使用中，左括号允许单个或连续出现，并与将要出现的右括号配对销解，左括号在等待右括号出现的过程中可以暂时保存起来。当右括号出现后，找不到左括号，则发生不配对现象。从程序实现角度讲，左括号连续出现，则后出现的左括号应与最先到来的右括号配对销解。这种左括号的保存和右括号配对销解的过程和栈的“后进先出”原则是一致的。我们可以将读到的左括号压入设定的栈中，当读到右括号时，就和栈中的左括号销解，如果在栈顶弹不出左括号，则表示配对出错，或者当括号串读完，栈中仍有左括号存在，也表示配对出错。大致设计思想如上所述，主要源代码如下：

(1) struct //定义栈结构

{

int St_Data[100]; //数据段

int St_Top; //通常规定栈底 位置在向量低端

} SeqStack;

(2) int Check(SeqStack *stack)//语法检查函数

{

char sz_ch;

int boolean; Push(stack,'# ');

// 压栈，#为判断数据

sz_ch=getchar(); //取值

boolean=1;

while(sz_ch!=' '&&boolean)

{

if(sz_ch= ='(')

Push(stack,ch);

if(sz_ch= =')')

if(gettop(stack)= ='#')

//读栈顶

boolean=0;

else

Pop(stack); //出栈

sz_ch=getchar();

}

if(gettop(stack)!='#') boolean=0;

if(boolean) cout<<"right";

// 输出判断信息

else cout＜＜"error";

以上只介绍了脚本的读取，在下面对图的应用中，再对脚本结构进行深入的研究。总之，凡在游戏中出现先进后出(栈)、先进先出(队列)的情况，就可以运用这两种数据结构，例如《帝国时代》中地表中间的过渡带。

4二叉树的应用

树的应用极其广泛，二叉树是树中的一个重要类型。这里以二叉树的“判定树”为例讲解二叉树的应用，描述分类过程和处理判定优化等方面。

在游戏开发中，通常有很多分类判断。比如：设主角的生命值v，假如在省略其他条件后，有这样的条件判定：当怪物碰到主角后，怪物的反应遵循如下规则：

根据上述条件，可以用如下普通算法来判定怪物的反应：

if(V<100) state=嘲笑，单挑

elseif(V<200)state=单 挑

elseif(V<300) state=嗜血魔法

elseif(V<500) state=呼唤同伴

elsestate=逃跑

上面的算法适用于大多数情况，但时间性能不高，时间复杂度相对较高。我们可以通过判定树来提高其时间性能。首先分析主角生命值的通常特点，即预测出每种条件占总条件的百分比，将这些比值作为权值来构造最优二叉树(哈夫曼树)，作为判定树来设定算法。假设这些百分比为：

构造的哈夫曼树如图2所示。

对应算法如下：

if(V>=200)&&(V<300) state=嗜血魔法

elseif(V>=300)&&(d<500) state=呼唤同伴

else if(V>=100)&&(V<200) state=单挑

else if(V<100) state =嘲笑，单挑

else state =逃跑

通过计算，两种算法的效率比例大约是2:3，很明显，改进的算法在时间性能上提高了不少。一般，在即时战略游戏中，对此类判定算法会有较高的时间性能要求，可以通过二叉树对此进行更深入的研究。

5图的应用

在游戏中，大多数应用图的地方是路径搜索，即A*算法。在此以图的另一种应用为例：在情节脚本中，描述各个情节之间的关系。在游戏中，可能包含很多分支情节，在这些分支情节之间会存在一定的先决条件约束，即有些分支情节必须在其他分支情节完成后方可开始发展，而有些分支情节没有这样的约束。通过以上分析，可以用有向图中的AOV网(Activity On Vertex Network)来描述这些分支情节之间的先后关系。假设有如下的情节：

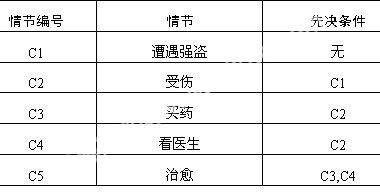
注意：在AOV网中，不应该出现有向环路，否则，顶点的先后关系就会进入死循环。即情节将不能正确发展，可以采取拓扑排序来检测图中是否存在环路。以上情节用图的形式表现如图2所示(此图为有向图，先后关系显示在上面的表格中)：

用邻接矩阵表示此有向图，代码片断如下：

struct Mgraph

{

int Vexs[MaxVex]; //顶点信息

int Arcs[MaxLen][MaxLen]; // 邻接矩阵

……

};

顶点信息存储在情节文件中，将给出的情节表示成邻接矩阵：

0 1 0 0 0

0 0 1 1 0

0 0 0 0 1

0 0 0 0 1

0 0 0 0 0

在此规定，各个情节之间有先后关系，但没有被玩家发展的，用“1”表示；如果情节被发展，就用“2”表示。比如，当已经发展了遭遇强盗的情节，那么，C1与C2顶点之间的关系就可以用“2”表示，注意，这并不表示C2已经被发展，只是表示C2可以被发展了。

请看下面的代码：

class CRelation

{

public:

CRelation(char *filename);

//构造函数，将情节信息文件读入到缓存中

void SetRelation(int ActionRelation);

// 设定此情节已经发展

BOOL SearchRelation(int ActionRelation); // 寻找此情节是否已发展

BOOL SaveBuf(char *filename);

//保存缓存到文件中

……

privated:

char* buf; // 邻接矩阵的内存缓冲

……

};

在这里，我们将表示情节先后关系的邻接矩阵放到缓冲内，通过接口函数修改情节关系，在BOOL SearchRelation (int ActionRelation)函数中，我们可以利用广度优先搜索方法来实现搜索。

我们也可以用邻接链表来表示这个图，但用链表表示会占用更多的内存。邻接链表主要的优点是表示动态的图，在这里并不适合。

参考文献：

[1] 钱能. C++程序设计教程[M]. 北京:清华大学出版社.

[2] 严蔚敏. 数据结构[M]. 北京:清华大学出版社.

[3] 张福炎. 程序员高级程序员程序设计[M]. 北京:清华大学出版社.