Representation of Phase Behavior of Ionic Liquids Using the Equation of State for Square-well Chain Fluids with Variable Range*
LI Jinlong (李进龙), HE Qing (何清), HE Changchun (何昌春), PENG Changjun (彭昌军) and LIU Honglai (刘洪来)
Representation of Phase Behavior of Ionic Liquids Using the Equation of State for Square-well Chain Fluids with Variable Range*
LI Jinlong (李进龙), HE Qing (何清), HE Changchun (何昌春), PENG Changjun (彭昌军)**and LIU Honglai (刘洪来)
State Key Laboratory of Chemical Engineering and Department of Chemistry, East China University of Science and Technology, Shanghai 200237, China
An equation of state (EOS) for square-well chain fluids with variable range (SWCF-VR) developed based on statistical mechanics for chemical association was employed for the calculations of pressure-volume-temperature () and phase equilibrium of pure ionic liquids (ILs) and their mixtures. The new molecular parameters for 23 ILs were obtained by fitting their experimental density data over a wide temperature and pressure ranges. The molecular parameters of ILs composed of homologous organic cation and an identical anion such as [Cmim][NTf2] are good linear with respect to their molecular weight, indicating that the molecular parameters of homologous substances, subsequentlyand vapor-liquid equilibria vapor-liquid equilibria (VLE) can be predicted using the generalized parameter when no experimental data were available. The new set of parameters were satisfactorily used for calculations of the property of solvent and ILs mixture and the solubility of gas in various ILs at low pressure only using one temperature-independent binary interaction parameter.
equation of state, ionic liquids, square-well chain, phase behavior
1 INTRODUCTION
Ionic liquids (ILs) were typically composed of large organic cations and small organic/inorganic anions, and usually considered as a kind of special organic salt. In the past decade, they have received increasing attention due to their promising practice applications in chemistry and engineering such as reaction, separation, catalyzation,[1, 2]. ILs have a wide variety of unique thermophysical properties which include negligible vapor pressure, nonflammability, good thermal and chemical stability, high ionic conductivity, wide liquid region and so on. In particular, the properties of ILs can be artificially tailored for a practical requirement by the right selection of the cation and anion. Therefore, thousands of ILs can be designed and synthesized for specific applications in different fields. In these growing research and utilization, it is necessary to know the physiochemical properties of ILs and their mixtures such as, heat capacity, phase equilibrium,.
The physicochemical and thermodynamic properties of pure ILs and their mixtures have been extensively studiedexperimental methods [3]. In recent years, many theoretical approaches have also been used for the representation of the thermodynamic characteristics and phase behavior of systems containing ILs. The traditional regular solution theory [4], group contribution methods [5], activity coefficient models [6, 7] and cubic equations of state [8] have successfully been applied to model the properties including Henry’s constants, solubilities, liquid-liquid equilibrium,. Several attempts trying to use the SAFT-based models to compute the different thermodynamic properties have been done by different authors. Kroon. [9] modeled ILs as a mixture of two specific components of cations and anions with dipolar interaction, and the pure component parameters of size, energy, association were estimated by literature data, while the segment number parameter was fitted to the experimental density data. Then, they rescaled the pure ionic liquid parameter by fitting the experimentaldata with a wide temperature range and limiting tPC-PSAFT [10] to calculate the phase behavior of ILs at low pressure [11], whereas Andreu and Vega [12] considered ILs as a Lennard-Jones chains with an associating site. The previous studies in our group have shown that ILs can be considered as a square-well chain-like molecule with an associating site or an associating diblock component as well [13-15]. Actually, many studies have indicated that ILs molecules usually exist as ion pairs or cluster and have large sizes, and then, it is reasonable to treat them as chainlike molecules [11-16]. Recently, Wang and coworkers [17] presented an equation of state (EOS) for ILs based on perturbation theory by taking the dispersive and electrostatic interaction into account. In this work, ILs was simply assumed as a chainlike molecule with square-well interaction potential and the pure molecular parameters were obtained by fitting the experimental density data with a wide rang of temperature and pressure. Then, the density and phase equilibrium properties of mixtures containing ILs were predicted and calculated.
2 Brief review of SWCF-VR EOS
In a previous work [18] an equation of state for square-well chain fluid with variable interaction range has been developed on the basis of statistical mechanics for chemical association. In this model a new dispersive contribution to the Helmholtz function for square-well monomers with variable well width range of 1.1≤≤3.0 was established by using the perturbation theory and integral equation approach. Furthermore, the contribution from chain formation was separated into two parts: one is from the hard sphere and the other from the effect of square-well potential. The EOS can well reproduce the compressibility factor and vapor-liquid coexistence curves of pure model fluids and mixtures. It can also be used for the representations ofand VLE for real substances satisfactorily [19-21].
A-component mixture of square-well chains is considered to be comprised ofNchain molecules of component. Each molecule in a mixture is composed ofrtangent spheres with same diametersσ. According to the previous work [18] the residual Helmholtz function and the compressibility factor of a mixture can be written as

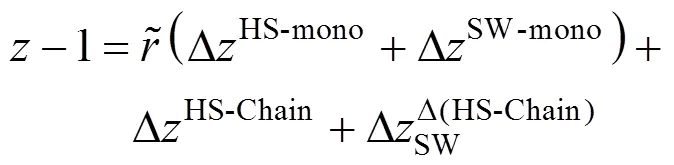
In this EOS each pure non-associating component is characterized by four molecular parameters: segment number per molecule (r), segment diameter (σ), segment-segment interaction energy parameter (ε/) and reduced well width (). These parameters can be obtained by fitting experimental saturated vapor pressure and/or liquid density data of pure fluids [19, 20]. For a mixture the binary energy interaction parameterinεcan be determined from experimental data in order to improve the model accuracy.
3 Results and Discussion
3.1 The molecular parameters and pVT properties of ILs
The EOS is used to correlate the experimental density data with a wide temperature and pressure ranges for pure ILs, and the molecular parameters of segment number (), segment diameter () and dispersion energy (/) are obtained using a simplex method. During the regression, the objective function is based on the minimization of calculated errors of the liquid density

whereNis the experimental point number andis the experimental density data. The superscript “exp” and “cal” denote the experimental and calculated results, respectively. The calculated results and molecular parameters (,3,/) are listed in Table 1 and the overall average deviation of specific volumes and the overall correlation coefficient are 0.07% and 0.9980, respectively. In addition, the range of temperature and pressure, number of data and cited literatures are also given. For all ILs investigated, the optimal reduced well width is fixed as 1.5 as this model can well capture thebehavior of ILs over a wide range of temperature and pressure only using three model parameters.
From Table 1 it is found that the molecular parameters of ILs composed of homologous organic cations and same anions are good linear with respect to their molecular weights (). For instance, the relationships between the numerical values of,3and(/) and molecular weight for the homologous ILs of [Cmim][NTf2] can be fittedlinear functions as follows


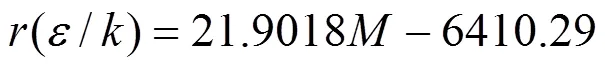

Table 1 Molecular parameters and correlated results of pVT data for ILs (λ1.5)
In the molecular level, the homologous ILs of [Cmim][NTf2] can be regarded as a compound composed of two different groups,.., [Cmim]+and [NTf2]-, in which the anion is identical and the molecular mass only linearly increases with increasing number of carbon atom in cations. In addition, the real molecule in this model is assumed to be composed ofhard sphere segment with diametersurrounded by square-well potentials. The segment number () and the molecular size parameter (3) should increase with increasing molecular weight for homologous series. Thus, it is not surprising that the molecular parameters or their combinations for homologous ILs such as [Cmim][NTf2] linearly increase with increasing molecular mass. Using these generalized model parameters, theproperties and phase behavior of homologous compounds, [Cmim][NTf2], can be predicted even no experimental data is available. The molecular parameters for [C7mim][NTf2] by Eqs. (4)-(6) are obtained without using its experimental density data and the corresponding liquid density is predicted as presented in Fig. 1. The agreement with experiments [31] is satisfactory over a wide temperature and pressure ranges, indicating that this model can be successfully used to predict the thermodynamic propertiesfor some ILs. Furthermore, it is found that the energy parameter between segments of all ILs is larger than that of normal molecules [19, 20]. The reason might be attributed to the fact that there are strong electrostatic interaction between cations and anions in ILs.

Figure 1 Comparison of predicted (line) and experimental [31] (symbols) volumes for [C7mim][NTf2]
/K: 1—293.15; 2—313.15; 3—333.15; 4—353.15; 5—393.15
3.2 Properties of IL mixtures


Figure 2 Comparison of predicted (line) and experimental [32] (symbols) density for [C4mim][PF6](1) + [C4mim][BF4] (2) mixture
Figure 3 Comparison of predicted (line) and experimental[33] (symbols) density for [C4mim][BF4](1) + [C4mim][NTf2] (2) mixture
Phase equilibria for ILs mixtures also require that temperature and pressure of vapor-liquid coexistence phases, and chemical potential of corresponding componentin vapor-liquid mixtures are equal. In fact, ILs have extremely low vapor pressure and the solubility of ILs in vapor phase is very small at equilibria and can be ignored. Thus, the equilibrium equation for binary ILs mixtures at a fixed temperature can be written as
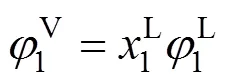

wheremis the number of experimental data points. In calculations, the molecular parameters of normal small molecules were directly gained from our previous work [20].
The temperature-independent binary interaction parametersκand calculated results are listed in Table 2. The overall average relative deviation between calculated and experimental equilibrium pressure and the overall correlation coefficient for all systems are 4.96% and 0.9771, respectively. The average relative deviation of the equilibrium pressure for solvent + ILs systems is 4.53%. For gas + ILs systems at elevated pressure, it is 5.56% with one temperature-independent adjustable binary interaction parameter. It is observed from Table 2 that the differences in the quality of ILs and the experimental methods used by the different researchers could result in a little different value of the adjustable binary interaction parameter and average deviation for the same system, for example, for CO2+ [C4min][PF6] system as shown by Wang[13].

Table 2 The correlated results for solubility of solvents/gases in ILs
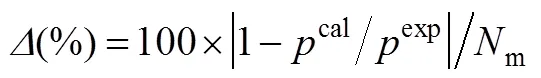


Figure 4 Phase equilibria diagram for CO2(1) + [C4min][PF6] (2) at different temperatures with comparison of this work (solid line) and soft-SAFT (dash line)
/K: 1—283; 2—298; 3—323; 4—348
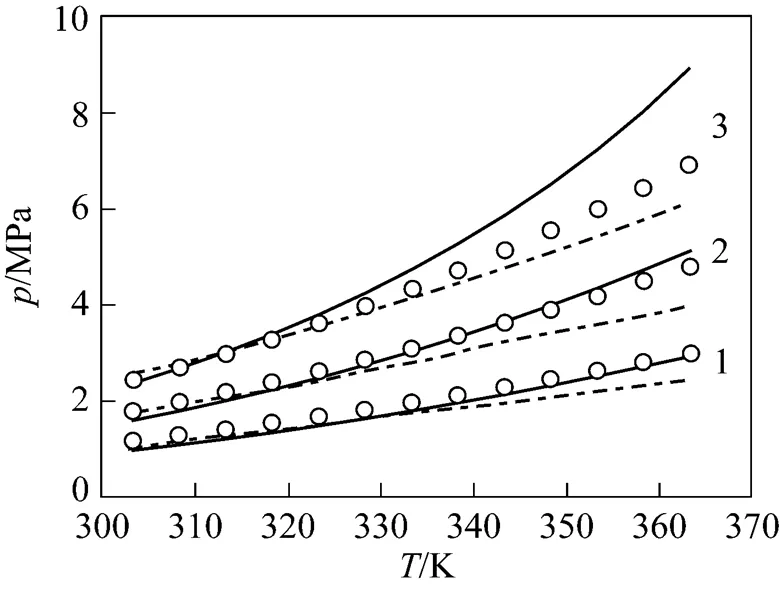
Figure 5-diagram for CHF3(1) + [C4min][PF6](2) at two different mole fraction of CHF3with comparison of this work (solid line) and tPC-PSAFT (dash line)
molar fraction of CHF3: 1—0.203; 2—0.302; 3—0.4

4 Conclusions
In this work, an equation of state for square-well chainlike fluid with variable range was applied to represent theand phase behavior of pure ILs and their mixtures. Both normal fluids and ILs were modeled as a square-well chainlike molecule with dispersion interactions in the EOS. The experimental density data with a wide range of temperature and pressure can be well captured by the model and the average absolute relative deviation is only 0.07%. The new molecular parameters of ILs comprised of homologous cations and an identical anion show good linear relations with respect to molecular weight. Coupled with one-fluid mixture rule, the properties of ILs mixtures were predicted or correlated with one temperature- independent interaction parameter and, in all cases, the results at low pressure were satisfactory.
1 Cole-Hamilton, D.J., “Homogeneous catalysis—new approaches to catalyst separation, recovery and recycling”,, 299, 1702-1706 (2003).
2 Chu, X., Hu, Y., Li, J., Liang, Q., Liu, Y., Zhang, X., Peng, X., Yue, W., “Desulfurization of diesel fuel by extraction with [BF4]-based ionic lquids”,...., 16, 881-884 (2008).
3 Heintz, A., “Recent developments in thermodynamics and thermophysics of non-aqueous mixtures containing ionic liquids. A review”,..., 37, 525-535 (2005).
4 Scovazzo, P., Camper, D., Kieft, J., Poshusta, J., Koval, C., Noble, R., “Regular solution theory and CO2gas solubility in room temperature ionic liquids”,...., 43, 6855-6860 (2004).
5 Wang, J., Sun, W., Li, C., Wang, Z., “Correlation of infinite dilution activity coefficient of solute in ionic liquid using UNIFAC model”,., 264, 235-241 (2008).
6 Huo, Y., Xia, S., Yi, S., Ma, P., “Measurement and correlation of vapor pressure of benzene and thiophene with [Bmim][PF6] and [Bmim][BF4] ionic liquids”,., 276, 46-52 (2009).
7 Jiang, X., Zhao, S., Sun, X., Fu, D., “Phase equilibrium of ionic liquids and high boiling point aromatic compounds”,...., 58 (4), 818-821 (2007). (in Chinese)
8 Carvalho, P.J., Álvarez, V.H., Machado, J.J.B., Pauly, J., Daridon, J.L., Marrucho, I.M., Aznar, M., Coutinho, J.A.P., “High pressure phase behavior of carbon dioxide in 1-alkyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ionic liquids”,.., 48, 99-107 (2009).
9 Kroon, M.C., Karakatsani, E.K., Economou, I.G., Witkamp, G.J., Peters, C.J., “Modeling of the carbon dioxide solubility in imidazolium-based ionic liquids with the tPC-PSAFT equation of state”,..., 110, 9262-9269 (2006).
10 Karakatsani, E.K., Economou, I.G., “Pertured chain statistical associating fluid theory extended to dipolar and quardrupolar molecular fluids”,..., 110, 9252-9261 (2006).
11 Karakatsani, E.K., Economou, I.G., Kroon, M.C., Peters, C.J., Witkamp, G.J., “tPC-PSAFT modeling of gas solubility in imidazolium-based ionic liquids”,..., 111, 15487-15492 (2007).
12 Andreu, J.S., Vega, L.F., “Capturing the solubility behavior of CO2in ionic liquids by a simple model”,..., 111, 16028-16034 (2007).
13 Wang, T.F., Peng, C.J., Liu, H.L., Hu, Y., “Description of thebehavior of ionic liquids and the solubility of gases in ionic liquids using an equation of state”,., 250, 150-157 (2006).
14 Wang, T.F., Peng, C.J., Liu, H.L., Hu, Y., Jiang, J.W., “Equation of state for the vapor-liquid equilibria of binary systems containing imidazolium-based ionic liquids”,...., 46, 4323-4329 (2007).
15 Geng, Y.F., Wang, T.F., Yu, D.H., Peng, C.J., Liu, H.L., Hu, Y., “Densities and viscosities of the ionic liquid [C4mim][PF6] +,-dimethylformamide binary mixtures at 293.15 K to 318.15 K”,...., 16, 256-262 (2008).
16 Del Popolo, M.G., Voth, G.A., “On the structure and dynamics study of ionic liquids”,..., 108, 1744-1752 (2004).
17 Wang, J., Li, C., Shen, C., Wang, Z., “Towards understanding the effect of electrostatic interactions on the density of ionic liquids”,., 279, 87-91 (2009).
18 Li, J.L., He, H.H., Peng, C.J., Liu, H.L., Hu, Y., “A new development of equation of state for square-well chain-like molecules with variable width 1.1≤≤3”,., 276, 57-68 (2009).
19 Li, J.L., Peng, C.J., Liu, H.L., “Modeling vapor-liquid equilibrium of refrigerants using an equation of state for square well chain fluid with variable range”,......, 60, 545-552 (2009). (in Chinese)
20 Li, J.L., He, H.H., Peng, C.J., Liu, H.L., Hu, Y., “Equation of state for square-well chain-like molecules with variable range (I) Application for pure substances”,., 286, 8-16 (2009).
21 Li, J.L., Tong, M., Peng, C.J., Liu, H.L., Hu, Y., “Equation of state for square-well chain-like molecules with variable range (II) Extension to mixtures”,., 287, 50-61 (2009).
22 Esperanca, J.M.S.S., Guedes, H.J.R., Blesic, M., Rebelo, L.P.N., “Densities and derived thermodynamic properties of ionic liquids (3) Phosphonium-based ionic liquids over and extended pressure range”,..., 51, 237-242 (2006).
23 Machida, H., Sato, Y., Smith, Jr. R.L., “Pressure-volume-temperature () measurements of ionic liquids ([bmim+][PF6-], [bmim+][BF4-], [bmim+][OcSO4-]) and analysis with the Sanchez-Lacombe equation of state”,., 264, 147-155 (2008).
24 Gardas, R.L., Freire, M.G., Carvalho, P.J., Marrucho, I.M., Fonseca, I.M.A., Ferreira, A.G.M., Coutinho, J.A.P., “High pressure densities and derived thermodynamic properties of imidazolium-based ionic liquids”,..., 52, 80-88 (2007).
25 Krummen, M., Wasserscheid, P., Gmehling, J., “Measurement of activity coefficients at infinite dilution in ionic liquids using the dilutor technique”,..., 47, 1411-1417 (2002).
26 Hofman, T., Goldon, A., Nevines, A., Letcher, T.M., “Densities, excess volumes, isobaric expansivity, and isothermal compressibility of the (1-ethyl-3-methylimidazolium ethylsulfate + methanol) system at temperatures (283.15 to 333.15) K and pressure from (0.1 to 35) MPa”,..., 40, 580-591 (2008).
27 Fredlake, C.P., Crosthwaite, J.M., Hert, D.G., Aki, S.N.V.K., Brennecke, J.F., “Thermophysical properties of imidazolium-based ionic liquids”,.., 49, 954-964 (2004).
28 Esperanca, J.M.S.S., Visak, Z.P., Plechkova, N.V., Seddon, K.R., Guedes, H.J.R., Rebelo, P.N., “Density, speed of sound, and derived thermodynamic properties of ionic liquids over and extender pressure range (4) [C3min][NTf2] and [C5min][NTf2]”,..., 51, 2009-2015 (2006).
29 Azevedo, R.G., Esperanca, J.M.S.S., Szydlowski, J., Visak, Z.P., Pires, P.F., Guedes, H.J.R., Rebelo, L.P.N., “Thermophysical and thermodynamic properties of ionic liquids over an extended pressure range: [bmim][ NTf2] and [hmim][ NTf2]”,..., 37, 888-899 (2005).
30 Kato, R., Gmehling, J., “Systems with ionic liquids: Measurement of VLE and data and prediction of their thermodynamic behavior using original UNIFAC, mod. UNIFAC(Do) and COSMO-RS(Ol)”,..., 37, 603-619 (2005).
31 Gardas, R.L., Freire, M.G., Carvalho, P.J., Marrucho, I.M., Fonseca, I.M.A., Ferreira, A.G.M., Coutinho, J.A.P., “measurements of imidazolium-based ionic liquids”,..., 52, 1881-1888 (2007).
32 Navia, P., Troncoso, J., Romani, L., “Excess magnitudes for ionic liquid binary mixtures with a common ion”,..., 52, 1369-1374 (2007).
33 Lopes, J.N.C., Cordeiro, T.C., Esperanca, J.M.S.S., Guedes, H.J.R., Huq, S., Rebelo, L.P., Seddon, K.R., “Deviations from ideality in mixtures of two ionic liquids containing a common ion”,..., 109, 3519-3525 (2005).
34 Kato, R., Gmehling, J., “Measurement and correlation of vapor-liquid equilibria of binary systems containing the ionic liquids [EMIM][(CF3SO2)2N], [BMIM] [(CF3SO2)2N], [MMIM][(CH3)2PO4] and oxygenated organic compounds respectively water”,., 231, 38-43 (2005).
35 Kato, R., Krummen, M., Gmehling, J., “Measurement and correlation of vapor-liquid equilibria and excess enthalpies of binary systems containing ionic liquids and hydrocarbons”,., 224, 47-54 (2004).
36 Verevkin, S.P., Safarov, J., Bich, E., Hassel, E., Heintz, A., “Thermodynamic properties of mixtures containing ionic liquids vapor pressures and activity coefficients of-alcohols and benzene in binary mixtures with 1-methyl-3-butyl-imidazolium bis(trifluoromethyl-sulfonyl) imide”,., 236, 222-228 (2005).
37 Safarov, J., Verevkin, S.P., Bich, E., Heintz, A., “Vapor pressures and activity coefficients of-alcohols and benzene in binary mixtures with 1-methyl-3-butyl-imidazolium octyl sulfact and 1-methyl-3-butyl- imidazolium tetrafluoroborate”,..., 51, 518-525 (2006).
38 Nebig, S., Bolts, R., Gmehling, J., “Measurement of vapor-liquid equilibria (VLE) and excess enthalpies (HE) of binary systems with 1-alkyl-3-methylimidazolium bis(trifluoromethylsulfonyl) imide and prodiction of these properties and∞using modified UNIFAC (Dortmund)”,., 258, 168-178 (2007).
39 Kim, Y.S., Choi, W.Y., Jang, J.H., Yoo, K.P., Lee, C.S., “Solubility measurement and prediction of carbon dioxide in ionic liquids”,., 228/229, 439-445 (2005).
40 Kroon, M.C., Shariati, A., Costantini, M., Spronsen, J., Witkamp, G.J., Sheldon, R.A., Peters, C.J., “High pressure phase behavior of systems with ionic liquids (V) The binary system carbon dioxide + 1-butyl-3-methylimidazolium tetrafluoroborate”,..., 50, 173-176 (2005).
41 Lee, B.C., Outcalt, S.L., “Solubilities of gases in the ionic liquid 1--butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide”,..., 51, 892-897 (2006).
42 Kamps, A.P.S., Tuma, D., Xia, J., Maurer, G., “Solubility of CO2in the ionic liquid [bmim][PF6]”,..., 48, 746-749 (2003).
43 Shariati, A., Gutkowski, K., Peters, C.J., “Comparison of the phase behavior of some selected binary systems with ionic liquids”,., 51, 1532-1540 (2005).
44 Zhang, S., Yuan, X., Chen, Y., Zhang, X., “Solubility of CO2in 1-butyl-3-methylimidazolium hexafluorophosphate and 1,1,3,3-tetramethylguanidium lactate at elevated pressures”,..., 50, 1582-1585 (2005).
45 Shariati, A., Peters, C.J., “High pressure phase behavior of systems with ionic liquids (III) The binary system carbon dioxide + 1-hexyl-3-methylimidazolium hexafluorophosphate”,., 30, 139-144 (2004).
46 Aki, S.N.V.K., Mellein, B.R., Saurer, E.M., Brennecke, J.F., “High pressure phase behavior of carbon dioxide with imidazolium-based ionic liquids”,..., 108, 20355-20365 (2004).
47 Shiflett, M.B., Yokozeki, A., “Solubilities and diffusivities of carbon dioxide in ionic liquids: [bmim][PF6] and [bmim][BF4]”,...., 44, 4453-4464 (2005).
2009-06-22,
2009-10-14.
the National Natural Science Foundation of China (20876041, 20736002), the National Basic Research Program of China (2009CB219902), Program for Changjiang Scholars and Innovative Research Team in University of China (IRT0721) and the 111 Project of China (B08021).
** To whom correspondence should be addressed. E-mail: cjpeng@ecust.edu.cn
 Chinese Journal of Chemical Engineering2009年6期
Chinese Journal of Chemical Engineering2009年6期
- Chinese Journal of Chemical Engineering的其它文章
- Effect of Working Temperature on the Resistance Characteristic of aPleated Stainless Steel Woven Filter*
- The Numerical Simulation of Collapse Pressure and Boundary of the Cavity Cloud in Venturi*
- Performance of Inner-core Supersonic Gas Separation Device with Droplet Enlargement Method*
- Void Fraction Distributions in Cold-gassed and Hot-sparged Three Phase Stirred Tanks with Multi-impeller*
- Kinetics of COD Removal in a Biological Aerated Filter in thePresence of 2,4,6-Trinitrophenol (Picric Acid)*
- Proton-exchange Sulfonated Poly(ether ether ketone)/SulfonatedPhenolphthalein Poly(ether sulfone) Blend Membranes in DMFCs*
