Suppression of ice nucleation in supercooled water under temperature gradients

Li-Ping Wang(王利平), Wei-Liang Kong(孔维梁), Pei-Xiang Bian(边佩翔), Fu-Xin Wang(王福新), and Hong Liu(刘洪)

School of Aeronautics and Astronautics,Shanghai Jiao Tong University,Shanghai 200240,China

Keywords: supercooled water,ice nucleation,temperature gradient,thermodynamic analysis,classical nucleation theory

1. Introduction

The supercooling and freezing of water generally occur in nature and have significant impact on human activities with various types in numerous important areas such as aviation safety, food and biological sample preservation, global climate change, wind turbines, power transmission lines and so on.[1–7]The water can remain liquid at temperatures of about−40◦C and the occurrence of spontaneous nucleation of ice at slightly cold temperatures has been regarded as homogeneous nucleation.[8,9]At higher temperatures,whether water freezes is determined by heterogeneous ice nucleation.[5]The foreign substances, such as impurities[10]and surface contact,[11]are commonly considered as the main factors for heterogeneous ice nucleation. Its efficiency can be regulated through ion exchange,[12]and the depression and promotion effects of antifreeze proteins on it can be achieved via selectively binding the ice-binding face and the non-ice-binding face of antifreeze proteins to solid substrates.[13]It has been proved that the behaviors of nucleation can also be affected by a variety of external perturbations such as pressure,mechanical stimulus,flows,electric and magnetic fields and so on.[14–21]Temperature as a decisive factor for nucleation,[22,23]if there are fluctuations or gradients, is deemed to be a thermal disturbance to influence the stability of supercooled water.[24]Meanwhile,the temperature differences are actually present in some practical applications.For instance,the supercooled drop is quickly prepared from room temperature water or the supercooled preservation of biological samples are exposed in warm environment.[24–26]Therefore,it is necessary and meaningful to get more knowledge about how temperature gradient affects ice nucleation.

Nucleation is a process of formation of a thermodynamically stable daughter phase from a metastable parent phase.To perceive nucleation, one should proceed from the classical nucleation theory (CNT) formulated in the first half of the twentieth century, which is phenomenological and describes the formation and propagation of clusters of the daughter phase within the parent phase. In CNT, there is a fundamental assumption called capillarity approximation,of which the essence is that a cluster is viewed as a liquid drop or solid particle of a well-defined radius with the bulk properties of the nucleated phase. In addition, the surface energy of the cluster is presented as the product of the surface area of the cluster and the planar interfacial tension at a uniform temperature.[27]Similarly, this is a well-defined temperature generally set equal to the temperature of the surrounding parent phase bath or the foreign contact for computing cluster properties.[28]In the case of temperature gradients, the temperature is used as the minimum measured temperature.

Studies of non-isothermal nucleation have paid attention to the temperature fluctuations on the cluster caused by evaporation, molecular absorption and collision, etc. and proved that such fluctuations have a significant effect on the nucleation rate.[28–30]Cao and Yang have developed a temperaturedependent nucleation theory to elucidate the heterogeneous nucleation process by considering the thermal fluctuations of the nucleus surface based on CNT and founded that the critical energy barrier with thermal fluctuations was smaller than that without it.[31]However,these results have not reflected the influence of thermal disturbance at macroscopic scale, such as the temperature fluctuations and gradients within the bath,on nucleation.

To investigate nucleation in a temperature gradient,Reguera and Rubi have analyzed nucleation phenomena in inhomogeneous media with low thermal conductivity,which favors the development of very large temperature gradients.[32]Their results showed that the nucleation process can be drastically affected by the presence of a large temperature gradient.It has been founded that the plane of recrystallized thin Si films can be controlled by adjusting temperature gradients through molecular-dynamics simulations.[33]Researches above do not involve temperature-gradient effects on the initiation of nucleation. Okawaet al.have calculated the probability of freezing per unit surface area per unit time internal in studying the effect of cooling rate on freezing of supercooled water.[34]They found the probability was independent of the cooling rate. Huanget al.[24]have experimentally studied the stability of deep-supercooled water under thermal disturbances induced by plunging the samples into 37◦C water bath or putting them into 37◦C incubator. However, the frozen samples are very few. Even so, it cannot be explained that the temperature gradients will not affect the nucleation temperature due to the transient and instability temperature difference in their experiments.

A higher cooling rate can lower the freezing temperature whether for droplet or water with a certain volume.[34–36]In our previous study, we have carried out water freezing experiments to measure nucleation temperature under different temperature differences.[37]The median nucleation temperature is about−16.3◦C during isothermal cooling, but it is−20.1◦C by unilaterally cooling the water initially at an equilibrium state of−5◦C. When nucleation occurs, the median temperature at one side of the supercooled water is the nucleation temperature−20.1◦C and the average temperature at the other side is−6.8◦C.The results showed that the degree of supercooling needed to trigger nucleation in temperature gradients is larger than that in isothermal conditions. Meanwhile,we found that the temperature gradient possibly changes the free energy barrier for nucleation according to the evaluation of nucleation rate. From the perspective of these macroscopic experimental phenomena, the temperature difference will affect the nucleation and freezing behavior. At the nano/micro scale, what is the nucleation behavior in non-isothermal conditions. In CNT, both the driving thermodynamic force for nucleation and the interfacial energy between phases are temperature dependence.[38,39]Any change in temperature distribution on cluster will inevitably change free energy. In recent years, various researches have developed a bubble nucleation model in temperature gradient based on free energy analysis[40,41]to improve the estimation of nucleation barrier,which is a more recognized and effective method to achieve the most important corrections to CNT,[42]but to the best of our knowledge, the related models on ice nucleation are still absent. The present paper focuses on the development of nucleation model in a temperature gradient based on CNT by estimating the change in free energy barrier due to the presence of temperature distribution in cluster.

2. A brief review on classical nucleation theory

2.1. Free energy barrier

In CNT,in order to perform phase transition, the system has to overcome a free energy barrier ∆G∗,which reflects the competition between the energy cost and energy gain in the process of formation of the new phase called nucleus.[27,43,44]The former is associated with the creation of a new surface between phases and destabilizes the nuclei, denoted as surface or interface free energy ∆Gsurf,and the latter is associated with bulk energy of phase transition and stabilizes the nuclei,denoted as the volumetric free energy ∆Gvol.[17,45,46]Thus,the change in free energy,also called Gibbs free energy of cluster formation,during homogeneous nucleation to form a spherical ice embryo with radiusrcan be given as[17,39]

whereAiandViare the surface area and volume of ice embryo,respectively,γiwis the ice–water interfacial energy,which can be expressed as[38]

with unit of mJ/m2in the temperature range from 237.15 K to 273.15 K,and ∆Gvis the volumetric free energy difference per unit volume between ice and water,which is given by the equation as follows forT ＜Tm:

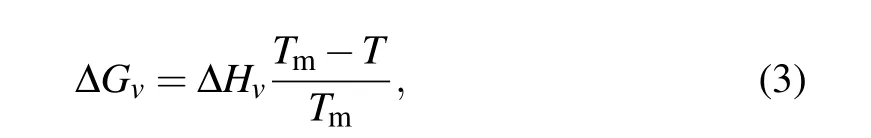
where ∆Hv=287 MJ/m3is the water volumetric enthalpy of fusion andTm=273.15 K is the ice melting temperature.

For a very small nucleus, the surface free energy dominates and a metastable state is maintained; while as the nucleus grows torc, the volumetric free energy gain will eventually overcome the surface free energy cost, at the moment the formation free energy for a nucleus reaches a maximum∆G∗, and then nucleation is triggered and ice grows spontaneously,as shown in Fig.1. As a result,differentiating Eq.(1)with respect torand setting it to zero,the critical radiusrcfor nucleation can be determined as

and the free energy barrier for homogeneous nucleation can be determined by substituting Eq.(4)into Eq.(1)to give

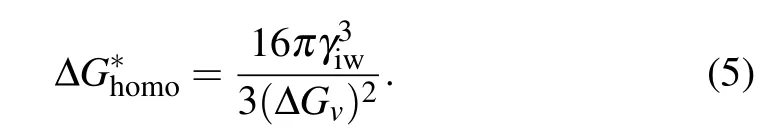
For heterogeneous nucleation, the free energy barrier to form the critical nucleus is expressed as[27,47]

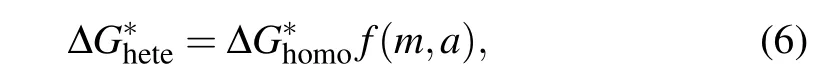
where the functionfis the Fletcher factor,[47]which varies between 0 to 1 and depends on the Young’s contact angleθof nucleus(cluster)on the foreign particle(underlying surface)in supercooled water and the relative sizeaof foreign particles with respect to the nucleus. It can be expressed as

Generally,the flat geometry limit can be applied whena ＞10.

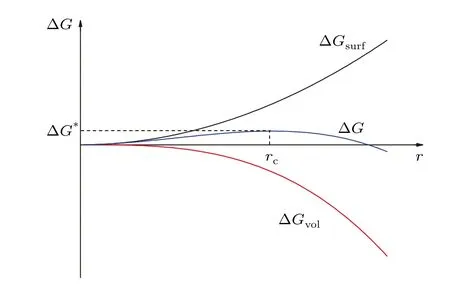
Fig. 1. Plot of the nucleation barrier for nucleus formation resulting from the competition between the surface and the volume free energies.

2.2. Nucleation rate

In CNT,a temperature-dependent nucleation rate was developed to describe the nucleation process, which contains a kinetic and a thermodynamic component.[35]The steady state homogeneous and heterogeneous nucleation rate for supercooled water can be respectively expressed as[35,38,48]

3. Nucleation under temperature gradients

In this section, we will make corrections in the frame of CNT to achieve the improved estimates of the change in free energy for nucleus formation with the consideration of temperature gradient. First, we assume that the liquid water is between two infinite substrates and there is a temperature difference between them. In the presence of cooled substrate,the ice embryo generally forms via heterogeneous nucleation at the water-substrate interface and starts at the low-temperature area because the nucleation rate increases exponentially as the temperature decreases. In the heterogeneous nucleation case,the ice embryo is on the condensation nuclei and thus there is a three-phase contact line, which can be characterized by the Young’s contact angleθmentioned in Subsection 2.1. What’s more,the condensation nuclei are treated as a perfectly smooth planar macroscopic surface in our analysis.

It is well known that there are temperature discontinuities at the interfaces (ice/water–substrate and ice–water) due to the interfacial thermal resistance.[54,55]In addition,the thermal fluctuation of the ice–water interface on the nanoscale caused by evaporation and absorption of water molecules will result in the change in cluster temperature.[28,31]As a result,the actual temperature distribution in the cluster and inside the metastable supercooled state is extremely complicated.[56]The aim of this paper is to study whether or how the existence of temperature gradient affects nucleation behavior. So the actual profile of temperature distribution will not be the main concern. To estimate the change in free energy under the influence of temperature gradient in a simplified and feasible method, we refer to the analytical method used in bubble nucleation on the heated surface[40,57]and make the following assumptions:

1. The system is in a non-equilibrium steady state and the temperature distribution within water between the two substrates is linear. In addition, the temperature at the water/ice-substrate interface is continuous, i.e.,Ti=Tw=Tsatx=0. Here,Tiis the temperature in the ice nucleus,Twis the temperature in water,Tsis the temperature of the cooled substrate andxis the distance from the cooled substrate.

2. The heat is strictly transferred parallel to thex-axis from positive to negative directions indicating that the ice–water interface is in thermal equilibrium at the same distancexfrom the cooled substrate.Thus,the temperature within the ice nucleusTi(x)is considered to be equal to the temperature within waterTw(x),i.e.,

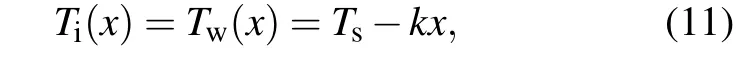
wherekis the temperature gradient and negative in our analysis. Note that negative just means direction, not magnitude.

3. Even though the ice–water interfacial energies are different at the different positions on the ice nucleus due to the temperature difference,the spherical shape of the ice embryo and the contact angleθwill not change.

Figure 2 schematically shows this configuration and the temperature profiles of the ice nucleus and the bulk water. It should be noted that another substrate with higher temperature at the far end is not demonstrated in the schematic diagram.

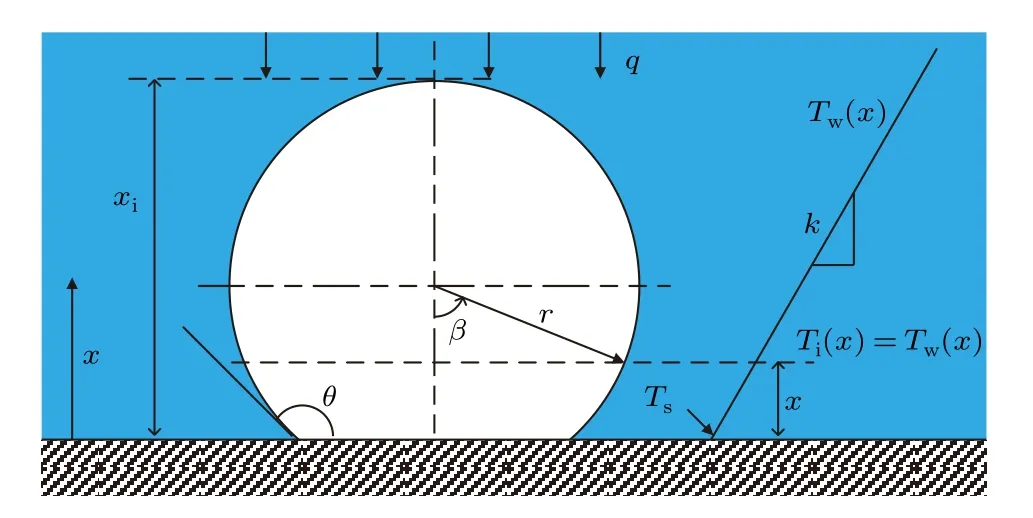
Fig. 2. Schematic of ice embryo on substrate and the temperature distributions in ice embryo/cluster and bulk water.

The ice embryo is resting on the surface resulting in an additional interface between it and the substrate compared the homogeneous case.Hence,the surface contribution to free energy for heterogeneous nucleation includes two aspects and is given as[27]

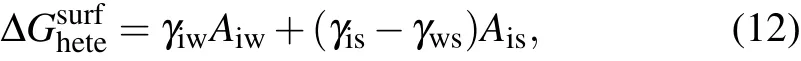
whereγisandγwsare the interfacial energies between ice and substrate and between water and substrate, respectively.AiwandAisare the corresponding areas between the phases. The second term ascribes to the water–surface interface replaced by the ice–surface interface. Given the mechanical equilibrium among the phases,the relationship among the interfacial forces at the three-phase contact line can be expressed as

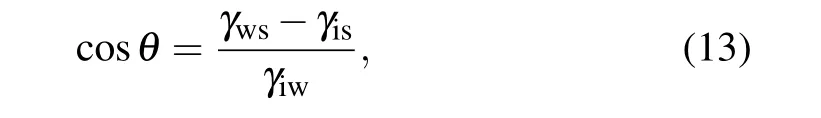
which is known as Young’s equation. The ice nucleus temperatureTi(x) given by Eq. (11) is a function ofxin the nucleus. To evaluate the change in free energy in the formation of ice embryo, an integral on surface and volumetric free energy with respect toxfromx=0 tox=xishould be made.xi=r(1−cosθ) is the height of ice embryo. Substituting Eq.(13)into Eq.(12),and considering a constant temperature of the substrate for one case and the temperature dependence of ice–water interfacial energy given by Eq. (2), we can obtain the surface free energy for heterogeneous nucleation in temperature gradient as follows:

It should be noted that the second term in Eq. (14) is independent of temperature gradient and just determined by the temperature of substrate and the Young’s contact angle. And the volumetric free energy can be expressed as

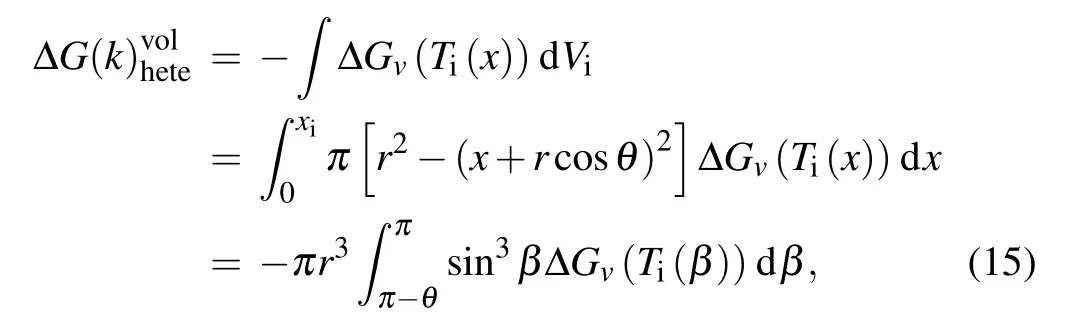
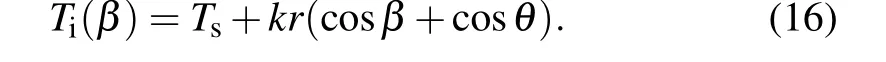
whereβis the angle between the radial of the nucleus and negativex-axis. Temperature distribution within the nucleus inβcan be expressed as Substituting Eq.(16)into Eqs.(2)and(3)respectively to obtain the expressions forγiwand ∆Gvwith respect toβ, and then substituting them into Eqs. (14) and (15) respectively to give

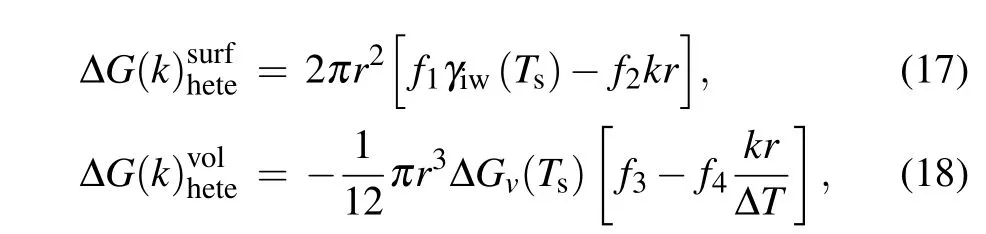
wheref1=1−cosθ −(1/2)sin2θcosθ,f2=(1/8000)(1−cosθ)2,f3=4cos3θ −12cosθ+8,f4=cos4θ −6cos2θ+8cosθ −3. ∆T=Tm−Tsis the maximum degree of supercooling of water in the system. As a result,the change in free energy for formation of a nucleus of radiusrwith the Young’s contact angleθduring heterogeneous nucleation in temperature gradientkcan be expressed as

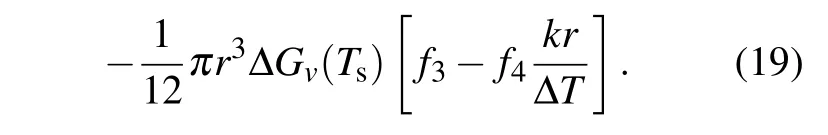
As mentioned in Subsection 2.1,the maximum change in free energy is the energy barrier for nucleation. Thus,the critical radius for heterogeneous nucleation in temperature gradient can be determined by making the derivation of Eq. (19)with respect torequal to zero, which gives the equation as follows:

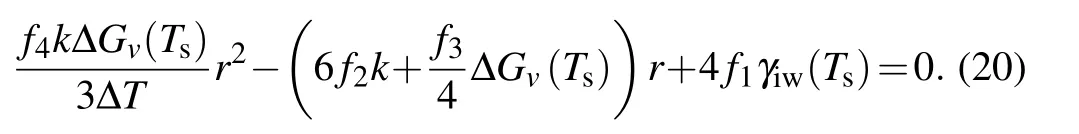
For nucleation at equilibrium conditions, i.e., for the case ofk=0,we can obtain

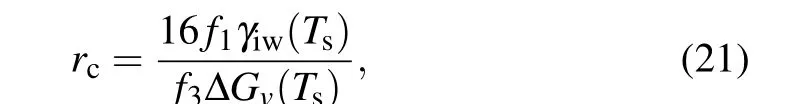
which reduces to Eq.(4)for nucleation in CNT as 16f1/f3is a constant 2 forθin the range of 0 toπ. When there is a temperature gradient(k/=0),solving Eq.(20),and considering the actual scale of ice nuclei and the relationship with the degree of supercooling,we can obtain

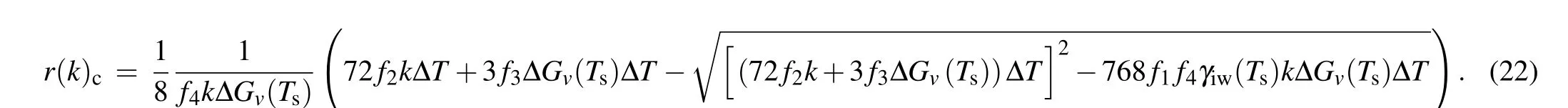
Note that to ensure that Eq.(20)has real roots,it needs

Although our analysis on the nucleation barrier in a temperature gradient is based on the heterogeneous nucleation,if we setθ=π,it will become a homogeneous nucleation.Thus,we will not discuss homogeneous nucleation in temperature gradient in a separate case in the next, but incorporate it into the heterogeneous nucleation in a form ofθ=πas needed.

4. Results and discussion

4.1. The change in free energy

Through the above analysis, we can see that a suitable temperature gradient,or temperature difference within the nucleus,will change the energy cost(see Eq.(18))and the energy gain(see Eq.(18))in the process of an ice embryo formation to affect the change in free energy. Figure 3 shows the variations of the surface free energy,the volumetric free energy and the change in free energy to form an ice embryo with radiusrin different temperature gradients at the degree of supercooling ∆T=15◦C and contact angleθ=180◦. The calculated results show that the temperature gradient will increase the energy cost to form the interface between phases during the formation of nucleus but decrease the energy gain due to phase transition compared to the case in uniform temperature. However,the change in the volumetric free energy is more obvious than the change in the surface free energy. Thus,an increased Gibbs free energy and a larger critical radius of nucleus is needed to trigger nucleation under temperature-gradient conditions. The critical radius will increase as the temperature gradient increases. However, when the temperature gradient increases to a critical value,even for a large nucleus,the volumetric free energy gain can no longer overcome the surface free energy cost, as shown in Fig. 3(c). Therefore, the nucleation barrier will continue to increase as the nucleus radius increases resulting in an ice embryo that will not grow spontaneously. Consequently, the ice nucleation will be completely suppressed. In this paper, we define this critical value as the critical temperature gradientkc,which will be demonstrated in Subsection 4.3.

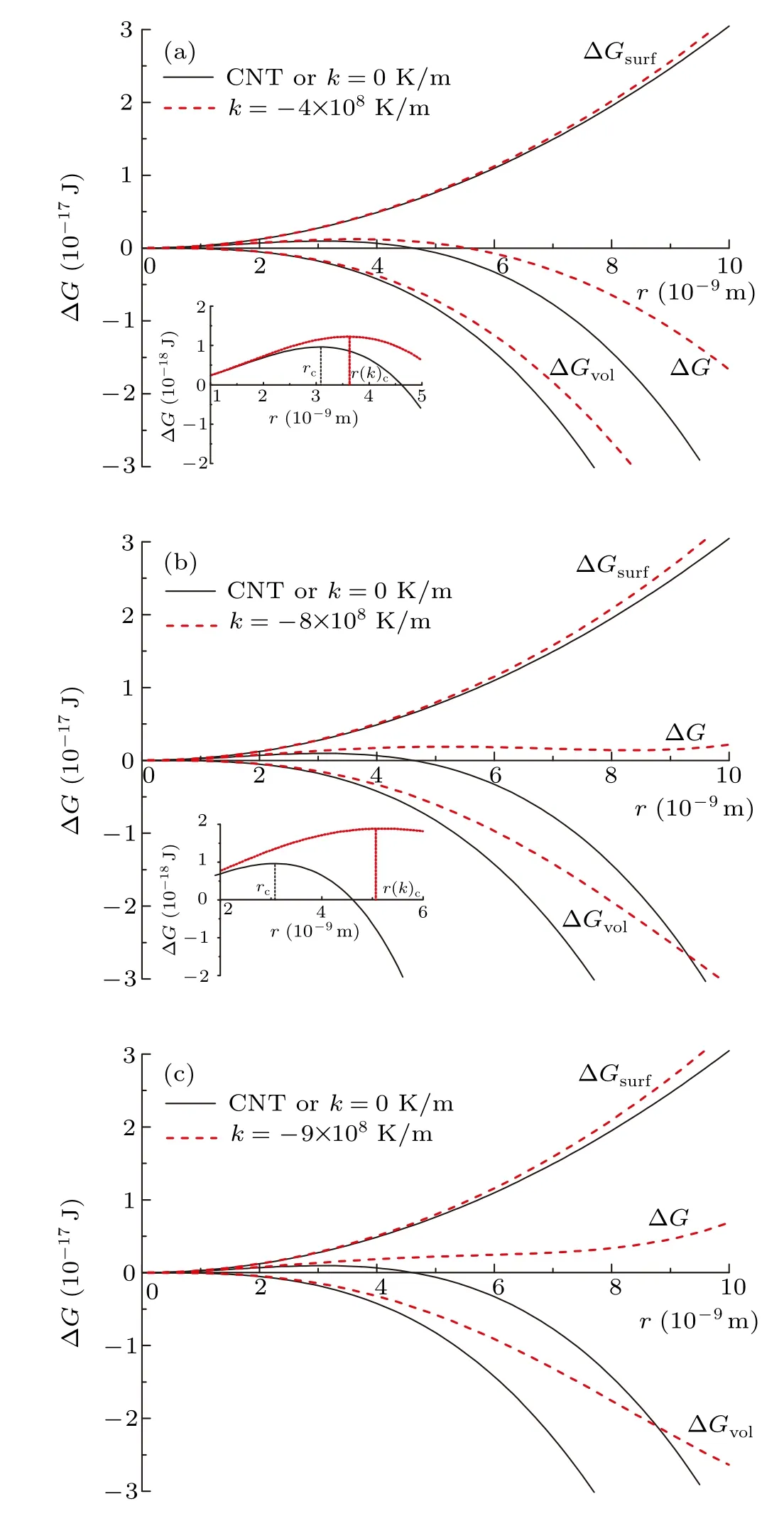
Fig.3. Variations of the surface free energy,the volumetric free energy and the change in free energy of cluster formation with radius of ice embryo r in different temperature gradients at ∆T =15 ◦C and contact angle θ =180◦.(a)k=−4×108 K/m;(b)k=−8×108 K/m;(c)k=−9×108 K/m.

4.2. Critical radius of ice nucleus for nucleation

In CNT,whether the radius of an ice embryo reaches the critical radius determines whether it continues to grow or to disappear. Thus, it is important to acquire the critical radius.In the previous subsection,it is found that the critical nucleus radius can be changed by an appropriate temperature gradient.What is the threshold value and does it have the same effect under different degrees of supercooling.

Figure 4 shows the relationship between the critical nucleus radius and the degree of supercooling in different temperature gradients with contact angleθ=180◦. The most obvious presentation is that the change in the critical radius affected by temperature gradient is more significant at a low degree of supercooling than that at a high degree of supercooling,regardless of the magnitude of temperature gradient. Furthermore, we can see that when the temperature gradient reaches−107K/m, the critical nucleus radius begins to increase at a low degree of supercooling and the influence is negligible in the case of the degree of supercooling larger than 5◦C. For a larger temperature gradient, the critical radius will increase more significantly,but the change is still minor at a high degree of supercooling. In addition,it is more important to note that there will be no critical nucleus radius at the low degree of supercooling for a large enough temperature gradient, meaning that the nucleation will not be induced spontaneously. Thus,there is a critical temperature gradient for a given degree of supercooling,at the higher of which the ice nucleation will be completely suppressed.

Fig. 4. The critical radius as a function of the degree of supercooling in different temperature gradients with contact angle θ =180◦.

The contact angle between the cluster and the condensation nuclei plays an important role in the process of heterogeneous nucleation.[58]It is well known that the critical radius of the ice embryo in CNT is independent of the condensation nuclei and does not change as the contact angle changes.[27,47]However, in our analysis, when a temperature gradient is applied,the critical radius is not only dependent on the temperature gradient but also on the contact angle under the competition of surface free energy and volumetric free energy to reach the nucleation barrier,as demonstrated in Eq.(22).

Figure 5 shows the variations of the critical radius with the degree of supercooling at various contact angles in a fixed temperature gradient−4×108K/m. Similarly,it can be seen that the influence of contact angle is more apparent at the low degree of supercooling. In addition, as the contact angle increases, the change in the critical radius is more significant and the supercooling area that cannot spontaneously nucleate will increase. That is to say the contact angle will affect the critical temperature gradient for a given degree of supercooling.

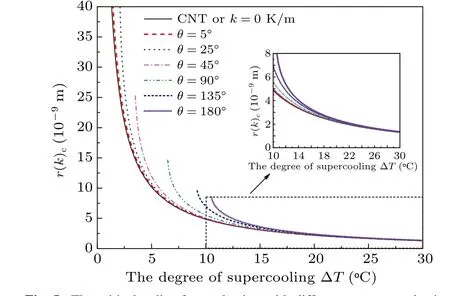
Fig. 5. The critical radius for nucleation with different contact angles in a given temperature gradient −4×108 K/m.

Whether the temperature gradient or the contact angle affects the critical radius, the change is more obvious at a low degree of supercooling. The reason can be attributed to the fact that the volumetric free energy is proportional to the degree of supercooling (see Eq. (3)); its relative change caused by the temperature gradient is greater at the low degree of supercooling than that at the high degree of supercooling.

4.3. Critical temperature gradient

As presented in the above section,for a given contact angle,there will be a corresponding critical temperature gradient for each degree of supercooling. Reviewing Eq. (23), it can be considered that its physical interpretation is to ensure that the volumetric free energy can eventually overcome the surface free energy. Thus,the critical temperature gradientkccan be determined by setting Eq.(23)equal to zero to give

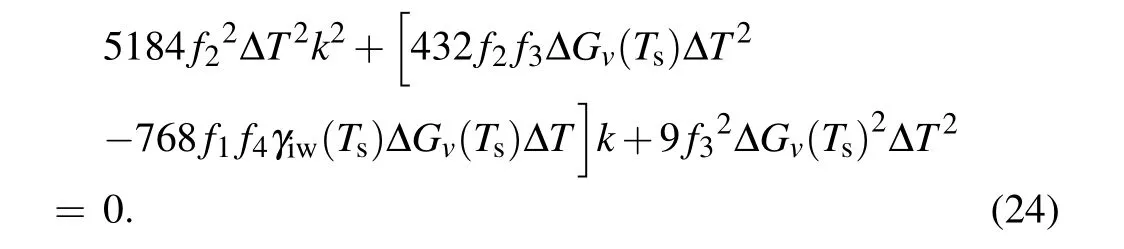
Solving Eq. (24) and considering the approximate value as mentioned earlier, the critical temperature gradientkccan be given as

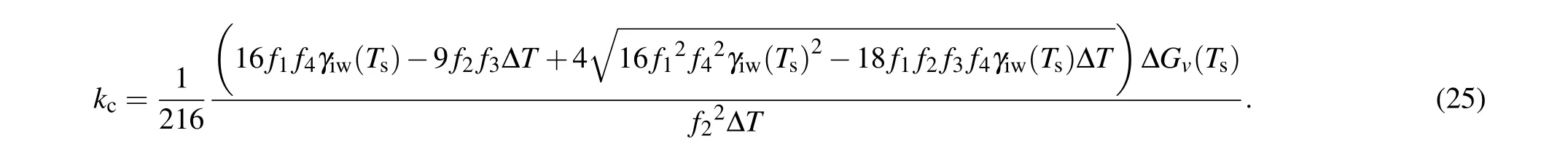
It should be noted thatkchas a definite value for the given contact angle and degree of supercooling due to the results of 16f12f42γiw(Ts)2−18f1f2f3f4γiw(Ts)∆Tin the above equation always being larger than zero exceptθ=0◦.

Figure 6 shows the effects of contact angleθon the critical temperature gradientskcrelated to the degree of supercooling ∆Tgiven by Eq. (25). It can be found that for a given contact angle,the critical temperature gradient increases parabolically with the increasing degree of supercooling. At the same degree of supercooling,the smaller the contact angle,the higher the critical temperature gradient and the increment of the critical temperature gradient will decrease as the contact angle increases.

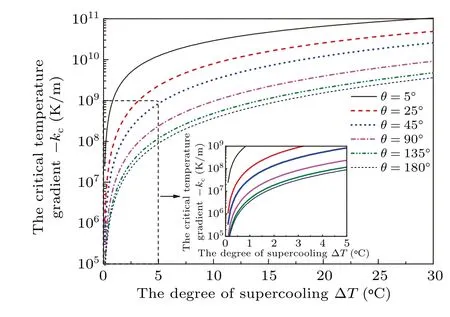
Fig.6. Relation between the critical temperature gradient and the degree of supercooling for various contact angles.

4.4. Nucleation barrier

For a given external stimulus on supercooled water, the increase and decrease of the nucleation barrier directly determine the reduction and enhancement of nucleation.Up to now,we have already known that the critical radiusrcfor nucleation in temperature gradient is dependent on the degree of supercooling ∆T, the temperature gradientkand the contact angleθ. Therefore, the nucleation barrier must also be determined by these three factors. To efficiently evaluate the effect on nucleation barrier,we define the following two factors:

1. Similar to the Fletcher factor, which reflects the reduction on the nucleation barrier for heterogeneous nucleation compared to the homogeneous nucleation because of the presence of foreign bodies,a factorfkis given as

to reflect the corresponding reduction on the nucleation barrier in the presence of temperature gradient. It is foreseeable that it is not only related to the contact angle,but also related to the temperature gradient and the degree of supercooling. It should be noted that to makefkhave an actual value, the temperature gradient supplied should be lower than the critical temperature gradient forθ=180◦illustrated in Fig.6.

2. To estimate the effect of temperature gradient on the change in the nucleation barrier,a factorCis given as

It is also related to the contact angle and the degree of supercooling. As a result,ifC ＞1 implying that the nucleation is suppressed. Conversely, ifC ＜1 implying that the nucleation is enhanced.

The changes in factorfkwith the contact angleθfor various cases are shown in Fig. 7. Compared with the Fletcher factorfwith flat geometry limit in CNT,there is a decrease infkindicating that the presence of foreign bodies will increase the heterogeneous nucleation rate relatively more with temperature gradient than that without. Furthermore, the higher temperature gradient and the lower degree of supercooling,the greater the decrease. For a given degree of supercooling, the decrease will be very significant when the temperature gradient is close to the critical temperature gradient withθ=180◦,such ask=−8×108K/m,∆T=15◦C in Fig.7,for whichkcis about−8.4×108K/m.

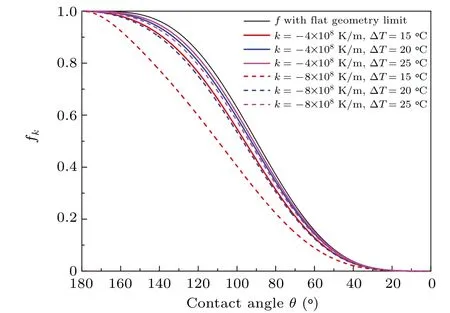
Fig.7. Factor fk as a function of contact angle θ at various degrees of supercooling in the presence of different temperature gradients and comparisons with Fletcher factor f with flat geometry limit in CNT.

Figure 8 shows the variations of factorCwith temperature gradient at various contact angles and degrees of supercooling.For all cases,Cis larger than 1 indicating the increasing Gibbs free energy which is in line with the increasing critical radius of cluster formation. For a lower degree of supercooling with same contact angle,Chas a larger value. In the meanwhile,the larger contact angle,the largerC. It is manifested that the relatively greater enhancement in nucleation barrier occurs at a lower degree of supercooling and larger contact angle. We can see thatCincreases in different forms as the temperature gradient increases. Particularly in the case of ∆T=15◦C andθ=180◦,it presents an exponentially increasing form and has no value whenkis larger than−8×108K/m. This is because the temperature gradient closing tokcfor the given ∆Tandθwill rapidly enhance the nucleation barrier, and after exceeding it,there is no maximum Gibbs free energy.For the temperature gradient lower away fromkc,such asθ=45◦,∆T=15 and 20◦C,Cincreases linearly. The similar linearity is also presented in our previous fitted results in the macroscopic experiment of temperature difference affecting the freezing temperature of supercooled water.[37]

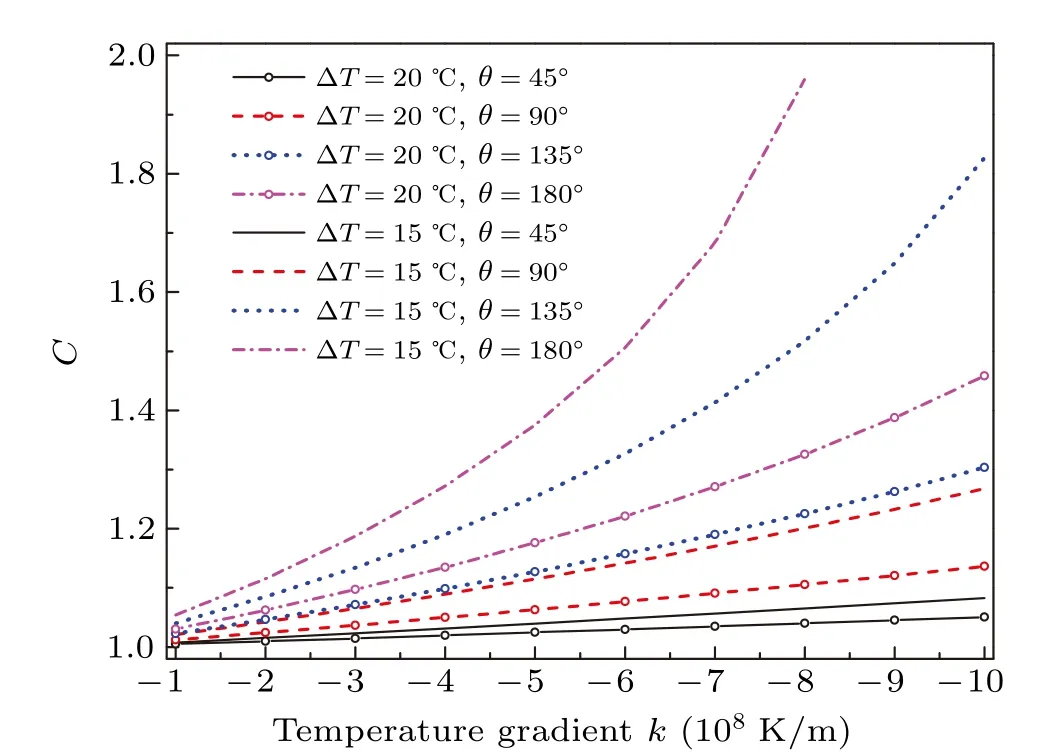
Fig.8. Factor C as a function of temperature gradient k at different degrees of supercooling with various contact angles.

4.5. Nucleation rate

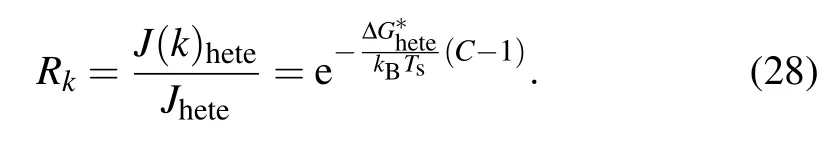
For a given case, an increased nucleation barrier will inevitably reduce the nucleation rate. The ratio of nucleation rate in temperature gradient to that in isothermal condition,denoted as Rk by us representing the level of reduction on nucleation rate due to the presence of temperature gradient,is

Figure 9 shows the nucleation rate changes with the degree of supercooling in uniform temperature for different contact angles. Figure 10 shows the relationship between the level of reduction on nucleation rateRkwith the degree of supercooling ∆Tin different temperature gradients with various contact angles. Relative to the increasing temperature gradient,the increase in contact angle from 45◦to 135◦will significantly decrease theRk. Forθ=45◦, the decreases in nucleation rate at ∆T=15◦C are less than two orders of magnitude,but it can be tens of orders of magnitude forθ=135◦. When the contact angle is large,the decreasing order of magnitude is also noticeable as the temperature gradient increases. In addition,the higher degree of supercooling,the lower the order of magnitude of reduction. Of course, if the temperature gradient applied is close to the critical temperature gradient for the high degree of supercooling, there also will be a decrease in nucleation rate with tens or hundreds of orders of magnitude.It should be mentioned that forθ=180◦, i.e., homogeneous nucleation,the nucleation rate will present heterogeneous with units of m−2·s−1since the lowest temperature area under the temperature gradient is a plane. For instance, the homogeneous rate at ∆T=30◦C will reduce about from 1016m−3·s−1to 103m−2·s−1in a temperature gradientk=−8×108K/m according to our analysis.

Fig.9. Nucleation rate as a function of the degree of supercooling with various contact angles in isothermal case.

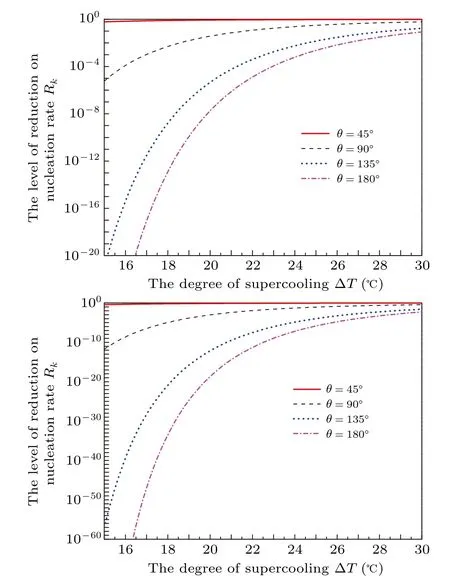
Fig.10. The level of reduction on nucleation rate Rk as a function of degree of supercooling ∆T in different temperature gradients with various contact angles. (a)k=−4×108 K/m;(b)k=−8×108 K/m.

5. Conclusions

In summary,we have carried out a thermodynamic analysis on free energy based on classical nucleation theory to investigate ice nucleation from supercooled water in a temperature gradient. How a temperature distribution in a cluster affects the behaviours of nucleation is presented. The effects of temperature gradient and contact angle on the change in free energy, critical radius, nucleation barrier and nucleation rate at various degrees of supercooling are demonstrated. The following conclusions can be drawn:

1. In the presence of a temperature gradient,during the formation of an ice embryo,the energy gain,i.e.,the volumetric free energy,will be lower than that in an isothermal case. On the contrary,the energy cost,i.e.,the surface free energy,will be higher. Therefore,a larger critical nucleus radius is required to make the volumetric free energy overcome the surface free energy. That is,a temperature gradient will increase the critical radius for nucleation.

2. Different from that the critical radius is only temperature dependent on CNT,it is also related to the temperature gradient and the contact angle between the ice embryo and substrate. For a given contact angle, the critical radius will increase with temperature gradient and becomes more obvious at a low degree of supercooling.For a given temperature gradient,the increase in the critical radius will increase as the contact angle increases and similarly becomes more significant at a low degree of supercooling.

3. When the temperature gradient is large enough,the energy gain no longer overcomes the energy cost even if the cluster grows infinitely. Thus,there is a critical temperature gradient for the given contact angle and degree of supercooling, at the higher of which the ice nucleation can be suppressed completely.In addition,the critical temperature gradient will increase as the degree of supercooling increases and the contact angle decreases.

4. The factorfkreflecting the reduction on the nucleation barrier for heterogeneous nucleation compared to the homogeneous nucleation in the temperature gradient is smaller than the Fletcher factor in CNT. The factorCrepresenting the increase in Gibbs free energy under the effect of the temperature gradient increases linearly when the temperature gradient is lower away from the critical temperature gradient, and presents a parabolic increasing form when closing to the critical temperature gradient.

5. A larger degree of supercooling is needed to initiate nucleation in temperature gradients. An appropriate temperature gradient can significantly reduce nucleation rate in tens or hundreds of orders of magnitude, particularly with a large contact angle and at low degree of supercooling.

The hypothesis of ideal linear temperature distribution in the cluster and surrounding water in the current work is inconsistent with the actual situation,which will cause an error between the analytical results and the real values,but no matter what form the actual temperature distribution is, as long as there is a temperature gradient, the nucleation barrier will increase and the corresponding nucleation rate will decrease.It can be verified from macroscopic experimental phenomena that a larger degree of supercooling can be obtained when supercooled water is cooled with a temperature difference.[34,37]In order to eliminate discrepancies caused by model simplification and assumptions, more accurate temperature distribution within the cluster and on the interface between the water and ice embryo needs to be studied in depth, and the corresponding strict experiments need to be designed with the help of the relevant numerical simulation and advanced experimental techniques[59–61]in future work. Our analysis and results will help us to understand ice nucleation under nonequilibrium conditions in fundamental researches,and to better control the stability of supercooled water by using a temperature gradient in practical applications.