在数学教学中注重训练学生的数学能力

杨顺初

初中数学课程标准，除强调学生的技能、能力、思想方法之外，还特别强调了学生的数学应用能力、数学交流能力、数学情感态度价值观与自信心，数学欣赏能力等，并鼓励学生大胆地创新。因对学生的数学能力有了新的要求，那么在对学生进行能力训练的过程中，也应有新的要求。笔者在此仅提出自己的管窥之见，以求教于大方之家。

一、训练中加强过程性训练，注重学生对知识发生过程的探索

学生只有了解知识的发生规律，并亲自体验了知识的发生过程，才能较深刻地了解知识，较牢固地掌握知识，才可能更灵活地运用知识。例如：在引导学生探索多边形的内角和时，分以下几个步骤：

（1）分别画出下列多边形由一个顶点出发的所有对角线。

（2）上述每个多边形所画的对角线将多边形分成了多少个三角形?

（3）观察多边形中所有的三角形内角和是否是多边形的内角和。

（4）填表、找规律：

学生通过自己动手探索参与知识的发生过程，不但了解了多边形的内角和与三角形内角和之间的联系和演变，而且对多边形的内角和公式也有了十分深刻的印象，并从而牢固掌握了相关知识。在积极主动参与全过程中，训练了学生的观察能力。

二、在训练中加强层次性训练，循序渐进地促进知识技能、思想方法的掌握与提高

学生思维的发展有一个循序渐进的过程。以往教师只注重学生思维的最后结果，至于如何进行思维训练的“阶梯式”过程则被忽视了。若对学生缺乏思维“阶梯”式的训练、分层次的指导，学生就不能抓住事物内在的联系进行联想、想象、创造，对创新能力的培养和提高将大打折扣。

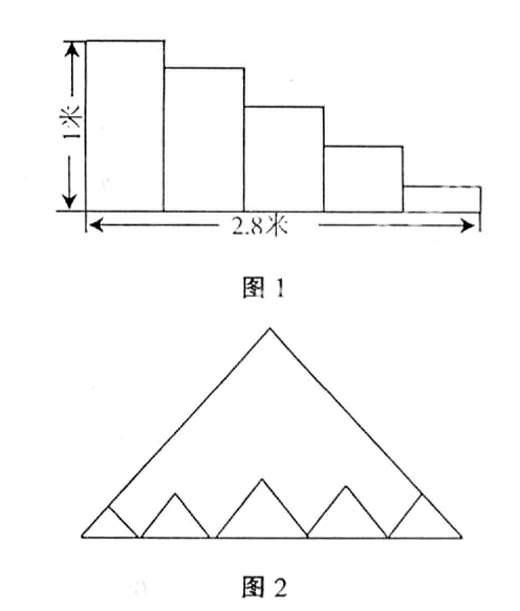
例1：图1是5级台阶的侧面示意图，如果在台阶上铺地毯，那么至少要买地毯多少米？

例2：如图2，已知等腰直角三角形，把斜边任意分成五段，分别以这五段为斜边再画出五个小等腰直角三角形，

试比较所有小三角形周长和大三角形周长的关系。

以上两道例题若放在八年级上期学完平移后给学生练习，学生利用平移做出例1后，对于例2，学生只要认真观察比较，就能找出解答的方法。这就呈现出了训练的层次性，按循序渐进的规律训练了学生的思维能力。

三、在训练中加强活动性训练，增强学生的合作交流能力

随着现代社会的迅猛发展，单个个体在社会中的作用已经显得越发渺小，更多的事务要求人们进行合作交流。在训练过程中，若能加强学习的活动性和趣味性，则能使学生乐意积极参与并与同学合作交流，能使他们克服一定的困难，寻找出解决问题的方法，从而锻炼克服困难的意志，并使他们获得一定的成功体验，这对拓展解题思路、增强自信心、培养创造性思维均十分有利。

例3：剪四个同样大小的等边三角形，你能将这四个三角形拼成一个三角形吗？四边形呢？它们各是什么图形？

通过学生动手制作，合作交流，从中发现以上图形可拼成等边三角形、正方形、平行四边形。在此过程中，不同的学生可能有不同的解决办法，无形中培养了学生思维的多样性。

四、在训练中要突出差异性，使所有学生都能得到应有的发展

任何班级的学生在能力上、思维上都有差异性，因而学生逐渐形成的自我意识水平、爱好兴趣就有差异，每个人的发展方向，乃至最终的发展水平都会不同。因此在训练中，教师应充分认识并针对个体差异开展工作，因材施教，因人而异。

例4 ：①在△ABC中，AB=AC，∠B、∠C的平分线BO、CO相交于点O，过点O作EF∥BC，交AB于E，交AC于AF，图中有几个等腰三角形？EF与BE、CF之间有怎样的数量关系？

②在第①题中，去掉AB=AC，其他条件不变，图中还有等腰三角形吗？有几个？EF与BE、CF之间又有怎样的数量关系？

③在第②题中，改CO平分∠ACB为CO平分外角∠ACD，其他条件不变，图中还有等腰三角形吗？有几个？EF与BE、CF之间有怎样的数量关系？

综上所述，要提高学生的数学素质，数学能力，教师对学生能力训练中的设计和指导是关键。只有使训练形成序列性、层次性、活动性、科学性,突出差异性,才能有效促进学生的发展和数学素质的提高。