新老教材有效整合点滴谈

邢金凤

最近，笔者听了四年级下“认识三角形”一课，本节课的教学内容呈现如下特点：三角形的特征简洁明了，易学易懂；但三角形三条边的关系探索困难重重。在学生较快地掌握三角形边、角和顶点的特征之后，老师出示了一组判断题：

下面哪些图形是三角形，为什么?

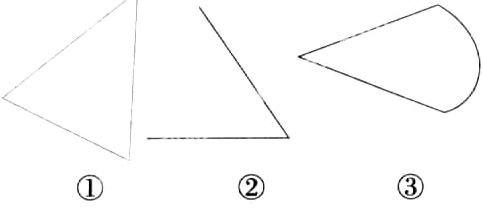
学生凭直觉很快得出：②③不是三角形，在追问②为什么不是三角形时，学生的表述恰如“茶壶里煮饺子——倒不出”，心知肚明却难以表达，有的说“那条边没有画到头”，有的说“那里有缺口”，始终无法用规范的语言清晰准确地表达出来，老师也含糊其词：这两条边两个端点没有重合，所以这个图形不是三角形……

此时，我不由得想到老人教版教材中关于“三角形认识”的一句话：“三条线段围成的图形叫做三角形”。我在想，在这个教学环节如果这位教师注意使用老教材这句话，可以使学生认识更准确，理解更深入，表述更简洁。课后，我与这位教师交流：老教材中关于三角形的概念你了解吗?（知道，我教过的。）你如何看待老教材中关于三角形的描述?（简洁、准确。）那你为什么没有使用呢?学生表达不清可以理解，你在小结时完全可以一语中的：三角形是由三条线段围成的图形，这对于后面用小棒围三角形探索三条边的规律也很重要啊。（不敢，新教材中没有这句话。）……

确实，新教材通过题材选择、结构编排等体现新的数学教学理念，以期望有效地促进师生的共同成长。然而，新教材在带来观念变化的同时，有时也让我们体验到一定的尴尬，甚至无所适从。“结识新朋友，不忘老朋友”，使用新教材，不忘老教材。我想，我们若能在新教材使用过程中结合学生实际情况，有机整合与老教材的相关内容，应该会使我们的课堂锦上添花，学生也能更好地发展。那么如何才能有效整合新老教材，提高课堂教学效率呢?下面结合本人的实践和体验，谈几点肤浅的认识。

1．从更适合学生认知规律的角度整合教材

虽然《教师教学用书》“教材说明和教学建议”中指出：“应用等式的性质解方程，较好地解决了关于方程解决的中、小学衔接问题。教材改变了在小学阶段利用四则运算的互逆关系及相关运算律解方程的传统做法，引入了等式的性质，并应用等式的性质解方程。”但是，在五下“方程”（苏教版国标教材）教学中，我们却遭遇了令人尴尬的场面。

教学例7“列方程解决问题”后，师生共同研究“练一练”：

学生有了如下的解法。

今年的体重-去年的体重=2．5（千克）

解：设去年体重为X千克

36-X=2．5

36-X-36=2．5-36

至此，学生愣住了，列的方程没有错，可解方程却遇到了困难，等式的性质难以用上。此时，只能另辟蹊径，重新寻找数量关系探求解决问题的方案。

纵观整个教材，虽然编者精心编排，教材中没有直接呈现类似的方程，然而学生的思想无法控制，在列方程解决问题时，出现此类方程难以回避。虽然从成人思维角度看，这类方程也可以运用等式的性质解：

36-X=2.5

36-X+X=2．5+X

36=2.5+X

2.5+X=36

2.5+X-2.5=36-2.5

X=33．5

但是，解答一个简单的方程，如此复杂、繁琐，很难说易于学生理解、掌握。我觉得从学生的认知规律看，这里运用老人教版教材中“四则运算的互逆关系”更简洁，也更利于学生理解和掌握：

36-X=2.5

X=36-2.5

X=33.5

所以，我认为方程教学，适度整合新老教材中的不同方法，符合学生认知规律，有利于学生发展。

2.从更有利于学生数学学习的角度整合教材

曾经看过一篇关于“短除法教还是不教”的文章，新教材中去掉了“短除法”这一内容，虽然其中有一定的道理，但从学生发展角度考虑，把老教材中“短除法”的知识适当地介绍给学生，至少有三点必要：①短除法是古代算学瑰宝之一，学生有了解并继承的必要；②有利于学习上有余力的学生快捷地找到公分母，尤其是几个分数的公分母或数值稍复杂的公分母；③可以针对不同层次的学生，让他们有更宽泛的学习选择空间，方法更灵活，从而有力地体现出新课程“不同的学生，学习不同的数学，获得不同的发展”的理念。

总之，教材整合要合时、合理、合情，取长补短，有效整合，提高效率。应该说新老教材各有特色，既各有优点，又各具不足。这就给我们数学教师提出了较高的要求，既要吃透新教材，又要熟悉老教材，尤其是老教材的长处。

最后，我想说，教材是由教育专家们精心编写而成的，是前人丰富经验的综合。但由于教材受人员、地区、环境等条件的影响，它不是“万能书”，也有不断完善、不断建设的必要。教师执教中应该借助教材，整合内容，灵活运用，让教材焕发新的活力，以便较快提高学生学习效率。