新型舰炮平衡机的分析与计算

康 郦 胡 月 朱承邦

大连船舶重工集团有限公司军事代表室，辽宁大连116005

新型舰炮平衡机的分析与计算

康 郦 胡 月 朱承邦

大连船舶重工集团有限公司军事代表室，辽宁大连116005

发条簧式平衡机是一种性能先进的动态平衡机，满足了现代自动火炮高发射率、高精度和轻型化的要求。以100 mm舰炮为例，对发条簧式平衡机进行了定量分析，通过分析得出该型平衡机在动态和静态时对火炮的影响规律。探讨平衡机设计思想和调试方法。

舰炮；平衡机；定量分析

1 引言

目前世界各国装备的自动火炮中，有些采用了配重平衡，有些采用了拉压弹簧式或液体气压式平衡机，这种平衡方式只能粗略地满足火炮的俯仰平衡，不能满足火炮在后座过程中的平衡。本文介绍一种新型的动态平衡机，即大扭矩发条簧式平衡机。意大利OTO 76 mm舰炮和法国紧凑型单100 mm舰炮均采用了该类平衡机［1］。法国紧凑型单100 mm炮塔采用了包括新型发条簧式平衡机在内的多项设计改进，在射速提高50%的情况下炮塔质量反而下降了35%［2］。与我们常用的传统火炮平衡机相比，该平衡机在功能上和设计思想上均有许多独到之处。

2 工作原理与结构特点

该平衡机结构比较简单，发条簧（以下简称弹簧）安装在炮架左右两侧，耳轴上后方（图1）。弹簧的外端头并联地固定在炮架上，内端头并联地固定在左右心轴上，心轴外端与平衡机滑轮用花键连接在一起。通过钢丝绳BN把滑轮与火炮后座部分柔性地连接起来。当火炮做俯仰运动和后座运动时，通过钢丝绳BN带动左右滑轮转动，从而使平衡机弹簧转角发生变化。平衡机所产生的扭力矩通过滑轮和钢丝绳作用在火炮的俯仰部分上，产生一个逆时针方向的力矩，以抵消重力矩和后座部分质心变化时对火炮的影响，使火炮始终保持平衡状态。

图1 发条簧式平衡机结构简图

3 数学模型

为了更深入地了解发条簧式平衡机的性能特点，有必要建立发条簧式平衡机的数学模型，推导出方便适用的数学公式。为动态平衡机的调试及分析火炮的受力状态提供一些必要的参考。

3.1 平衡机力与力矩的分析计算

为了分析问题方便，建立图2所示坐标系和模型图。OW为水平轴，OQ为铅垂轴。另建立XOY动坐标系，OX为炮膛中心线方向，OY垂直于OX向上。在分析和计算过程中各种参考量符号说明如下。

图2 平衡机工作原理图

图2中，B为平衡机钢丝绳与后座部分的挂接点；b为DB长度；ф为火炮射角；α1为∠BDO；α2为∠NDB；O为火炮耳轴中心点；D为平衡机滑轮中心点；β为平衡机弹簧工作时转角；N为钢丝绳与平衡机滑轮切点；L为切点N到B点距离；a为耳轴中心线到平衡机滑轮中心线的距离；X为火炮后座长；S为静态时耳轴中心线到B点距离；R为平衡机滑轮半径。

3.1.1 平衡机弹簧转角β同火炮射角ф，后座长X之间的关系

在粗调平衡机时，根据火炮重力矩的大小以及变化规律来确定平衡机的初始工作角度。对于确定的火炮，当射角ф＝ф0、X＝0时，把平衡机初始工作角度定为β0，这时火炮接近平衡状态。当火炮运动时，随着射角和后座长的变化，钢丝绳与平衡机的切点N以及BN段钢丝绳的长度在不断变化，从而带动平衡机弹簧开始工作。通过分析BN段钢丝绳的伸长量以及切点N的位置改变就可得出平衡机弹簧在任意状态下相对ф＝ф0、X＝0时的转角，从而确定任意时刻平衡机的工作角度。

为了分析问题方便，先明确以下各量的含义，见图2。

∠DOW由D点坐标确定，DO＝a，DN＝R均为已知常量。

令θ＝∠DOB＝∠DOW－ф

OB＝s－x，s为火炮没后座时OB线段长。在△DOB中，

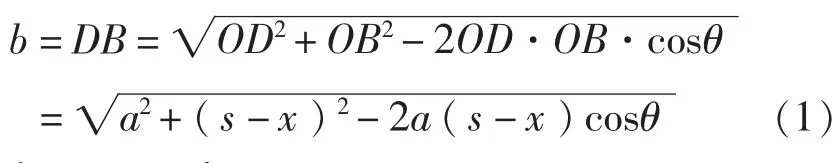
在△NDB中，

在△ODB中，在任意状态下钢丝绳与炮膛中心线夹角：

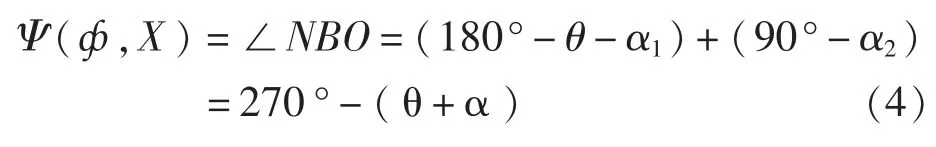
把ф＝ф0、X＝0代入式1）～式4）中，就可以计算出b0、L0、α0、Ψ0的值。

求出以上这些初始条件可以求出火炮在射角为ф，后座长为X时平衡机的工作角度。如图3所示。假设N0为ф＝ф0、X＝0时钢丝绳与滑轮的切点。在切点由N0变化到N1的过程中，钢丝绳相对定坐标系中N0点的伸长量（弧长）为：

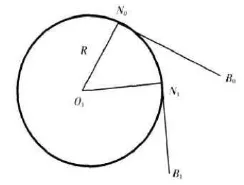
图3 绳子伸长量与平衡机弹簧转角关系图

由于钢丝绳伸长的那一部分原来缠绕在滑轮上，所以N1时刻平衡机弹簧的工作角度为：

式 （5）就为平衡机在任意时刻的工作角度（°）。

3.1.2 平衡机对火炮的力及力矩

平衡机弹簧在转角为β（ф，X）时，n片弹簧产生的扭力矩Mt，钢丝绳上的涨力F，对火炮的力矩M均是火炮射角ф和火炮后座长X的函数。

在平衡机弹簧转角为β（ф，X）时，n片发条簧所产生的扭力矩为［3］：

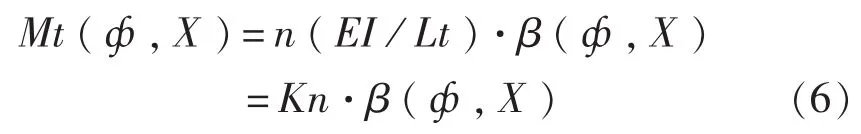
式中，E为弹簧材料的弹性模量，对合金弹簧钢E＝2.15×106kg／mm2；I为材料的截面惯性矩，I＝b a3／12；a为弹簧厚度；b为弹簧宽度；Lt为弹簧的有效展开长度；Kn为n片弹簧的刚度值，Kn＝n·（EI）／Lt；

由于平衡机滑轮半径为R，故钢丝绳上的涨力为：

平衡机产生的沿后座方向和垂直后座方向的分力分别为：

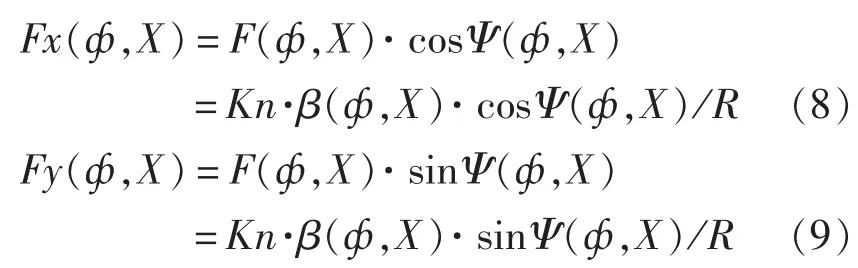
任意状态下平衡机对火炮的力矩：

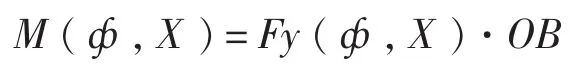
将式（4）、式（5）代入后得：

α、L、θ的函数前面已推出。

式（10）就是平衡机对火炮力矩变化规律的定量关系式。

通过编程计算得出了β（ф，X）、M（ф，X）、F（ф，X）、Fx（ф，X）、Fy（ф，X）等参量在全射角和全后座长上的变化数表，只要任意给出一个射角ф和后座长X，就可以方便地查出以上各值。以单100 mm舰炮为例，M（ф，X）动态时变化趋势如图4所示；静态时变化趋势如图5所示，Fx（ф，X）、Fy（ф，X）等具体变化情况见表1和表2。

3.2 火炮重力矩的分析与计算

3.2.1 重力矩变化规律关系式

火炮重力矩包括两部分：

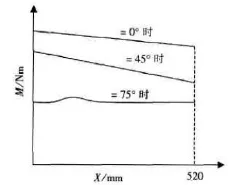
图4 动态时M（φχ）变化趋势曲线

图5 静态时M（φχ）变化趋势曲线

表1 β、M、Mg、ΔM′、Fx、Gx静态时变化规律表

表2 β、M、Mg、ΔM′、Fx、Gx动态时变化规律表

1）后座部分重力矩。这一部分重力矩将随射角ф和后座长X的变化而变化。令后座部分重量为G1，重心为Z1（x1，y1）。

2）不后座部分重力矩。它只随射角ф的变化而变化。令这一部分的重量为G2，重心为Z2（x2，y2）。

后座部分重力矩为：

非后座部分重力矩为：

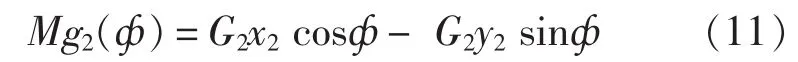
整个俯仰部分的重力矩为：

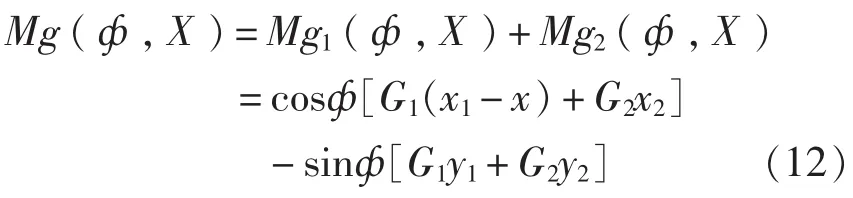
对式中各量做如下规定：x1、x2在耳轴前侧（炮口方向）为正，y1、y2在炮膛中心线上侧为正，反之均为负。

3.2.2 动态时重力矩的变化规律

下面进一步研究动态时重力矩变化规律。在某一射角射击时，cosф、sinф均为常数，只有后座长x一个变量，这时式（12）可以写为：

对于确定的火炮，上式中第一项为一常数C1；第二项中G1cosф也为一常数K1，于是式（12）可以写成：

从式（13）可以看出，随着火炮后座，其重力矩按线性规律减小。

3.2.3 静态时重力矩变化规律

这时x＝0，只有射角ф一个变量，于是式（12）可以写为：

式（14）中（G1x1＋G2x2）和（G1y1＋G2y2）对于每门火炮都为确定的常数。且y1远小于x1，y2远小于x2。在要求不十分严格的情况下可以忽略式（14）中的第二项，并令G1x1＋G2x2＝Kф，则式（14）可以写为：

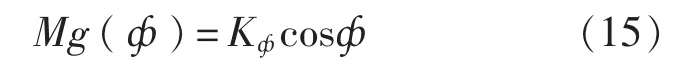
从式（15）可以看出，静态时火炮重力矩基本按余弦函数规律变化。平衡机与重力沿后座方向的分力为：

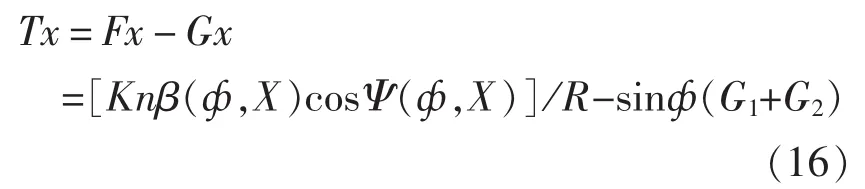
重力矩的详细变化情况见表1和表2。

3.3 不平衡力矩的分析与计算

由前面式（10）及式（12）可得火炮不平衡力矩函数式为：

式（17）就是火炮不平衡力矩变化规律的定量表达式。力矩顺时针方向为正，Mf是火炮摇架上下护板等处总的摩擦力矩。火炮仰上时Mf为正，俯下时为负。从式（17）可以看出，火炮不平衡力矩波动主要受Mg（ф，X）和M（ф，X）的影响。对于确定的火炮，在后座部分、俯仰部分的重量与重心已知的情况下，通过编程计算就可得出ΔM的变化曲线。在调试时可以利用改变G2的办法进行优化计算，从而使火炮达到最佳平衡状态。通过计算得出了单100 mm舰炮不平衡力矩在动态和静态时的变化趋势（见表1和表2）。

4 动态平衡机的调试方法

4.1 不平衡力矩电流曲线分析

精调平衡机时，用测量高低机电枢电流的方法来检验不平衡力矩的大小及波动情况。实测的单100 mm舰炮不平衡力矩电流变化曲线如图6所示，令ΔM′＝［Mg（ф，X）－M（ф，X）］＜0，即重力矩此时小于平衡机力矩。由于摩擦力矩Mf始终和火炮运动方向相反，则火炮仰上及俯下时的电流值分别为：

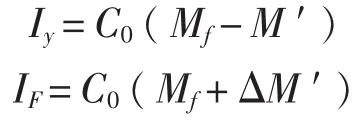
由所测的不平衡力矩电流曲线分析可知，Mf＞ΔM。解该方程组得：

图6中曲线②为摩擦力矩所对应的电枢电流曲线；曲线①为火炮仰上时对应的电枢电流曲线；曲线③为火炮俯下时所对应的电枢电流曲线。从理论上讲曲线①和曲线③关于曲线②对称。曲线②决定着电流值的大小；曲线①和曲线③反映了不平衡力矩的波动情况。在H点ΔM′（ф）＝0，即这一点Mg（ф）＝M（ф）称为平衡点。在这一射角上只有摩擦力矩Mf。

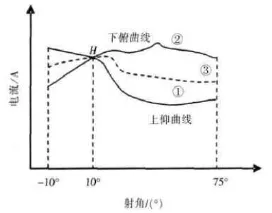
图6 不平衡力矩电流曲线

4.2 动态平衡机的调试方法

在精调平衡机时怎样判断 ΔM′（ф）＝Mg（ф）－M（ф）的方向以及怎样配重？

对于同一射角ф在平衡点H右侧，如果电枢电流Iy＜IF，则说明M′（ф）＜0，即Mg（ф）＜M（ф），此时应减少配重。见图2，如配重处到耳轴中心线距离为Lg，应减少配重为：

ΔM′（ф）为电机轴上反映出来的不平衡力矩波动值，由电枢电流标定值结合式（18）、式（19）就可以求出ΔM′（ф）的大小。Kg为电机轴到高低机齿弧的传动比。如配重减小量大于Gp会使Mg（ф）＞M（ф），这时再减少配重反而会使不平衡电流增大。如Iy＞IF，则说明Mg（ф）＞M（ф），这时应增加配重。由于平衡机粗调后，火炮已基本处于平衡状态，所以精调平衡机时加减配重只是微量的。

也可根据ΔM′（ф）的大小和方向通过改变平衡机弹簧初始角的办法进行粗调，这里不再赘述。值得说明的是，ΔM′（ф）永远不会是一条直线，因为随着射角的变化Mg（ф）与M（ф）遵循不同的规律。但ΔM′（ф）有一个最佳值，该最佳值只有利用本文方法通过计算后，并进行充分的调试才能得到。某型火炮的最佳平衡状态曲线见图7。

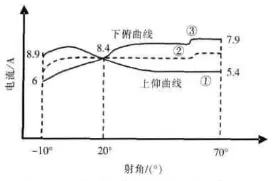
图7 应用本文方法调试出的最佳平衡曲线

5 结论

通过对单100 mm舰炮平衡机的定量研究可知，发条簧式平衡机具有以下特点：

1）俯仰平衡

以单100 mm舰炮为例，在射角从－15°～0°逐渐增大的过程中，重力矩和平衡机力矩都呈逐渐增大的趋势；在射角从0°～80°逐渐增大的过程中，重力矩及平衡机力矩都呈逐渐减小的趋势。火炮的不平衡力矩随射角变化波动较小，实现了全射角平衡，提高了火炮的瞄准精度。

2）后座平衡

单100 mm舰炮俯仰部分重心在耳轴前侧，火炮后座过程中重力对耳轴的力矩逐渐减小，随着火炮后座，平衡机对火炮的力矩也相应减小。射击过程中不平衡力矩波动较小，而且可以保证火炮后座过程中不平衡力矩不改变方向，保持火炮后座过程中的平衡。解决了传统火炮平衡机后座复进不平衡问题，从而大大提高了火炮的跟踪精度和连发射击的稳定性，实现了全后座长的平衡。

3）后座复进运动稳定

由前面分析可知，低射角时，重力分力较小；而平衡机沿后座方向的分力Fx较大，帮助火炮后座；中射角时（30°＜ф＜60°）重力分力Gx及平衡机沿后座方向的分力Fx处于中间值，Fx在后座初期帮助火炮后座，后座到一定长度Fx改变方向，开始阻碍火炮后座；高射角时Fx和火炮后座运动方向相反，始终阻碍火炮后座。计算表明，火炮后座过程中沿后座方向的合力波动较小，火炮最大后座长随射角的变化波动较小，只有2～3 mm。火炮发射率基本上不受射角变化的影响。保证和供弹速度匹配，有利于自动化控制。

此外，发条簧式平衡机还具有结构简单，工作可靠，弹簧寿命长，易于实现等优点。该平衡机在火炮上应用后可以减小火炮后部尺寸，减小配重，降低火线高，有利于提高火炮的射击精度和舰炮的轻型化。在火炮设计中具有很高的借鉴和推广价值。

［1］康郦，苗海.记法国单管100毫米舰炮［J］.现代舰船，2001（7）：29－30.

［2］杨宇刚.国外舰炮技术与发展［M］.中国船舶重工集团公司七一三研究所，2007.

［3］张会英，罗圣国，郭荣生，等.弹簧［M］.北京：机械工业出版社出版，1992.

Quantitative Analysis and Calculation of Naval Gun's Spring Equilibrator

Kang LiHu Yue Zhu Cheng－bang
The Naval Representative Office，Dalian Shipbuilding Heavy Industry Co.，Dalian 116005，China

As an advanced dynamic equilibrator，spring equilibrator can meet modern automatic gun＇s requirements for high firing rate，high accuracy and lightweight.This paper makes a quantitative analysis of 100 mm caliber naval gun＇s spring equilibrator and the effects of the equilibrator in its dynamic and static state.

naval gun；equilibrator；quantitative analysis

TJ391

A

1673－3185（2009）02－73－05

2008-06-02

康 郦（1967－），男，高级工程师。研究方向：海军兵器