考虑流体静压时充液圆柱壳的输入能量流特性

刘志忠 李天匀 张俊杰

华中科技大学船舶与海洋工程学院，湖北武汉430074

考虑流体静压时充液圆柱壳的输入能量流特性

刘志忠 李天匀 张俊杰

华中科技大学船舶与海洋工程学院，湖北武汉430074

研究了内部流体静压力对充液圆柱壳的受迫振动能量流的影响。静压力作为预应力计入壳体振动方程当中，壳体和流体分别采用Flügge方程和Helmholtz波动方程。分析了耦合系统在周向线分布余弦载荷下的动态响应，用傅立叶变换和反变换实现空间域与波数域之间的相互转换，采用留数定理求取系统的响应并得到耦合系统的输入能量流。结果表明，周向模态数n＝0时，静压力对耦合系统的输入能量流影响很小；n较大时，在中低频下静压力使输入能量流曲线沿频率轴右移，由于输入能量流的峰值点处的频率对应于频散曲线中各支传播波的截止频率，对应传播波的截止频率升高，高频时则基本无影响。随着静压力以及周向模态数的增大，输入能量流受到的影响程度也增大。

充液圆柱壳；输入能量流；静压力；留数定理

1 引言

高压输液、输气管道在船舶、石油、化工等工业领域有着重要的应用，其振动问题已有大量的研究。振动能量流方法是研究圆柱壳结构振动问题的有利工具。Fuller等［1］利用流固耦合理论，建立了充液圆柱壳的自由振动方程，讨论了在低阶周向模态下振动波的传播特性，并得到了其自由振动的能量在流体和壳体内的分布。徐慕冰等［2］采用留数定理得到充液圆柱壳在周向余弦线分布载荷作用下的能量流输入，并讨论了沿着轴向传播时的壳体内力和流体所携带的能量流随频率的变化规律。XU等［3］采用加阻尼数值积分方法得到充液圆柱壳的输入能量流。这些文献并未考虑管内流体的静压作用。汪勇和兰波［4］采用壳体几何非线性理论，通过在系统自振方程中引入附加刚度矩阵，分析了液体静水压力对圆柱形储液容器自振频率的影响。谢官模［5］用Harmilton原理和Green函数方法研究了环肋圆柱壳在环频率以下频段的声辐射，讨论了静水压力对壳体声辐射特性的影响。Keltie［6］将静压力作为预应力项计入壳体自由振动方程，分析了静水压力对点激励下流场中圆柱壳的结构响应及声辐射的影响，并与空气中的情况做了对比。

本文采用留数定理求取无限积分来得到系统的输入能量流，研究了考虑静压作用下充液壳和未充液壳中的能量流输入特性，并与不考虑静压时的情形做对比，考察了静压对系统能量流输入的影响。

2 充液圆柱壳在周向线力作用下的强迫振动

假设无限长充液圆柱壳在截面x＝0处作用周向余弦线分布载荷为：

式中，F0表示在x＝0处的周向余弦分布力的幅值，N。

考虑内部充有流体的圆柱壳，假设圆柱壳为无限长薄壳，流体为理想流体。以x，θ和r分别表示壳体的轴向、周向和径向，u，v和w表示壳体中面轴向、周向和径向位移。圆柱壳的坐标系与周向模态数n如图1所示。

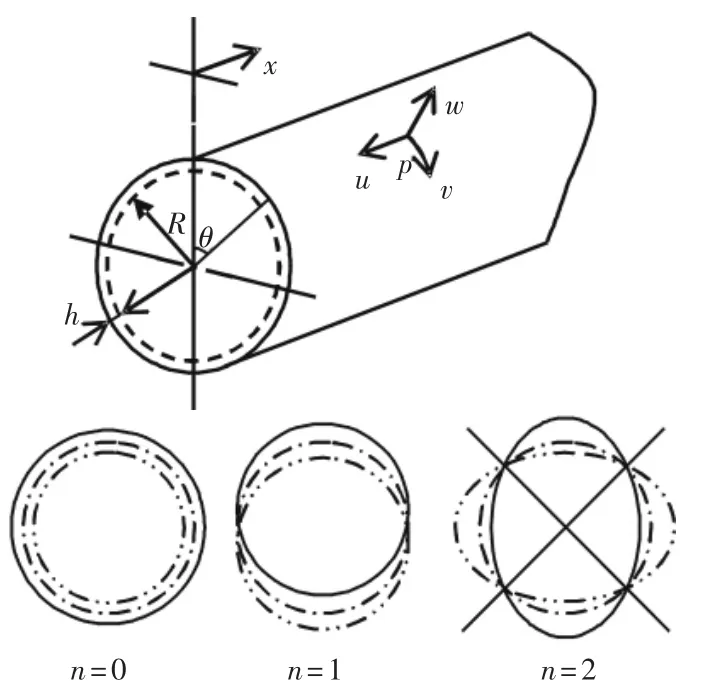
图1 圆柱壳坐标系和周向模态数n

静压力引起的初始应力包括周向应力和轴向应力。计及静压力，无限长薄圆柱壳自由振动的方程采用Flügge方程［7］。

方程的解采用如下形式：

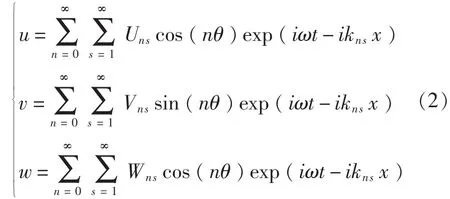
满足柱坐标系下的Helmholtz波动方程的流体声压场解为：

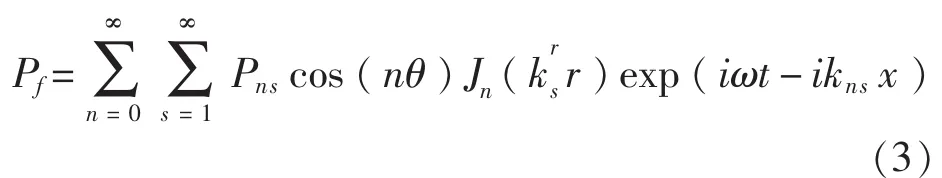
式中，kns为轴向波数，krs为径向波数，Jn（）为第n阶Bessel函数。

在流体与壳体的接触面上，流体径向位移必须等于壳体的径向位移，即

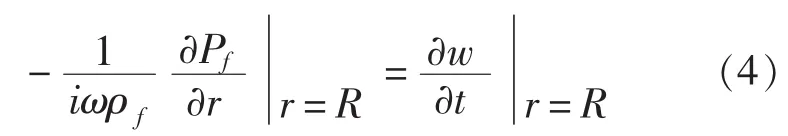
将式（2）、式（3）中的壳体位移、流体载荷以及外作用力做傅立叶变换并代入到式（1）、式（4）中，便得到此耦合系统的受迫振动方程，用矩阵形式表示为：

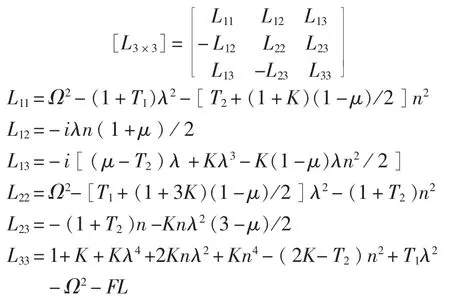
当内部没有充液而是充满轻流体时，可以不考虑流体影响，此时FL＝0。

式（5）两边同时左乘矩阵L3×3的逆矩阵I3×3，因而波数域中的位移为：

对式（6）做傅立叶逆变换，得到空间域的位移，

由式（7）可知I13，I23和I33的奇点即频散方程det L＝0的根，那么运用留数定理有

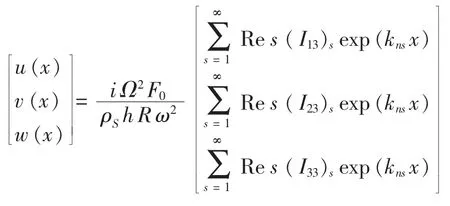
耦合系统在外线分布载荷作用点x＝0处的径向位移为：

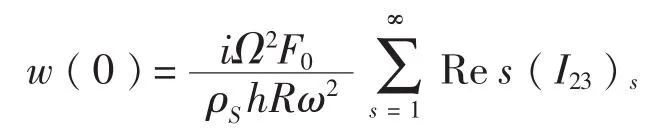
单位长度外线力输入到系统的能量流为：

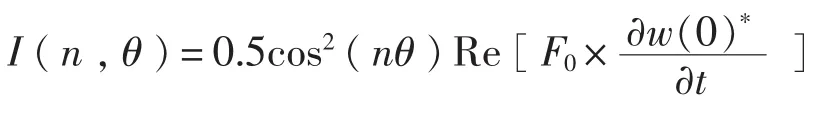
其中，*表示复共轭。由能量流的定义，外力输入到系统的能量流为：

将输入能量流无量纲化为：

3 计算结果与讨论

壳体参数：材料为钢，弹性模量E＝1.92×1011N／m2，泊松比μ＝0.3，密度ρS＝7 850 kg／m3，壳厚比h／R＝0.02。流体参数为：自由波传播速度Cf＝1 500 m／s，液体密度ρf＝1 000 kg／m3。

本文仅用传播波对应的留数计算积分值，这样只需求取频散方程的实根，采用二分法可较容易地求解。文献［2］中表明，仅用传播波对应的留数计算积分与考虑共轭驻波和近场衰减波的结果完全一致。

图2表示周向波数n＝0，1，2，5时在初始内压作用下充液圆柱壳的输入能量流。图中3组曲线分别表示在静压力P＝0 MPa、1 MPa和10 MPa下充液圆柱壳的输入能量流随频率变化曲线，P＝0 MPa表示不考虑静压力影响。由图2中的结果可得到以下结论。

1）对任何周向模态，P＝1 MPa时的输入能量流曲线基本与P＝0 MPa时的输入能量流曲线完全重合，这时考虑流体静压力对系统输入能量流没有影响。

2）当静压力P＝10 MPa时，对任何周向模态，静压力使Ω＝0.7处的能量流峰值降低，其原因是静压力使壳体的刚度增大，输入能量流减小。而在环频率以上的中高频范围内静压力对输入能量流基本无影响，这是由于第一支传播波的能量流输入占整个能量流输入的绝大部分；当周向模态数n＞1时，可以看到曲线在环频率（Ω＝1）以下向右平移，并且无论是否考虑静压力的影响，在低频外载荷没有输入能量流，其原因是低频时耦合系统中没有传播波。

3）当n＞1时，对照图2中P＝10 MPa和P＝0 MPa的能量流曲线，发现在开始有能量流输入后会有一个尖峰，并且P＝10 MPa的能量流曲线的峰值明显比P＝0 MPa的峰值大。

4）对照图2（d）中输入能量流曲线和图3中的频散曲线，可以发现相同流体静压力下输入能量流的峰值点相应的频率对应于频散曲线中传播波的起始频率。

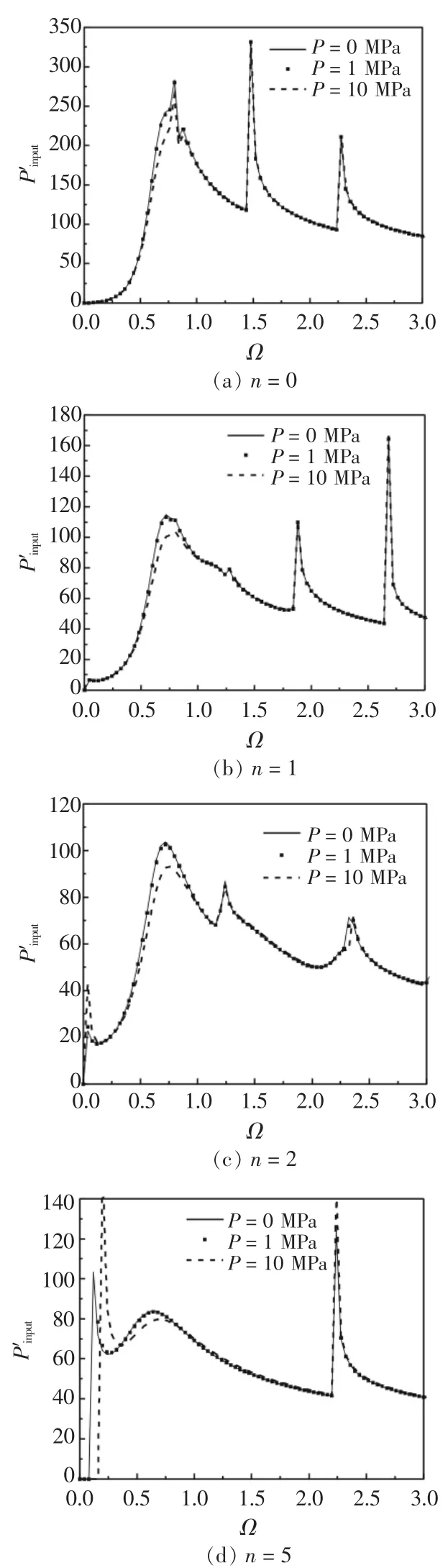
图2 考虑静压力下充液圆柱壳的输入能量流

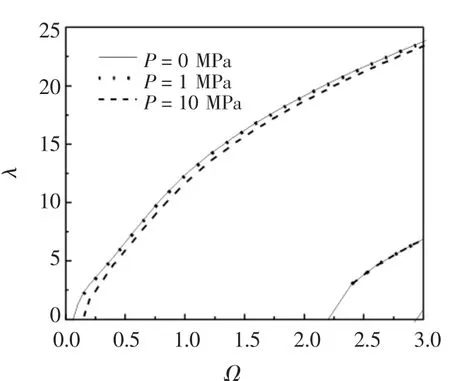
图3 充液圆柱壳中频散曲线（n＝5）

4 结论

对壳体中振动能量流的输入进行了研究，考虑了内部初始静压力的影响。通过考虑静压力的输入能量流曲线与不考虑静压力的输入能量流曲线对比，得出以下结论。

1）静压力对充液圆柱壳与未充液圆柱壳中的输入能量流特性的影响一致。

2）对任何周向模态，较小的静压力对壳体中能量流的输入基本没有影响。

3）静压力较大时，在低阶周向模态时对输入能量流基本没有影响；在高阶周向模态时，静压力使Ω＝0.7处的能量流峰值降低，并且使输入能量流的起始频率升高。

［1］FULLER C R，FAHY F J.Characteristics of wave propagation and energy distributions in cylindrical elastic shells filled with fluid［J］.Journal of Sound and Vibration，1982，81（4）：501－518.

［2］徐慕冰，张小铭，张维衡.充液圆柱壳受迫振动的能量流输入及传播［J］.声学学报，1999，24（4）：391－399.

［3］XU M B，ZHANG W H.Vibrational power flow input and transmission in a circular cylindrical shell filled with fluid［J］.Journal of Sound and Vibration，2000，234（3）：387－403.

［4］汪勇，兰波.液体静水压力对圆柱形储液容器自振频率的影响［J］.重庆交通学院学报，1997，16（2）：75－79.

［5］谢官模.静水压力对环肋圆柱壳声辐射的影响［J］.武汉工业大学学报，1995，17（1）：77－79.

［6］KELTIE R F.The effect of hydrostatic pressure fields on the structural and acoustic response of cylindrical shells［J］.Journal of the Acoustical Society of America，1986，79（3）：595－603.

［7］FlüGGEE W.Stresses in Shells［M］.Second Edition.New York：Springer－Verlag，1973.

Input Vibration Power Flow in Fluid-filled Cylindrical Shells Considering Hydrostatic Pressure

Liu Zhi－zhong Li Tian－yun Zhang Jun－jie
College of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

The effects of internal hydrostatic pressure on input vibration power flow in cylindrical shells filled with fluid were investigated.The hydrostatic pressure was modeled using static pre－stress terms in the shell equations of motion.The structural and fluid equations of motion were taken from Flügge thin shell theory and Helmholtz wave equation respectively.By using the Fourier transform and its inverse transform and applying residues theorem，the input power flow into the coupled system under a line circumferential cosine harmonic driving force was studied.The results showed that the hydrostatic pressure had practically no effect on input power flow for circumferential mode order n＝0.For high circumferential modes，the input power flow curves translated to right along frequency axis when considering hydrostatic pressure at mid and low frequencies.Since the frequencies of the peaks in the input power curve corresponded to the cut－on frequencies of the propagating waves in the dispersion curves，the cut－on frequencies of the corresponding propagating waves increased.For higher pressure and larger circumferential mode order，the effects input power flow was more significant.

fluid－filled cylindrical shell；input power flow；hydrostatic pressure；residues theorem

O328

A

1673－3185（2009）02－20－04

2008-11-03

总装备部预研基金

刘志忠（1980－），男，博士研究生。研究方向：结构振动与噪声控制。E-mail：hichrisliu＠163.com

李天匀（1969－），男，教授，博士生导师。研究方向：船舶与海洋工程结构力学