临时开口船体结构强度数值分析

周 波 刘玉君 段 宏 杨 龙 滕树生

1大连理工大学船舶工程学院，辽宁大连116024 2中国舰船研究设计中心，湖北 武汉430064

临时开口船体结构强度数值分析

周 波1刘玉君1段 宏2杨 龙2滕树生2

1大连理工大学船舶工程学院，辽宁大连116024 2中国舰船研究设计中心，湖北 武汉430064

为了分析临时开口船体的结构强度，采用有限元方法建立典型舱段的数值模型，结合相关强度校核规范进行计算，结果表明开口的船体结构的抗弯、抗扭方面的安全性必须引起重视。通过分析得到开口参数对开口的结构强度的影响规律，对实际船体结构的临时开口具有重要的工程参考价值。

船体结构；强度分析；数值模拟；临时开口；弯曲和扭转；加强方案

1 引言

旧船改造时，为方便设备或工作人员出入舱室，经常需要进行甲板、舱壁的临时开口。有的开口达到几米宽，十几米长，并且这样的开口从主甲板一直贯穿到内底。这样大规模的修改，严重影响了结构的连续性，降低结构安全性。实际工程中有的船舶在甲地切割开口取出部分设备，再到乙地进行改造。此时，船体结构开口往往不能立刻进行封闭焊接，船舶结构型式类似于大开口船舶，但临时开口结构强度要远小于大开口船舶。有的改造船舶不能立即完工，船厂为提高经济效益而将船台或船坞用于新船的建造，而改造船舶需短期或长期在海上停靠。由于改造船舶的重量分布出现明显变化，而大量结构开口的存在带来了安全隐患。国内外已经出现多例卸货引起船舶重量分布不均，并最终导致船舶折断的灾难。

对集装箱船、大开口散货船、大开口多用途船等甲板具有大开口的船舶来说，船体的扭转刚度相对较低，特别是在波浪载荷作用下，可发生显著的扭转，从而引起舱口变形，或在船体中产生翘曲应力。大开口船舶的扭转强度可上升到与总纵强度同等的地位，因此有必要对船体进行扭转分析或弯扭耦合分析。目前海洋运输中的 “大开口船舶”主要是按照船级社规范的相应规定，来评价大开口船舶船体总强度［1－6］。

另外，在船体结构上设置大型的矩形开口，会对船舶的局部强度产生严重的影响。由于断面的削弱及几何形状的突变，不仅使结构强度有所削弱，在角隅区域产生很大的应力集中，容易产生疲劳裂缝，而应力集中的裂纹，可蔓延到甲板及其舷侧，严重的可以导致整艘船舶折断，对船体结构造成危害。大多数船舶海损事故就是因为船上开口角隅处的应力集中引起的［7］。

综上所述，船体结构临时开口强度分析十分必要，具有重要的工程参考价值。从国内外相关文献来看，研究的主要对象还是集装箱船等具有大开口的船舶。文中以典型舱段为研究对象，建立有限元模型，对结构开口强度进行计算，并分析开口参数对开口的结构强度的影响规律。

2 开口的结构强度分析

2.1 有限元模型

文中采用大型有限元程序ANSYS进行分析［8］。图1为未开口船体舱段模型和切割开口后的有限元模型，整个结构包括3层甲板，中间为一完整舱室，前后各半个舱室，开口尺寸为2.6 m×4.65 m，倒角半径为0.1 m。

图1 舱段模型

2.2 结构外载荷计算

1）静载荷分量

船舶在波浪上航行或靠港时，作用在船体结构上的外力是相当复杂的。实践表明，重力与浮力是引起船体梁总纵弯曲的主要外力。全船总的重力和浮力大小相等，方向相反，并且作用在同一条铅垂线上，即全船处于静力平衡状态。对沿船长的任一区段来说，它们是不平衡的。分析船体结构外载采用许用船体梁的静水弯矩，如图2所示。

2）波浪弯矩

依据《中国船级社钢质海船入级规范（2006）》［9］，船体梁各横剖面的中拱波浪弯矩和中垂波浪弯矩应按下列公式计算：

式中，M为弯矩分布系数；L为船长，m；B为船宽，m；Cb为方形系数，但计算取值不应小于0.60；C为系数，其中，当 90≤L≤300 m时，C＝10.75－［（300－L）／100］3／2。

3）扭矩

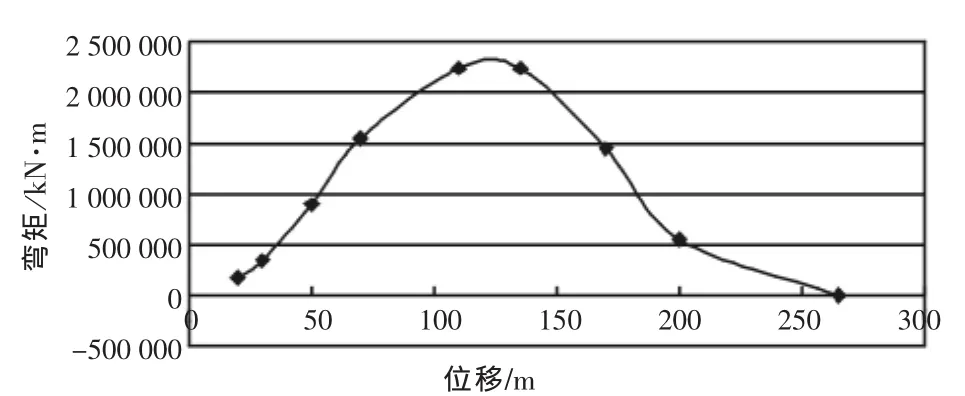
图2 静水弯矩

由于船舶结构进行了大开口，结构型式接近大开口船舶，对其扭转强度进行分析。船体受到的波浪扭矩公式，具体计算公式来自《中国船级社钢质海船入级规范（2006）》。沿船长任一剖面处的水动力扭矩MT（x）应按下式计算，单位为kN·m：

式中，e为自然对数底；L为船长，m；B为船宽，m；D为型深，m；CT＝13.2－43.4CW＋78.9C，其中CW为水线面系数，不必大于0.165＋0.95Cb；ε为从船基线以下的剪切中心至船基线的距离，m； x为从任一剖面至艉垂线的距离，m；Cb为方形系数，m。

2.3 边界条件和加载

文中以仍在营运中的临时开口船舶为例进行分析。为模拟实际船舶的受力状态，在强度计算时，在所建立的舱段模型两端根据弯曲和扭转状态加载载荷。

2.4 计算结果

经过计算，分别得到舱段结构在弯矩和扭矩作用下的结果，如图3所示。

图3 弯矩和扭矩作用下的有限元计算结果云图

从计算结果可知，结构开口后位移和应力极值显著增加。在弯矩和扭矩作用下，位移极值分别增加了16.6%和34.1%；相当应力极值分别增加了390.4%和613.9%（见表1）。从开口区相当应力云图可知，相当应力较大区域集中在开口区，其中开口倒角处最大。

综上所述，开口后船体结构的抗弯、扭能力显著降低，结果表明开口船体结构的抗弯、扭方面的安全性必须引起重视。

表1 弯曲和扭转状态下的应力极值和位移极值

3 开口参数影响规律分析

3.1 开口倒角影响分析

从前文计算结果可以看出，虽然采取加强措施后，可一定程度影响结构的应力极值，但从应力极值分布来看主要集中在开口倒角处。下面分析开口倒角的影响规律。开口尺寸不变，不进行结构加强，开口倒角半径分别为0.050 m，0.1 m，0.2 m和0.4 m，采用和前文相同的边界条件和载荷，进行结构分析。表2为位移和应力极值表。

表2 弯曲和扭转状态下不同倒角半径的应力和位移极值

倒角半径对应力极值影响十分明显 （见图4）。弯曲应力和扭转应力都显著降低，当倒角半径由0.4 m变为0.05 m时，弯曲应力增加了80%，扭曲应力增加了133%。图中显示倒角半径对弯扭应力极值的影响，随着倒角半径增加，应力显著降低。

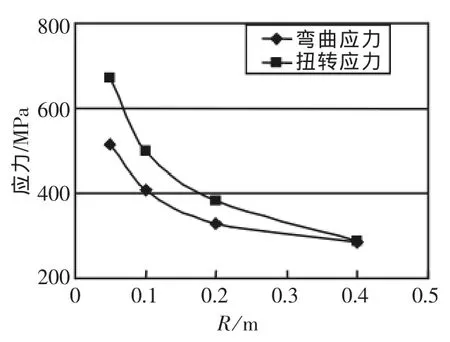
图4 倒角半径对弯扭应力极值的影响

3.2 开口长度影响分析

下面分析开口尺寸对结构弯扭强度的影响，首先分析开口长度的影响。其他参数不变，分别计算开口长度4.65 m，7.65 m和10.65 m时的应力和变形规律。采用和前文相同的边界条件和载荷，进行结构分析。

表3为位移和应力极值表。

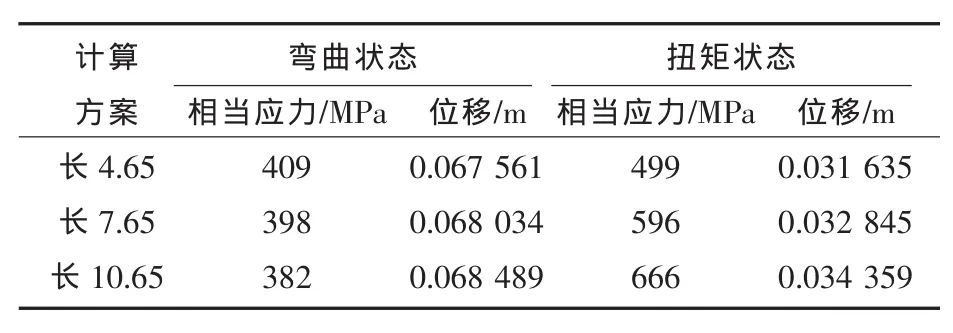
表3 弯曲和扭转状态下不同开口长度的应力和位移极值

开口长度变化对弯曲应力影响不明显。随着开口长度增加，由弯曲应力依次降低了2%和4%，应力极值变化很小。开口长度变化对扭转应力影响明显。随着开口长度由4.65 m增加到7.65 m和10.65 m时，扭转应力分别增加了20%和33%。

增加开口长度，增加甲板的不连续性的同时也增加了横梁的切断数目。由于横梁一般均匀布置，切断横梁占舱段总横梁数比率一方面体现了切断横梁数的影响，同时体现开口长度占舱段甲板长度的比率的影响。图5显示切断横梁比率对弯扭应力极值的影响规律。随着横梁切断比率增加，扭转应力显著增加。

图5 横梁切断比率对弯扭应力极值的影响规律

3.3 开口宽度影响分析

下面分析开口宽度的影响。其他参数不变，分别计算开口宽度2.6 m，6.6 m和10.6 m时的应力和变形规律。采用和前文相同的边界条件和载荷，进行结构分析。

表4为位移和应力极值表。

表4 弯曲和扭转状态下不同开口宽度的应力和位移极值

开口宽度变化对弯曲应力和扭转应力影响明显。随着开口宽度由2.6 m增加到6.6 m和10.6 m时，弯曲应力分别增加了23%和43%，扭转应力分别增加了44%和106%。

增加开口宽度增加了纵骨的切断数目。与横梁切断相似，下面分析纵骨切断比率的影响。图6显示切断横梁比率对弯扭应力极值的影响规律。随着纵骨切断比率增加，弯曲和扭转应力显著增加。

图6 纵骨切断比率对弯扭应力极值的影响规律

3.4 开口尺寸对结构其它位置应力影响

为了分析开口尺寸对结构强度的影响，文中以船体结构的固定位置的应力数值进行对比 （图8、图9）。以开口舱室中间旁舷壁与顶层甲板的交界处为例，具体位置如图7中A点所示。

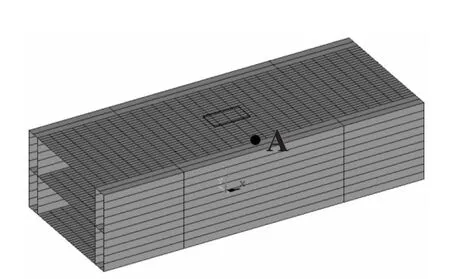
图7 点A的分布位置

分析结果：

1）从图8、图9中可以看出开口宽度对结构的强度影响十分明显。随着开口宽度的增加，A点的弯曲应力和扭转应力都显著增加。

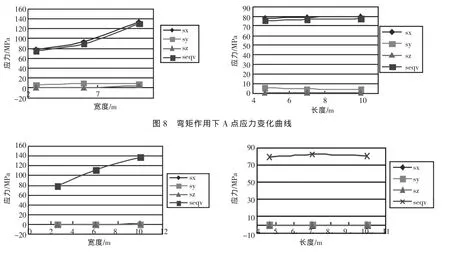
图9 结构扭转作用下A点应力变化曲线

2）从应力变化曲线可以看出，开口长度对A点应力数值影响并不明显。

3）从应力数值来看，结构的危险应力主要集中在结构开口附近，需重点考虑开口附近结构的安全性。

4 结论

文中采用有限元方法对船舶临时开口结构的结构强度和加强方案进行研究，得到如下结论：

1）依据 《中国船级社钢质海船入级规范（2006）》计算，临时开口造成的船体结构的抗弯和抗扭转能力下降，在航行或系泊状态下，如遇极限载荷，船体的结构强度达不到要求，因此必须在开口处进行加强。

2）通过结构开口的参数分析，可得出如下规律：

·倒角半径对应力极值影响十分明显。当倒角半径由0.4 m变为0.05 m时，弯曲应力增加了80%，扭曲应力增加了133%。随着倒角半径的增加，弯曲应力和扭转应力都显著降低。

·沿船长方向的开口长度的变化，对结构弯曲应力影响不明显，却对扭转应力影响明显。随着开口长度由4.65 m增加到7.65 m和10.65 m时，扭转应力分别增加了20%和33%。切断横梁占舱段总横梁数比率研究可知，随着横梁切断比率增加，扭转应力显著增加。

·沿船宽方向的开口宽度的变化，对弯曲应力和扭转应力影响明显。随着开口宽度由2.6 m增加到6.6 m和10.6 m，弯曲应力分别增加了23%和43%，扭转应力分别增加了44%和106%。切断纵骨占舱段总纵骨数比率研究可知，随着纵骨切断比率的增加，弯曲和扭转应力显著增加。

·开口对结构整体应力分布产生影响，危险应力主要分布在开口附近。

以上规律对船厂船体结构临时开口工艺具有重要的工程参考价值。

［1］VALSGARD S，SVENSEN T E，THORKILDSEN H.A computational method for analysis of container vessels［J］.SNAME Trans，1995，103：371-394.

［2］HU Y，JIN X，CHEN B.A finite element model for static and dynamic analysis of thin－walled beams with asymmetric cross－sections［J］.Computers＆Structures，1996，61（5）：897－908.

［3］顾永宁，滕晓青，戴立广，等.大开口船波浪载荷长期预报和弯扭强度整船有限元分析［J］.中国造船，1998（2）：63－70.

［4］刘建成，顾永宁.大开口船舱口角隅应力集中问题研究［J］.船舶工程，2000（6）：9－12.

［5］胡毓仁，陈伯真.大开口船舶的扭转极限状态［J］.上海交通大学学报，2001，35（4）：556－561.

［6］王立军，王伟，叶步永.大开口船舶角隅强度有限元分析研究［J］.浙江海洋学院学报，2007，26（4）：425－428.

［7］黄浩.船体工艺手册［M］.北京：国防工业出版社，1989.

［8］王国强.实用工程数值模拟技术及其在ANSYS上的实践［M］.西安：西北工业大学出版社，1999.

［9］CCS.中国船级社钢质海船入级规范［S］.中国船级社，20 06.

Numerical Analysis of Ship Structures with Cutting Hatch Openings

Zhou Bo1Liu Yu－jun1Duan Hong2Yang Long2Teng Shu－sheng2
1 School of Naval Architecture，Dalian University of Technology，Dalian 116024，China 2 China Ship Development and Design Center，Wuhan 430064，China

In order to analyze the strength of ship structures with cutting hatch openings，in this study，finite element models of ship structure are presented and strength analysis is performed based on correlate ship strength check criterions.The simulation results show that for ship structures with cutting hatch openings，it is necessary to pay attention to the safety in respect of bend and torsion.The variations of stresses and distortions with cutting hatch sizes are also analyzed.This study provides an important reference for engineering application.

ship structure；strength analysis；numerical simulation；hatch opening；bend and torsion；reinforcing designs

U661.43

A

1673－3185（2009）02－28－06

2008-09-26

周 波（1977－），男，博士研究生。研究方向：船舶与海洋结构物制造工艺。E-mail：cam＠dlut.edu.cn

刘玉君（1962－），男，教授，博士生导师。研究方向：舰船与海洋结构物制造工艺