一道几何题的几种解法

黄金旺

几何题往往能一题多变，一题多解.同学们若能经常有目的地进行这类习题的训练，探寻解题思路与方法，掌握灵活多变的解题技巧，亲自感受到获得解题新思路和新方法的愉快感，将有利于自身开拓思维.开发智力，有助于培养自己的创新兴趣和创新能力，现举例分析如下：

题目：正方形ABCD内一点P,∠PAD =∠PDA=15°，连结PB、PC，请问：△PBC是等边三角形吗？为什么？

解法一：

∵∠PAD=∠PDA=15°

∴AP=PD ∠PAB=∠PDC=75°

又∵AB=CD

∴△PAB≌△PDC（SAS）

∴BP=PC

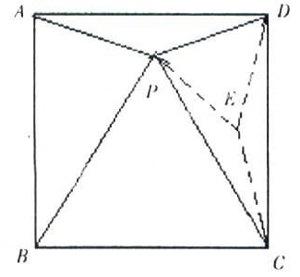
在正方形内作∠EDC=∠ECD=15°，DE与CE交于E点，连结PE，显然∠DEC =150°

∴△APD≌△CED（ASA）

∴DP=DE

∠PDE=∠ADC－∠ADP－∠CDE

=90°－15°－15°=60°

所以，△EDP为正三角形，

∴PD=PE=ED

又∠PEC=360°－（∠PED＋∠DEC）

=360°－（150°＋60°）

=150°

∴∠PEC=∠DEC

∴△DEC≌△PEC（SAS）

∴PC=DC

从而，BP=PC=BC

即：△PBC为等边三角形．

解法二：

以AD为边向外作等边△AED.再连结EP．

∵∠PAD=∠PDA=15°

∴AP=PD

在△EAP和△EDP中

△EAP≌△EDP（SSS）

∴∠1=∠2=60°

在△EAP和△BAP中

EA=AB∠EAP=∠BAPAP=AP=75°

∴△EAP≌△BAP（SAS）

∴∠3=∠1=30°

同理可知：∠PCD=30°

∴∠PBC=∠PCB=60°

即：∠BPC=60°

∴△PBC是等边三角形．

解法三：（反证法）

假设△PBC不是正三角形，由已知条件推得PB=PC

即假设PB=PC≠BC

不妨设PB＞BC，则在△ABP中，∠BAP＞∠APB

即：∠APB＜75°，而∠DPC=∠APB

所以∠DPC＜75°

又∠APD=180°－∠PAD－∠ADP

=150°

所以∠BPC=360 °－（∠APD＋∠APB ＋∠DPC）＞60°

同时在△BPC中，由PB=PC＞BC

∴∠PBC=∠PCB＞∠BPC,得∠BPC ＜60°

这与∠BPC＞60°矛盾，故PB＞BC不能成立

同理PB＜BC也不能成立

故PB＝BC，即△PBC为正三角形．

解法四：（同一法）

以BC为边作正△BEC，连结BE、CE、AE、DE，

则BE＝CE=BC ∠EBC=∠ECB=60°

又∵BC=AB

∴AB=BE

∴∠ABE=90°－∠EBC=90°－60°=30°

∴∠BAE=∠BEA=75°

∴∠EAD=15°

同理可证：∠EDA=15°

因此，EA与PA重合，ED与PD重合

从而，△PBC为正三角形．

除了上述证法外，本题还有其他证法，教师可鼓励学生开拓思维，集思广益考虑出更多的论证方法．