不等式（组）创新性考查方式分类探究

周　芹

一、不等式（组）与现实生活相结合

人们的生活离不开数学，数学也离不开人们的现实生活.除有部分试题直接考查不等式(组)的基本性质外，还有部分试题与现实生活相联系，考查不等式(组)的基本性质的具体运用.

例如，幼儿园把新购进的一批玩具分给小朋友，若每人3件，那么还剩余59件；若每人5件，那么最后一个小朋友分到玩具，但不足4件，这批玩具共有_________件.(答案:152)

二、不等式（组）与输入法相结合

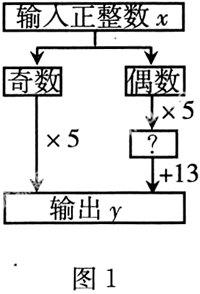
编程输入在电子事业快速发展的今天，越来越被人们青睐.命题者常以此为背景，编制一些形式清新，运算简便，其间还渗透重要数学思想的一些不等式创新题.

例如，如图1，要使输出值y大于100，则输入的最小正整数x是_______.

(答案：18)

三、不等式（组）与方程相结合

一方面，方程与不等式有着不可分割的联系：当两者代数式表明相等关系时，就成了方程；当两者代数式

表明不等关系时，就成了不等式.另一方面，方程与不等式常常联姻，结合方案优劣的选取，分类讨论等重要数学思想综合考查.

例如，青青商场经销甲、乙两种商品，甲种商品每件进价15元，售价20元；乙种商品每件进价35元,售价45元.(1)若该商品同时购进甲、乙两种商品共100件恰好用去2700元，求能购进甲、乙两种商品各多少件？（2）该商场为使甲、乙两种商品共100件的总利润（利润=售价-进价）不少于750元，且不超过760元，请你帮助该商场设计相应的进货方案；(3)在“五•一”黄金周期间，该商场对甲、乙两种商品进行如下优惠促销活动：

按上述优惠条件，若小王第一天只购买甲种商品一次性付款200元，第二天只购买乙种商品打折后一次性付款324元，那么这两天他在该商场购买甲、乙两种商品一共多少件?(通过计算求出所有符合要求的结果)(答案：(1)甲40件，乙60件.(2)有3种方案：方案1，购进甲种商品48件，乙种商品52件；方案2，购进甲种商品49件，乙种商品51件；方案3，购进甲种商品50件，乙种商品50件.(3)在该商场购买甲，乙两种商品一

共18件或19件.)

四、不等式（组）与一次函数相结合

不等式与一次函数相结合又是数形结合思想的重要体现.反映在直接应用上，求不等式kx+b＞0的解集.实际上令一次函数 y=kx+b中的y＞0,表现在图象中,直线在x轴上方的部分对应的x的值,即为所求不等式的解集.

例如,如图2,直线y=kx+b交坐标轴于A、B两点,不等式kx+b＞0的解集是().

A.x＞-2 B.x＞3

C.x＜-2D.x＜3

(答案:A)

本题无需用待定系数法求出k、b,再去解不等式kx+b＞0,如果这样，那么就违背了命题者的真实意图.先利用一次函数关系分别表示两个量，再设置问题情境，列出不等式，实现解决问题的办法.例如，小华准备将平时的零用钱节约一些储存起来，他已存有62元，从现在起每个月存12元.小华的同学小丽以前没有存过零用钱，听到小华在存零用钱，表示从现在起每个月存20元，争取超过小华.(1)试写出小华的存款总数y1与从现在开始的月数x之间的函数关系式以及小丽存款数y2与月数x之间的函数关系式；(2)从第几个月开始小丽的存款数可以超过小华?(答案：(1)y1=12x+62，y2=20x.(2)从第8个月开始.)或由“一次函数霾坏仁(组)的解→二次函数的最值”的过程.