《等腰三角形》测试题

朱睛睛

天才?请你看看我的臂肘吧！

——斯里尼瓦萨•拉马努扬（19世纪、20世纪印度数学家）

一、填空题（每小题3分，共27分）

1． 若等腰三角形周长为30，一条边长为12，则另两边的长为__；若等腰三角形周长为30，一条边长为4，则另两边的长为__.

2． 若等腰三角形的顶角和一个底角的和是110°，则它的一个底角为__.

3． 等腰三角形一腰上的中线把这个三角形的周长分成12 cm和21 cm两部分，则这个等腰三角形的底边长是__.

4． 如图1，在△ABC中，AD⊥BC于D.请你再添加一个条件，使△ABC是等腰三角形.你添加的条件是：__.

5． 如图2，△ABC中，AD⊥BC，D为垂足.点E、F分别是AC、AB上的点，且DF⊥AB，DE⊥AC.要使DF=DE，则图中线段应满足的条件是__.

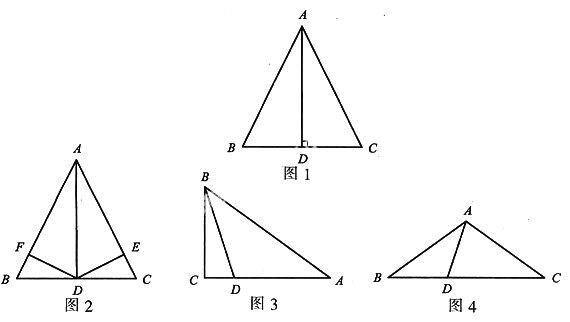
6． 在△ABC中，AB=AC，AB的中垂线与AC所在直线相交所得的锐角为50°，则△ABC的底角为__.

7． 如图3，已知△ABC中，∠C=90°，∠DBC=18°，AD=BD，那么∠A=__.

8． 如图4，△ABC中，D是BC边上的一点，若AD=BD，AB=AC=CD，则∠BAC=__.

9． 如图5，△ABC中，BC边的垂直平分线DE交BC于D，交AC于E.BE=5 cm，△BCE的周长是18 cm，则BD=__.

二、选择题（每小题3分，共27分）

10． 已知等腰三角形两条边的长分别为2和5，则它的周长为（）.

A. 9 B. 12C. 9或12 D. 5

11． 有下列三角形：①有两个角等于60°的三角形；②有一个角等于60°的等腰三角形；③三个外角（每个顶点处各取一个外角）都相等的三角形；④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有（）.

A. ①②③ B. ①②④

C. ①③ D. ①②③④

12． 如图6，△ABC中，∠A=36°，AB=AC，BE平分∠ABC，DE∥BC，则图中有等腰三角形（）.

A. 1个 B. 3个 C. 4个D. 5个

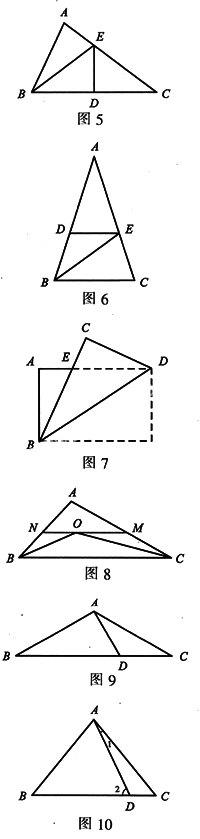
13． 如图7，把矩形纸片ABCD沿对角线BD折叠，设重叠部分为△EBD，那么下列说法错误的是（）.

A. △EBD是等腰三角形，EB=ED

B. 折叠后∠ABE和∠CBD一定相等

C. 折叠后得到的图形是轴对称图形

D. △EBA和△EDC是全等三角形

14． 如图8，△ABC中，BO平分∠ABC，CO平分∠ACB，且MN∥BC.设AB=12，BC=24，AC=18，则△AMN的周长是（）.

A. 30 B. 33 C. 36 D. 39

15． 如图9，已知△ABC中，AB=AC，∠C=30°.AB⊥AD，AD=2.则BC的长为（）.

A. 8 B. 6C. 4 D. 2

16． 如图10，已知D是BC上一点，且有AB=AC=BD，那么∠1与∠2的关系是（）.

A. 3∠2-∠1=180° B. ∠1+2∠2=180°

C. 3∠1+∠2=180° D. ∠1=2∠2

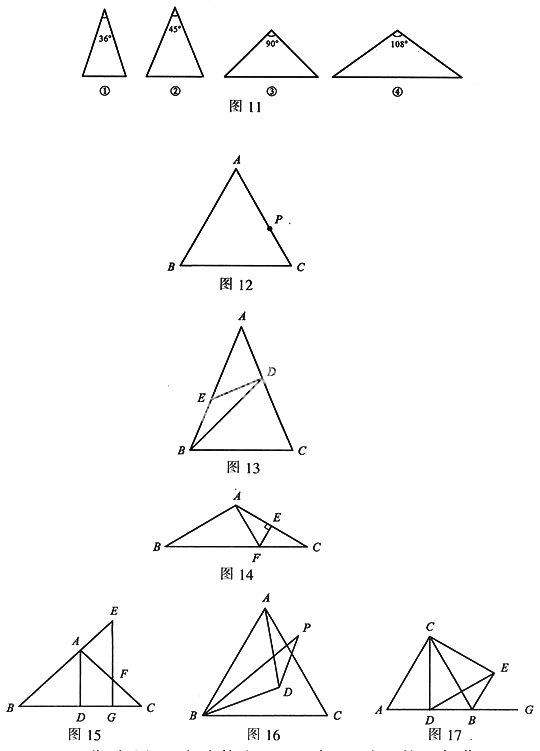
17． 图11中的每个等腰三角形都给出了顶角的度数，其中能被一条直线分成两个小等腰三角形的是（）.

A. ①②③B. ①②④C. ②③④D. ①③④

18． 图12是一个等边三角形木框，甲虫P在边框AC上爬行（端点A、C除外）.设甲虫P到另外两边的距离之和为d，等边△ABC的高为h，则d与h的大小关系是（）.

A. d>h B. d

三、解答题

19． （8分）如图13，在△ABC中，AB=AC，D点在边AC上，且BD=BC.E点在边AB上，AD=DE=EB.求∠EDB.

20． （8分）如图14，△ABC中，AB=AC，∠BAC

=120°.AC的垂直平分线EF交AC于点E，交BC于点F.求证：BF=2CF.

21． （8分）如图15，在△ABC中，AB=AC，点D是BC边的中点，E是BA延长线上一点，F是AC上一点，且AE=AF.连接EF并延长，交BC于G.则AD与EG平行吗？为什么？

22． （10分）如图16，D为等边△ABC内的一点，BP=AB，∠DBP=∠DBC，∠BPD=30°.试判断△ABD的形状，并说明理由.

23． （10分）如图17，D为等边△ABC中AB边上的一点.作∠CDE=60°，DE交∠ABC的补角的平分线于点E .试证明△CDE是等边三角形.

四、拓展题

24． （10分）如图18，△ABC是边长为1的等边三角形，BD=CD，∠BDC=120°.E、F分别在AB、AC上且∠EDF=60°.求△AEF的周长.

25． （12分）如图19，以△ABC的两边AB、AC为边向外作等边三角形ABD和ACE，DC、BE相交于点O.

（1）求证：DC=BE.

（2）求∠BOC.

（3）∠BAC的大小发生变化时，∠BOC是否变化？若不变化，请求出∠BOC；若发生变化，请说明理由.