全等三角形开放型问题评析

李厚明

全等三角形是几何的重要学习内容，新课标要求同学们对全等三角形的性质和判定要能够灵活运用.形式多变的全等三角形开放型问题在中考中屡屡出现，下面举例加以解析.

例1如图1，点D、E分别在线段AB、AC上，BE、CD相交于点O，AD=AE.要使△ABE≌△ACD，需添加的一个条件是__（只要写一个即可）．

分析：在添加条件之前，我们首先要弄清楚问题中已有哪些条件.

本题中已有AD=AE及∠A=∠A，对照不同的判定方法，我们可以选择不同的添加方法：

方法一：用“边角边”证△ABE≌△ACD，需添加AB=AC或BD=CE.

方法二：用“角角边”证△ABE≌△ACD，需添加∠B=∠C或∠AEB=∠ADC或∠CEO=∠BDO.

解：∠B=∠C，∠AEB=∠ADC，∠CEO=∠BDO，AB=AC，BD=CE等，任选一个即可.

点评：本题属条件开放型题.补好条件后需检验是否能证到结论.尤其要注意，两边和其中一边的对角对应相等的两个三角形不一定全等（俗称“边边角”）.本题有同学添加CD=BE，这是不正确的.

例2如图2所示，AC、BD相交于点O，AC=BD.试添加一个条件，使得△AOB≌△DOC.添加的条件是__（只需写一个）.

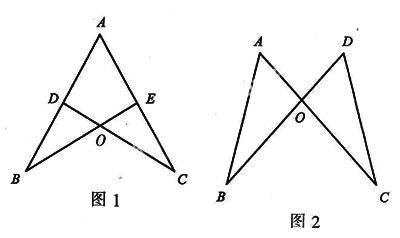
分析：△AOB与△DOC中，只有∠AOB=∠DOC.还差两个条件才能证明全等.题中给出的AC=BD不能直接用上，所以添加的条件除了本身可以用之外，还要能将AC=BD转化为可用条件，所以本题添加的条件须是边.可添加OA=OD或OB=OC.如先证△ABC≌△DCB再证△AOB≌△DOC，则可添加AB=DC.

解：可以填OA=OD或OB=OC或AB=DC等.

点评：本题与上题相比较，由于所给条件不可直接用，所以所添条件的空间不大.这就要求我们认真审题，重视从原有条件出发，千万不能随意添加.

例3如图3所示，在△ABC与△ABD中，AD与BC相交于点O，∠1=∠2.请你添加一个条件（不再添加其他线段，不再标注或使用其他字母），使AC=BD，并给出证明.你添加的条件是：__.

分析：本题要证AC=BD，需证△ABC≌△BAD或△AOC≌△BOD.而△AOC和△BOD中除一对对顶角相等以外，无其他条件可用，不易入手.△ABC和△BAD中除∠1=∠2外，尚有公共边AB.考虑SAS可添加AD=BC；考虑ASA可添加∠CAB=∠DBA或∠CAD=∠DBC；考虑AAS可添加∠C=∠D.

解：填AD=BC（或DO=CO）或∠CAB=∠DBA或∠CAD=∠DBC或∠C=∠D等 .证明略.

点评：本题看上去全等的三角形不止一对，所以对解题有一定的干扰.从条件较多的一对三角形中添加条件无疑是明智之举.

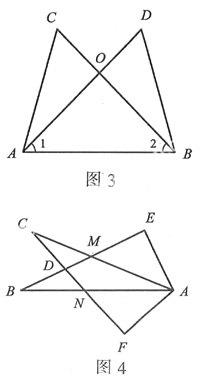
例4如图4所示，∠E=∠F=90°，∠B=∠C，AE=AF.给出下列结论：（1）∠EAM=∠BAF；（2）BE=CF；（3）△ACN≌△ABM；（4）CD=DN.其中正确的结论有__（只需填序号）.

分析：本题属结论开放型问题，可从已知条件出发推演.由∠E=∠F=90°，∠B=∠C，可证得△AEB≌△AFC（AAS），得到BE=CF，AC=AB及∠EAB=∠FAC，从而得∠EAM=∠BAF，所以（1）、（2）成立.由AC=AB，∠B=∠C以及公共角∠CAN=∠BAM，可证△ACN≌△ABM，所以（3）成立.而CD、DN不是全等三角形的对应边，也不能从其他条件证得，所以（4）不成立.

解：填（1）、（2）、（3）.

点评：关于全等三角形的结论开放型题，由于结论的不确定性，需我们一个一个地仔细判别.尤其要注意，一些结论比较隐蔽，需经过两次或两次以上的全等才能得到.那些图形上看像正确而你又推不出的结论，一定要认真对待噢！