巧用旋转变换解题

丁广琳

将一个图形旋转，图形上的每一个点都绕着中心沿着相同的方向转动了相同的角度.任意一对对应点与旋转中心的连线所成的角都是旋转角，对应点到旋转中心的距离相等；旋转前后的两个图形是全等形，对应边、对应角都相等.另一方面，一些图形又可看成是由一个图形旋转而成的.这些特点都给解题创造了有利的条件.

一、利用旋转的基本性质解师

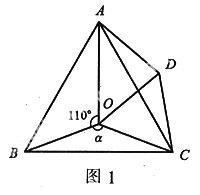
例1（2007年·宁德）如图1所示，点O是等边△ABC内一点，∠AOB=110°，∠BOC=α．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．

（1）求证：△COD是等边三角形.

（2）当α=150°时，试判断△AOD的形状，并说明理由.

（3）探究：当α为多少时，△AOD是等腰三角形？

解析：可以利用旋转的基本性质，找出旋转前后的对应线段、对应角.抓住旋转前后的图形是全等形这一性质进行解题.

（1）CO=CD，∠OCD=60°，故△COD是等边三角形．

（2）当α=150°，即∠BOC=150°时，因△BOC≌△ADC，故∠ADC=∠BOC=150°.又△COD是等边三角形，故∠ODC=60°．所以∠ADO=90°．△AOD是直角三角形．

（3）首先，∠AOD=360°-110°-60°-α=190°-α，∠ADO=α-60°.若△AOD是等腰三角形，按每两边相等可以有三种情况：

①要使AO=AD，需∠AOD=∠ADO．故190°-α=α-60°. α=125°.

②要使OA=OD，需∠OAD=∠ODA．因∠OAD=180°-（∠AOD+∠ADO）=180°-（190°-α+α-60°）=50°，∠ODA=α-60°，所以α-60°=50°． α=110°．

③要使DO=DA，需∠OAD=∠AOD．所以（由②的一个结论）50°=190°-α. α=140°．

综上所述，当α为125°，110°或140°时，△AOD是等腰三角形．

二、利用旋转整合图形解题

在解决几何问题时，常常将某个图形旋转一定的角度，通过这种旋转对图形进行割补，把不规则图形整合为规则图形，使问题的条件由分散变得相对集中，从而顺利解决问题.

例2如图2，在正方形ABCD中，P、Q分别是BC、CD上的点，∠PAQ=45°.试说明BP+DQ=PQ.

解析：如图3，将△ADQ绕A点顺时针方向旋转90°到△ABE，由旋转的基本性质：

∠EAB=∠QAD，BE=DQ，

∠EAQ=∠BAD=90°.

所以，∠EAP=45°=∠PAQ.

由于AD=AB，∠EBA=∠D=90°，所以E、B、P三点在一条直线上.易知△EAP≌△QAP（SAS），所以PQ=PE.而PE=BP+BE，所以BP+DQ=PQ.

三、旋转变换与作图

利用旋转的基本性质作图，是中考中出现频率较高的题型.解题关键还是要抓住旋转过程中的不变量.

例3（2007年·云南）如图4，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：

（1）作出格点△ABC关于直线DE对称的图形△A1B1C1；

（2）作出△A1B1C1绕点B1顺时针方向旋转90°后的图形△A2B2C2 .

解析：略.

四、中考链接，请你试一试

1． （2007年·西安）如图5，在等边△ABC中，AC=9.点O在AC上，且AO=3.点P是AB上一动点.连接OP，将线段OP绕点O逆时针方向旋转60°得到线段OD．要使点D恰好落在BC上，则AP的长是（）.

A． 4 B． 5 C． 6 D． 8

答案：C

提示：注意到这时将会有△PBD≌△OAP（AAS），BP=AO=3.

2. （2007年·徐州）如图6，将两张相同的正方形纸片完全重合地叠放在一起，中心都是点O.按住下面的纸片不动，将上面的纸片绕点O顺时针方向旋转15°，所得重叠部分的图形（）.

A. 既不是轴对称图形也不是中心对称图形

B. 是轴对称图形但不是中心对称图形

C. 是中心对称图形但不是轴对称图形

D. 既是轴对称图形也是中心对称图形

答案：D

3. （2007年·衢州）一副三角板按图7所示叠放在一起.现固定△AOB，将△ACD绕着公共顶点A，按顺时针方向旋转α角（0°<α<180°）.当△ACD的一边与△AOB的某一边平行时，相应的旋转角α是___.

答案：30°，45°，75°，135°，165°

提示：AC只能平行于BO，AD只能平行于BO，CD可平行于△AOB的三边.