高校智力资本的测量

　　【摘要】在知识经济时代，组织中最具价值、最稀缺的资源是智力资本，同时智力资本又是获取持续性竞争优势的关键。本文对高校智力资本的测量方面进行了有益的探索，提供了一个相对完善的智力资本测量体系。
　　
　　国际上对智力资本的测量以及更进一步提供规范化报告的研究还处于探索阶段，离实务应用还有着相当的差距。国内对智力资本研究仍处于引进与学习国外新颖、先进方法的初级阶段。对于智力资本的测量，根据所用的测量指标可以分为：财务测量法和绩效测量法；根据测量的结构体系可以分为：逐项测量法和整体测量法。逐项测量法是指逐项测量智力资本的每个项目，然后进行汇总的一种方法；整体测量法是基于组织智力资本的整体，利用其市场价值与账面价值的差值来确定智力资本的价值。对于高校而言，由于很难确定其市场价值，因此笔者采用逐项绩效测量法来进行高校智力资本的测量，然后再加以汇总。即先确定高校智力资本三个层面及其对应指标的权重；然后利用这些指标的历史数据进行标准化和分值化处理；最后进行各项分值的汇总。
　　由于高校智力资本的三个层面及其相应的指标具有不同的内涵，对它们重要性的估计就存在着不确定性，直接表现为众说纷纭，在重要性的排序上各执一词，在定量上莫衷一是。笔者在确定高校智力资本三个层面及其指标的权重时，引进了权系数层次分析法。
　　
　　一、高校智力资本测量框架的构建
　　
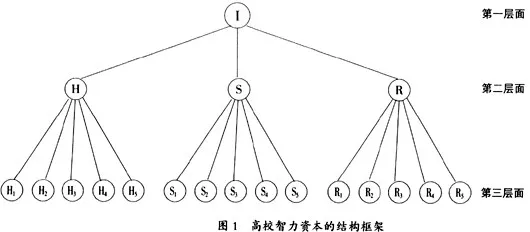
　　本文研究的高校智力资本的测量框架是阶梯层次的结构框架，分为三个层次。第一层是高校智力资本；第二层是高校智力资本的三种不同构成；第三层是高校智力资本三种不同构成的具体指标体系，这样就构成了如图1所示的高校智力资本的测量框架。
　　图1中，I表示高校智力资本，H表示高校人力资本，S表示高校结构资本，R表示高校关系资本；H i表示高校人力资本中的第i个指标，S i表示高校结构资本中的第i个指标，Ri表示高校关系资本中的第i个指标。
　　
　　二、高校智力资本的三个层面及其对应指标权重的确定
　　
　　一个高校在不同时期的战略重点会有所不同。因此，智力资本的三个层面及其对应的指标也有轻重缓急。目前，指标体系评估方法分为两类。一类是倾向于客观的方法；一类是倾向于人的主观判断的方法。笔者在此举出有代表性的两种方法——神经网络方法和权系数层次分析法来进行比较。
　　
　　神经网络的方法比较适合解决复杂的非线性问题，因为它需要通过数据的训练来实现任意的非线性映射，所以运用神经网络的方法需要有大量的数据。但是，目前在智力资本测量这个领域中，还没有大量成型的数据。因此，本文不采用这种方法。
　　权系数层次分析法是美国著名运筹学家、匹丝堡大学的T·L·Satty教授于20世纪70年代中期提出的一种系统分析方法。它将一个复杂问题中的各种因素通过划分相互联系的有序层次而使之条理化，根据对一定客观现实的判断，就每一层次的相对重要性给予定量表示，利用数学方法确定表达每一层次的全部元素的相对重要性次序的数值，并通过排序结果分析和解决问题。这种方法能够统一处理决策中的定性和定量因素，具有高度的逻辑性、系统性、简洁性和实用性等优点。因此，本文采用此方法以确定智力资本三个层面及其对应指标的权重。
　　AHP分析模型的计算步骤如下：
　　
　　（一）对相关部门的专家进行问卷调查
　　内容包括：
　　1.对高校智力资本的三个层面：高校人力资本、高校结构资本和高校关系资本的重要性进行两两比较；
　　2.对高校人力资本的五个具体指标的重要性进行两两比较；
　　3.对高校结构资本的五个具体指标的重要性进行两两比较；
　　4.对高校关系资本的五个具体指标的重要性进行两两比较。
　　针对以上四个方面内容的调查表使用选择法，供选择的答案包括以下九个：
　　A.重要程度相同
　　B.略重要
　　C.重要
　　D.重要很多
　　E.第一个非常重要，第二个根本不能与之相比
　　F.界于A与B之间
　　G.界于B与C之间
　　H.界于C与D之间
　　I.界于D与E之间
　　
　　（二）对调查结果进行赋值，计算三个层面及其对应指标的权重
　　1.在对收集的成对调查结果进行赋值时，采用以下九级分制
　　设a和b为两个指标，将它们的重要程度之比记作a / b并给予数值，记作a / b:＝。则九级分制可以说明如下：
　　a / b：＝说明
　　1 a与b重要程度相同
　　3 a比b略重要
　　5 a比b重要
　　7 a比b重要很多
　　9 a非常重要，b根本不能和它比
　　2，4，6，8赋值在相邻两整数之间折中
　　1 / n（n＝1，……9） 当b / a：＝n时
　　2.计算高校智力资本三个层面的权重
　　对上述调查反馈结果进行整理统计。将每一个调查对象对高校人力资本、高校结构资本和高校关系资本三个方面的成对比较结果按九级分制进行赋值，用一个判断矩阵描述出来。判断矩阵模式如下：
　　
　　其中，各符号含义如下：
　　H－高校人力资本；S－高校结构资本；R－高校关系资本。
　　根据调查表对重要性的不同判断计算出该矩阵对应元素的几何平均值，得到一个判断矩阵，再解出该矩阵的最大特征值 λmax，然后进行该判断矩阵的一致性检验，检验步骤如下：
　　（１） 计算该判断矩阵的一致性指标CI
　　CI=λ（max-n） / （n-1）（式2）
　　上式中，n是该判断矩阵的阶数。
　　（２）计算随机性指标RI的值，AHP的随机性指标RI的值在表1中列出：
　　
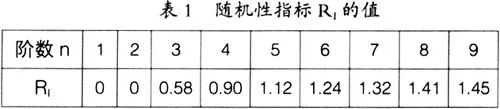
　　随机性一致性比率CR ＝ CI / RI，当CR<0.10时，认为判断矩阵具有满意的一致性，否则要对上述判断矩阵重新调整，直到具有满意的一致性为止。
　　最大特征值所对应的特征向量为W，W经过标准化后，即为高校人力资本、高校结构资本和高校关系资本对高校智力资本的相对重要性的权重。
　　3.计算高校人力资本层面所对应的指标的权重
　　对上述第二项调查内容的反馈结果进行整理统计。将每一位调查对象对全校师生比等五项指标的重要性成对比较结果，按九级分制进行赋值，用一个判断矩阵描述出来，矩阵模式如下所示：
　　
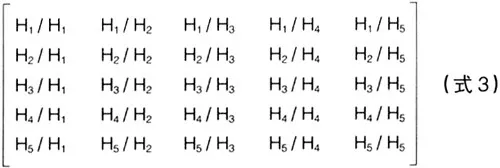
　　计算出该矩阵对应元素的几何平均值，得到一个逆称矩阵，解出该矩阵的最大特征值λmax，再用上述方法判断该矩阵是否具有满意的一致性，然后计算出该最大特征值所对应的特征向量，即为这五个指标对其上层（高校人力资本）的权重。
　　4.计算高校结构资本层面所对应的指标的权重
　　对上述第三项调查内容的反馈结果进行整理统计。将每一位调查对象对省部级及以上科研项目资助金额等五项指标的重要性的成对比较结果，按九级分制进行赋值，用一个矩阵描述出来，矩阵模式如下：
　　
　　
　　计算出该矩阵对应元素的几何平均值，得到一个逆称矩阵，解出该矩阵的最大特征值 λmax，再计算出该特征值的特征向量，即为这五个指标对其上层（高校结构资本）的权重。
　　5.计算高校关系资本层面所对应指标的权重
　　对上述调查内容的反馈结果进行整理统计。将每一位调查对象对学生满意度等五项指标的重要性的成对比较结果，按九级分制进行赋值，用一个矩阵描述出来，矩阵模式如下：
　　
　　计算出该矩阵对应元素的几何平均值，得到一个逆称矩阵，解出该矩阵的最大特征值 λmax，再计算出该特征值的特征向量，即为这五个指标对其上层（高校关系资本）的权重。
　　至此，本研究的高校智力资本的三个层面对高校智力资本的权重以及具体的指标对其上一层的权重已经算出，再根据权系数合成原理，求出第三层指标对最高层（高校智力资本）的权重。
　　
　　三、高校智力资本的绩效测量
　　
　　本研究对某高校的智力资本进行了绩效测量，选取了该高校2001－2005年智力资本相关指标及相关历史数据，以进行纵向业绩的测量和评定，并计算出它们的平均值及标准差，然后按以下步骤计算各指标的分值：
　　（一）确定指标的方向性
　　指标分为正向指标和逆向指标，前者越高越好，后者越低越好。
　　（二）进行标准化处理
　　把不同计量单位的指标值，改为无量纲数值。其计算公式为：yi＝（Xi－X） / SD（式6）
　　其中，Xi是评价指标的本期实际值，X是该指标的平均值，SD是该指标所有样本数的标准差。
　　（三）标准化的结果分值化
　　正向指标以标准化的结果为分值，逆向指标以标准化的结果乘以“-1”为分值。
　　（四）计算单项指标分值
　　即按各指标的权重对上一步分值化的结果进行调整，求出分值化结果与权重的乘积。
　　（五）计算各方面的分值及总分值
　　将各层面的各指标分值加总，得到反映该层面绩效的分值。将三个层面的分值加总，即得到该高校智力资本综合绩效的分值。
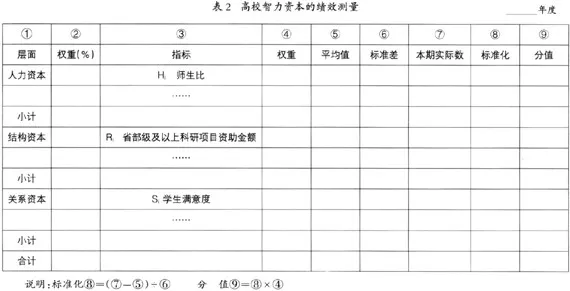
　　对于测量的实际运用详见表2。