管道在水平定向钻施工及服役期的力学响应分析

摘要：

水平定向钻穿越管道在施工及服役期的力学响应受到多种因素的影响，现有理论和计算方法均在很大程度上受限于经验修正参数的选择。基于现场实测数据，通过有限元数值模拟对钢管在水平定向钻施工回拖过程中的受力变形及在外部压力作用下的结构稳定性进行研究。模拟结果表明：在回拖过程中，钢管在出土端的Mises应力和纵向弯矩明显大于入土端；在钻孔的弯曲段，钢管的Mises应力和纵向弯矩均随着弯曲段曲率半径的减小而增大；当钢管在外部压力作用下发生结构屈曲失稳时，塑性应变主要集中在管道的顶部、底部及两侧位置处，其所能承受的外部压力随着管道壁厚的增大而增大，随着直径的增大而减小。

关" 键" 词：

水平定向钻； 钢管； 施工回拖； 结构稳定性

中图法分类号： TV314

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2025.01.027

收稿日期：2024-02-07；接受日期：2024-04-30

基金项目：

浙江省基础公益研究计划项目（LGG20E080005）

作者简介：

郑" 华，男，高级工程师，主要从事管道非开挖施工技术研究。E-mail：zhenghua20230810@126.com

Editorial Office of Yangtze River. This is an open access article under the CC BY-NC-ND 4.0 license.

文章编号：1001-4179（2025） 01-0198-07

引用本文：

郑华.管道在水平定向钻施工及服役期的力学响应分析

［J］.人民长江，2025，56（1）：198-204.

0" 引 言

水平定向钻技术作为一种高效、环保、经济的施工方法，已在石油、天然气、水、电缆和通信线路等地下管道设施的铺设和维修中得到广泛应用。在水平定向钻回拖过程中，管道将承受拉伸、压缩和弯曲等多种受力形式的复合作用，这可能导致管道结构发生扭曲变形而失效破坏。此外，在管道服役期间，其在高静水压力的作用下还可能进一步发生结构的屈曲失稳［1-2］。随着水平定向钻技术的不断进步，管道直径和钻孔长度逐渐增大，管道受力情况更为复杂。

前人针对水平定向钻穿越管道在施工及服役期间的受力变形已经进行了较为深入的研究，提出了多种经验［3-6］或半经验性［7-9］的理论计算方法。然而，由于水平定向钻穿越的工程地质条件复杂多变，因此在理论计算中不得不引入大量的经验修正参数，而经验修正参数的选择不确定性又会很大程度上降低理论计算方法的准确可靠性，限制了其工程应用［10-12］。随着计算机技术的发展，数值模拟计算正逐渐成为研究水平定向钻穿越管道在施工和服役期间受力变形的重要工具。蔡亮学［13］认为，管道在水平定向钻施工过程中的回拖力主要取决于管-土摩擦力，其大小与管-土摩擦系数、管道重量、回拖过程中导向孔方向的改变以及泥浆性能等因素密切相关。郭晓军［14］基于工程实例开展有限元数值模拟分析，指出在管道内部充填液体不仅可以有效减小管道的回拖力，还可以显著提高管道的抗失稳安全系数。石贤增等［15］通过有限元数值模拟研究，发现管道的回拖力随着扩径比和弯曲段曲率半径的增大而减小，指出宜将扩径比和弯曲段曲率分别控制在1.5～1.6和1 300～1 400 m的范围内。以上研究表明，数值模拟分析在水平定向钻技术的研究与应用中已发挥着重要作用，可用于评估和优化水平定向钻穿越管道工程中的各种问题。

本文以江苏沿海如东—常熟—太仓输气管线工程为例，利用现场实测数据开展有限元数值模拟，对管道在水平定向钻施工和服役期间的力学响应特征进行分析，以期为管线的安全运营提供重要的理论依据和设计支持。

1" 工程概况

如东—常熟—太仓输气管线工程在穿越河流时采用水平定向钻技术进行铺设，穿越地层深度为35 m，穿越长度为1 567 m。钢管采用X-65热轧钢板，其直径D和壁厚t分别为1.02 m和26 mm，钻孔直径为1.5D，在转弯处的曲率半径为1 500D，钢管入土角和出土角分别为8°和10°，如图1所示。在回拖过程中，由于钢管的有效浮力大于2kN/m，根据SY/T 6968—2021《油气输送管道工程水平定向钻穿越设计规范》［16］，应采取浮力控制措施。因此，通过在钢管内部安装PE管道，并在PE管道内部充水进行配重降浮。在配重降浮后，钢管的有效浮力为其所受浮力减去自身重力，再减去用于配重降浮的PE管道及其内部充水总重力。经计算，配重降浮后钢管的有效浮力为1.76 kN/m，钢管的回拖速度控制在0.05 m/s。

2" 数值模拟

2.1" 钢管回拖过程数值建模分析

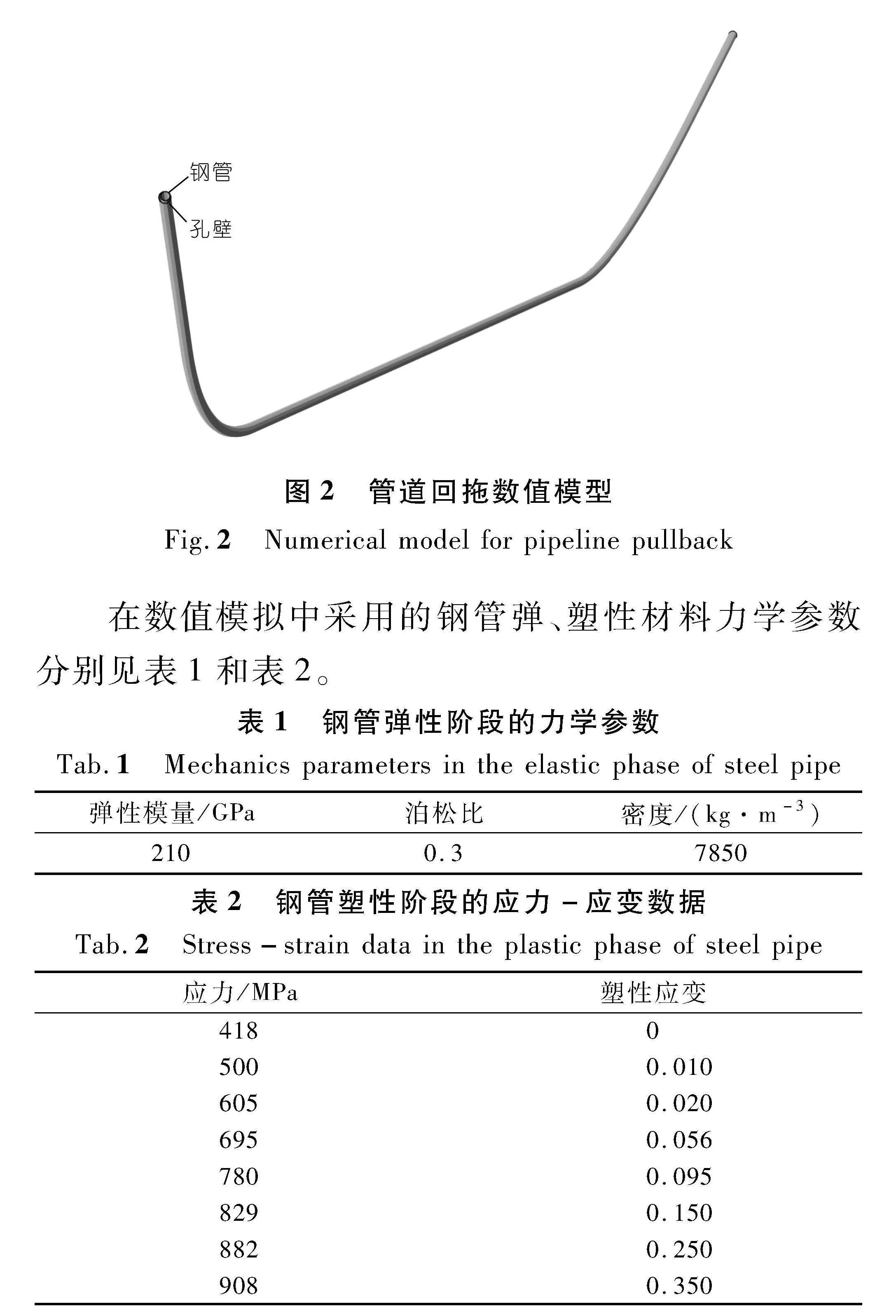
本文使用有限元软件ABAQUS进行数值模拟分析，采用4节点缩减积分壳单元对管道和钻孔壁进行模拟，沿着管道和钻孔壁的环向均匀划分了10个单元，单元网格的纵向尺寸与环向保持一致，以避免单元网格由于扭曲畸变而引起的计算不收敛。实际工程中，对钢管进行配重降浮后其依旧受到向上的浮力作用（即1.76 kN/m），因此在数值建模的初始状态，将钢管紧贴于孔壁的上部，如图2所示。其中，管道和孔壁的几何尺寸与实际工况保持一致。

在建模时将孔壁简化为刚体，即不考虑管道回拖对孔壁的扰动作用。采用这一假定能有效减少模型中的变量和参数，进而降低计算复杂度，使分析过程更高效。然而，在管道回拖的过程中，实际上钻孔壁会受到一定程度的挤压和变形，而导致管道遭遇额外的摩擦力和挤压力。忽略孔壁的变形将无法考虑这一因素的影响，从而低估了管道受到的回拖阻力。但另一方面，忽略孔壁的变形也会增大管道在钻孔弯曲段所受到的绞盘效应，导致管道的回拖阻力计算结果偏大。考虑到在实际工程中钢管的回拖速度仅为0.05 m/s，对孔壁的扰动相对较小［17-18］，因此在该特定条件下，这一简化假定具有一定的合理性。

在数值模拟中采用的钢管弹、塑性材料力学参数分别见表1和表2。

本文所采用的数值模拟计算共分为2个分析步：

（1） 对钢管施加向上的竖向荷载，以模拟钢管在配液减阻后所受到的浮力，并固定孔壁的所有自由度。对于钢管和孔壁之间的切向接触，采用罚函数进行定义，将摩擦系数取为0.3，而法向接触则采用硬接触进行模拟。

（2） 在出土端对钢管施加位移荷载，并控制管道的回拖速度为0.05 m/s。同时，为模拟泥浆对于钢管的黏滞阻力，沿着钢管外表面施加纵向拖拽力（取0.175 kN/m2）［3］。对钢管施加的荷载边界条件如图3所示。

2.2" 钢管结构屈曲稳定性数值建模分析

在回拖结束后，由于地表与地下水系连通，钻孔内的水压力长期处于较高的水平，因此，钢管在服役期间将长期受到高静水压力的影响。在这种情况下，由于钢管受到向上的浮力作用，因此在建模的初始状态同样将管道紧贴于孔壁的上部，并将孔壁简化为刚体，即不考虑孔壁的扰动变形，如图4所示。

在数值模拟中，分别采用4节点缩减积分平面应变单元和2节点刚体单元对管道和钻孔壁进行模拟，沿着管道和钻孔壁的环向均匀划分了40个单元，沿着管道的径向均匀划分了5个单元。为模拟钢管所受到的静水压力，对钢管壁外表面施加沿竖向线性变化的法向压力，即在管道顶部和底部位置处施加的法向压力分别为ρgh和ρg（h+D），其中，h为管道顶部距地下水位的距离，D为管道直径。管道其余位置处的法向压力则在这一范围内随着深度的增大而线性增大，并将孔壁的所有自由度进行固定，如图5所示。对于钢管和孔壁之间的切向和法向接触，则同样分别采用罚函数和硬接触进行模拟。

3" 数值模拟验证

在对水平定向钻施工期和服役期管道受力变形进行数值模拟分析时，数值计算结果与实测结果之间的误差可能源自多个方面：

（1） 参数不确定性。由于施工条件、地质情况等因素的变化，模拟过程中所使用的参数（如摩擦系数、浮力取值、泥浆阻力等）均是基于经验或文献的估计值，从而导致模拟结果与实测结果之间存在误差。

（2） 模型假设的局限性。数值模拟过程中常常需要对现实情况进行简化和理想化处理，比如将钻孔壁简化为刚体，以便于建立数值模型进行计算分析。这些假设可能会忽略一些细节和复杂因素，例如管道与地层之间的非线性接触、管道的非均匀性等，从而引入误差。

在钢管回拖过程中，本文通过数值模拟计算所得到的管道回拖力为1 370 kN，工程实测值为1 400 kN，两者的相对差异仅为2.1%。同时由于回拖结束后，在钢管服役期间并没有对其结构屈曲应力进行测量，因此采用Yan等［19］所报道的模型试验结果对该部分的数值模型进行验证。Yan等［19］将新型热塑性PVC材料用作市政排水管道的内衬修复管材，并通过室内模型试验对PVC内衬管在外部压力作用下的结构屈曲稳定性进行了研究，结果表明当外部压力增加至51 kPa时，PVC内衬管将发生结构屈曲破坏。而本文通过数值模拟所得到的PVC内衬管结构屈曲外部压力为48 kPa，与模型试验实测值的相对误差仅为5.8%。这表明本文所建立的两个数值模型均可以满足对于管道在施工回拖过程中和服役期间力学行为特征的模拟研究。

4" 参数敏感性分析

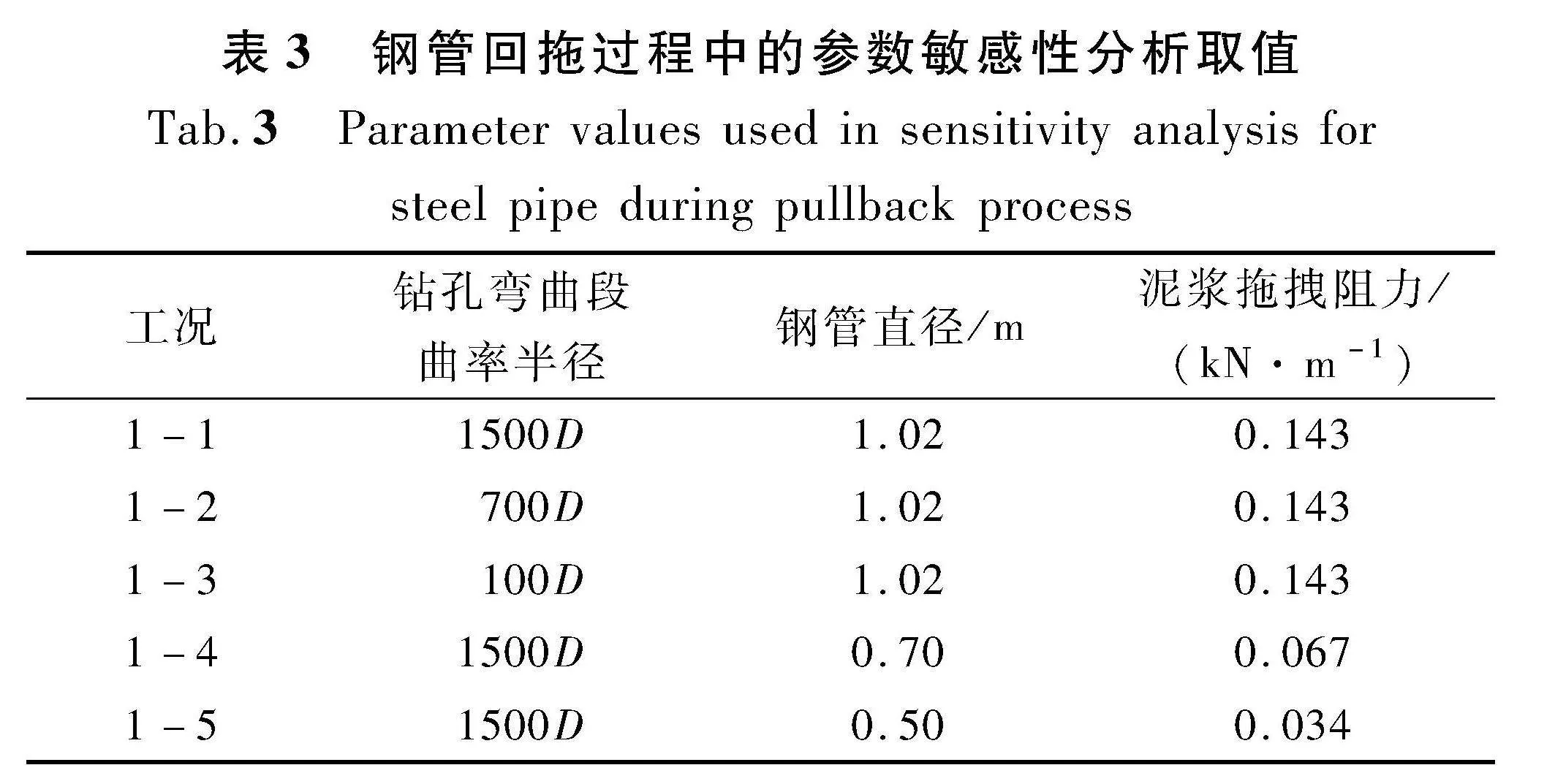
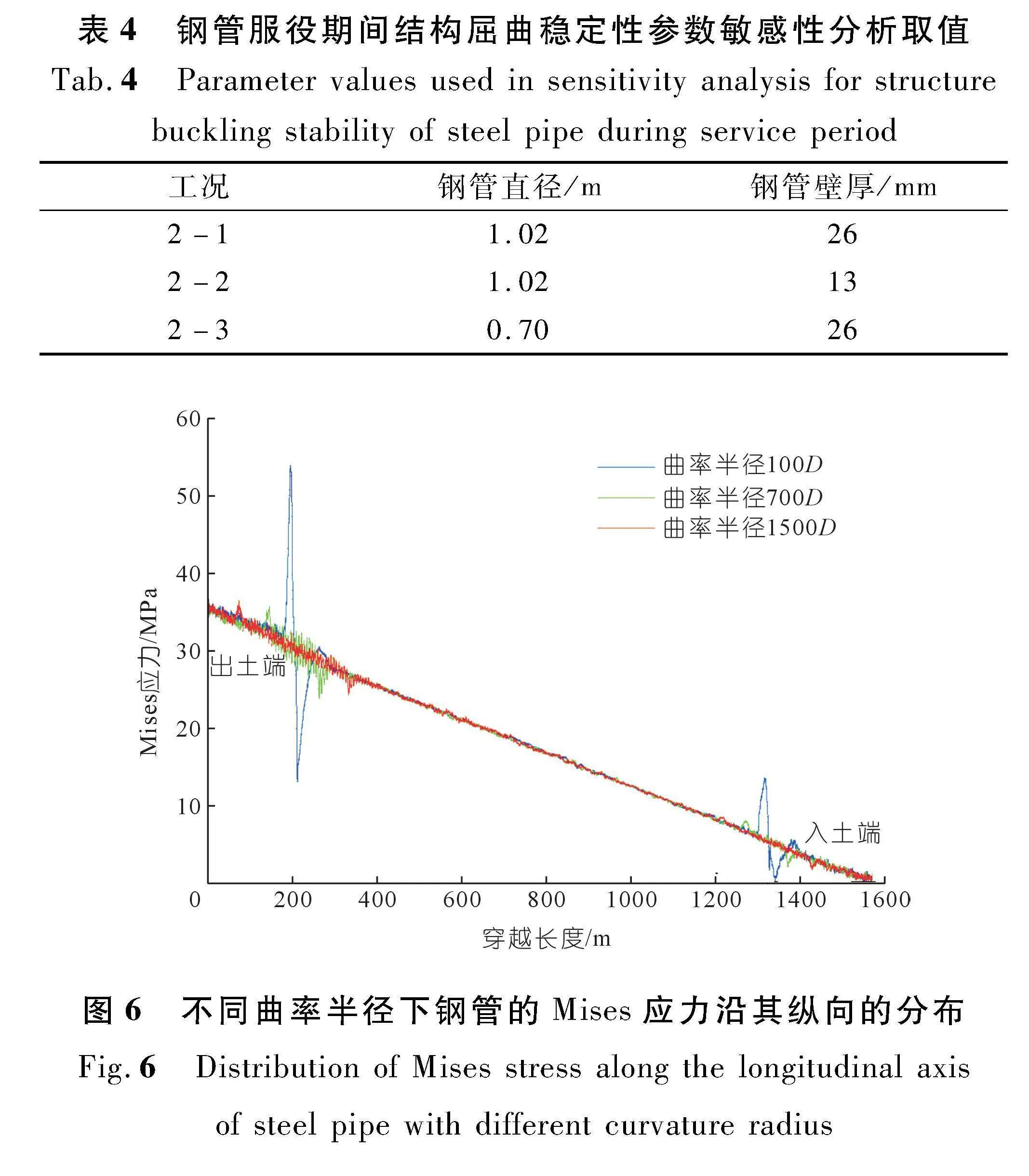
钢管在施工和服役期间的受力变形受到诸如钻孔弯曲段曲率半径、管道直径和壁厚等因素的影响。本文在参数敏感性分析中对于不同变量的取值分别见表3和表4。

5" 数值结果分析

图6为在钻孔弯曲段不同曲率半径下（工况1-1、1-2和1-3），钢管的Mises应力沿其纵向的分布。从图中可以看出，Mises应力从出土端到入土段大致呈线性递减趋势，这是由于回拖力被施加在钢管的出土端而导致的。此外，在钻孔的弯曲段，Mises应力随着弯曲段曲率半径的减小而增大；而在钻孔的直线段，弯曲段曲率半径的变化则对于钢管Mises应力的影响较小。

图7为在钻孔弯曲段不同曲率半径下（工况1-1、1-2和1-3），钢管的纵向弯矩分布。从图中可以看出，在钻孔的弯曲段，钢管的纵向弯矩随着弯曲段曲率半径的减小而增大；而在钻孔的直线段，弯曲段曲率半径对于钢管纵向弯矩的影响较小。此外还可以看出，钢管在出土端的纵向弯矩明显大于其在入口端的纵向弯矩。

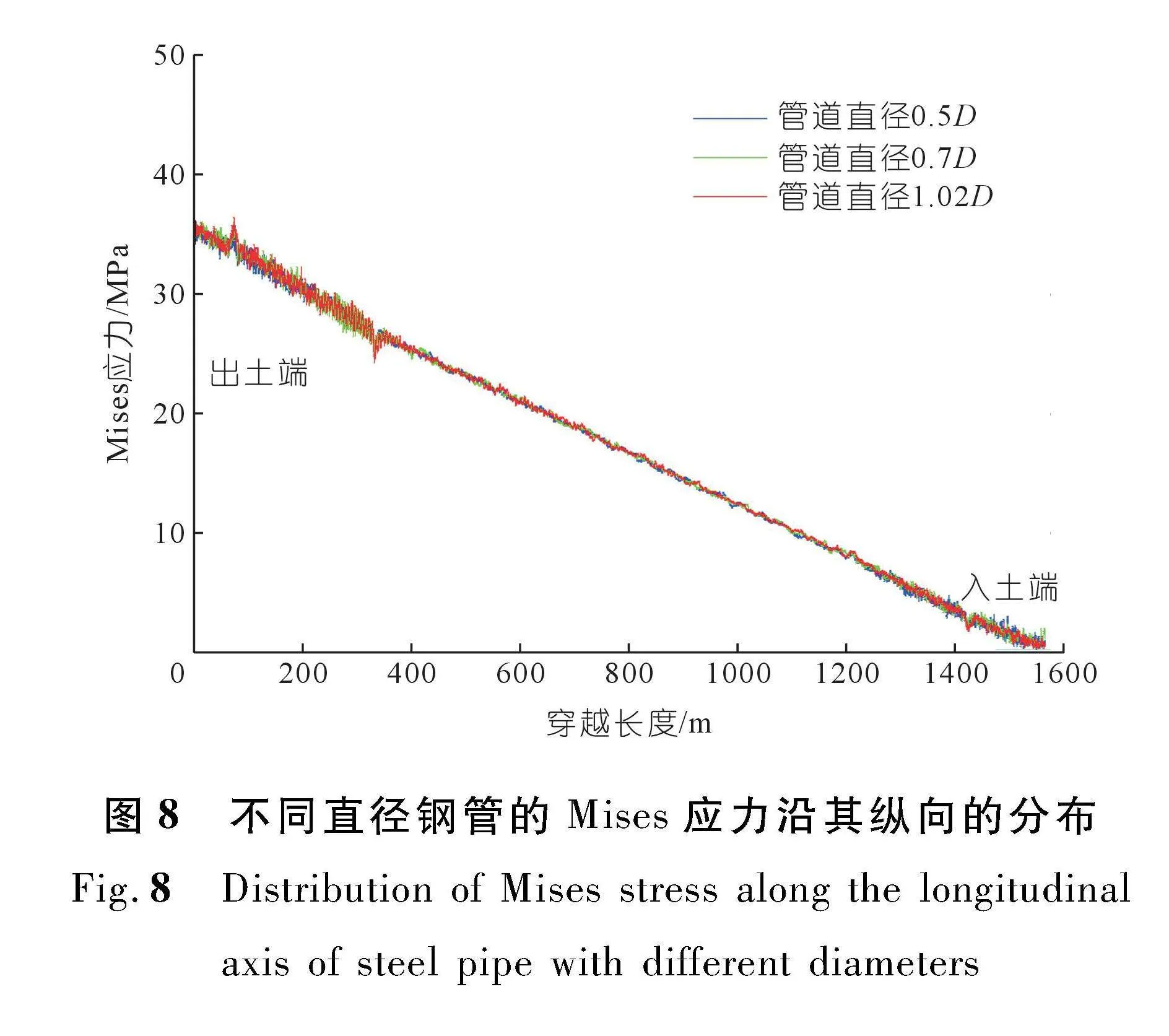
图8为当钢管直径不同时（工况1-1、1-4和1-5）其Mises应力沿管道纵向的分布。从图中可以看出，当管道直径从0.5 m增大到1.02 m，Mises应力并没有显著变化，这说明管道直径对于钢管Mises应力的影响较小。

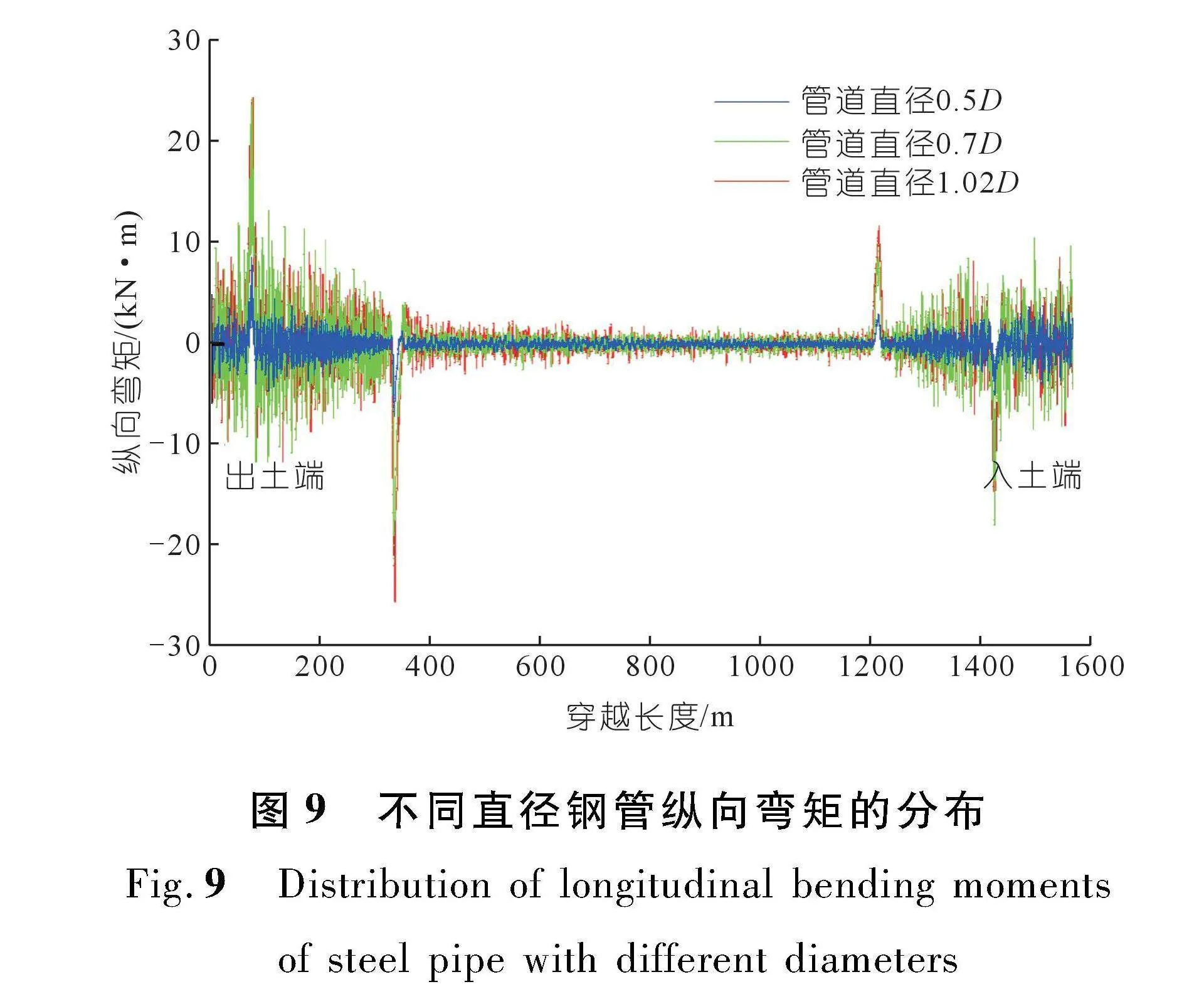
图9为当钢管直径不同时（工况1-1、1-4和1-5）其纵向弯矩的分布。从图中可以看出，在钻孔的弯曲段，钢管的纵向弯矩随着管道直径的增大而增大；而在钻孔的直线段，管道直径对于钢管纵向弯矩的影响较小。此外还可以看出，钢管在出土端的纵向弯矩大于其在入口端的纵向弯矩。

图10为数值模拟工况2-1、2-2和2-3中，不同直径和壁厚的钢管在服役期间发生结构屈曲失稳时的塑性应变分布。从图中可以看出，当钢管发生结构屈曲失稳时，其塑性应变主要集中在顶部、底部及两侧。另外，数值模拟结果表明，当直径为1.02 m、壁厚为26 mm的钢管发生结构屈曲失稳时，其承受的外部压力为7.1 MPa；而当壁厚减小为13 mm时，钢管所能承受的外部压力仅为0.75 MPa。对于直径为0.7 m、壁厚为26 mm的钢管，其发生结构屈曲失稳时所能承受的外部压力则高达25.3 MPa。

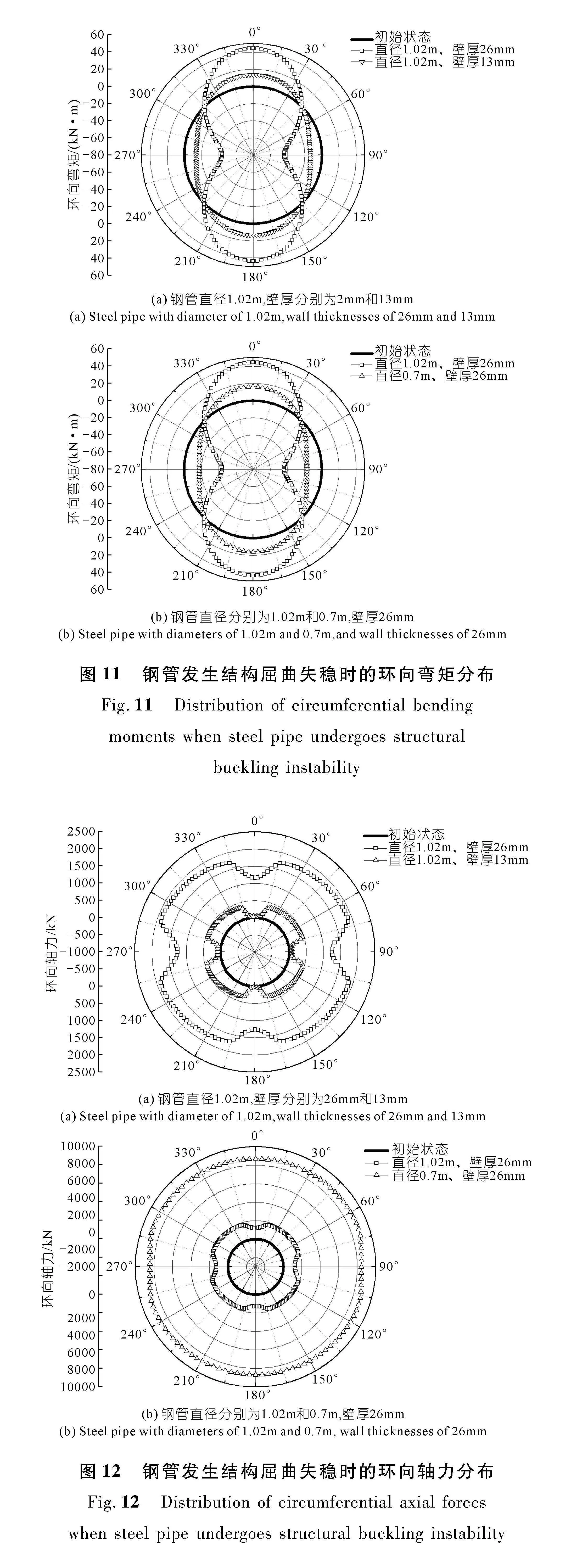
图11为数值模拟工况2-1、2-2和2-3中，钢管在服役期间发生结构屈曲失稳时的环向弯矩分布。需要说明的是，当管道在某一位置外表面受压、内表面受拉时，将作用于该位置处的环向弯矩定义为正；反之，则定义为负。从图中可以看出，管道的环向弯矩绝对值的最大值发生在其顶部、底部和两侧。对于直径1.02 m、壁厚为26 mm和13 mm的钢管，当发生结构屈曲失稳时，其环向弯矩绝对值的最大值分别为44 kN·m和13 kN·m；而对于直径0.7 m、壁厚26 mm的钢管，其环向弯矩绝对值的最大值为16 kN·m。

图12为数值模拟工况2-1、2-2和2-3中，钢管在发生结构屈曲失稳时的环向轴力分布。需要说明

的是，当管道在某一位置环向受压时，将该位置的环向轴力定义为正；反之，则定义为负。从图中可以看出，管道的环向轴力均为正值，这表明管道在静水压力作用下均处于环向受压的状态。从图中还可以看出，当钢管发生结构屈曲失稳时，其环向轴力在管道的顶部、底部和两侧均明显小于其他位置处，与管道发生塑性应变的位置一致（图10）。对于直径1.02 m、壁厚为26 mm和13 mm的钢管，当发生结构屈曲失稳时，其环向轴力最大值分别为1 890 kN和450 kN；而对于直径0.7 m、壁厚26 mm的钢管，其环向轴力最大值为8 630 kN。

6" 结 论

（1） 在回拖过程中，钢管在出土端的Mises应力和纵向弯矩均明显大于入土端。在钻孔的弯曲段，钢管的Mises应力和纵向弯矩均随着弯曲段曲率半径的减小而增大；而在钻孔的直线段，弯曲段曲率半径对于钢管的Mises应力和纵向弯矩的影响均较小。

（2） 在回拖过程中，管道直径的变化对于钢管Mises应力的影响较小。在钻孔的弯曲段，钢管的纵向弯矩随着管道直径的增大而增大；而在钻孔的直线段，管道直径对于钢管纵向弯矩的影响较小。

（3） 当钢管在外部压力作用下发生结构屈曲失稳时，塑性应变主要集中在管道的顶部、底部及其两侧，其所能承受的外部压力随着管道壁厚的增大而增大，随着直径的增大而减小。

（4） 当钢管发生结构屈曲失稳时，其环向弯矩最大值发生在顶部、底部及两侧位置处，并且随着管道壁厚的增大而增大，随着直径的增大而减小；其环向轴力在管道的顶部、底部和两侧均明显小于其他位置，并且随着管道壁厚的增大而增大，随着直径的增大而减小。

参考文献：

［1］" HUEY D P，HAIR J D，MCLEOD K B.Installation loading and stress analysis involved with pipelines installed by horizontal directional drilling［C］∥North American Society for Trenchless Technology，Chicago，1996.

［2］" LAN H T.Experimental and numerical investigation of stability of horizontal boreholes during horizontal directional drilling.Doctoral dissertation［D］.Kingston：Queens′ University，2018.

［3］" 北京市政建设集团有限责任公司.油气输送管道穿越工程施工规范：GB 50424—2015［S］.北京：中国计划出版社，2015.

［4］" 中国石油天然气集团有限公司.给水排水管道工程施工及验收规范：GB 50268—2008［S］.北京：中国建筑工业出版社，2008.

［5］" 郑颖人，邱陈瑜.普氏压力拱理论的局限性［J］.现代隧道技术，2016，53（2）：1-8.

［6］" 郑颖人，朱合华，方正昌，等.地下工程围岩稳定分析与设计理论［M］.北京：人民交通出版社，2012.

［7］" ASTM.Use of maxi-horizontal directional drilling for placement of polyethylene pipe or conduit under obstacles，including river crossings：ASTM F1962—11［S］.West Conshohocken：ASTM，2011.

［8］" American Gas Association.HDD Guidebook［M］.Washington，DC：American Gas Association，1995.

［9］" 陈曦.定向钻回拖过程力学分析［D］.西安：西安石油大学，2015.

［10］王超，胡长明，刘羽，等.水平定向钻扩孔施工地表变形计算分析［J］.人民长江，2023，54（5）：175-181.

［11］蔡亮学，王勐龙，冯宇，等.木楔效应在水平定向钻回拖力预测中的分析与应用［J］.中国石油大学学报（自然科学版），2020，44（5）：139-146.

［12］晁东辉.非开挖水平定向钻孔中的泥浆作用机理研究［D］.上海：上海交通大学，2007.

［13］蔡亮学.水平定向钻管道穿越回拖过程动态力学特性研究［D］.北京：中国石油大学，2011.

［14］郭晓军.HDPE管道在水平定向钻进回拖中的变形损坏机理及数值模拟［D］.成都：成都理工大学，2011.

［15］石贤增，李子涵，康小方.水平定向钻管道回拖影响因素的显著性分析［J］.湖北理工学院学报，2021，37（6）：34-40.

［16］中国石油天然气集团有限公司.油气输送管道工程水平定向钻穿越设计规范：SY/T 6968—2021［S］.北京：石油工业出版社，2021.

［17］艾志久，秦浩，舒建华，等.水平定向穿越扩孔孔形沉降量预测［J］.地下空间与工程学报，2018，14（2）：477-482.

［18］龙江，夏换，周宝库，等.水平定向钻回拖速度对孔壁稳定性的影响［J］.现代隧道技术，2013，50（5）：135-139.

［19］YAN X，WANG X，XIANG W，et al.Buckling behavior of Formed-in-Place-Pipe（FIPP） liners under groundwater pressure：an experimental investigation for buried municipal pipelines［J］.Tunnelling and Underground Space Technology，2023，142：105397.

（编辑：胡旭东）

Mechanical response analysis on pipeline during horizontal directional drilling construction and service period

ZHENG Hua

（Fuzhou Waterworks Engineering Co.，Ltd.，Fuzhou 350025，China）

Abstract：

Multiple factors influence the mechanical response of horizontal directional drilling pipelines during both construction and service period.However，existing theories and calculation methods are notably relied on empirical correction parameters.Based on field measured data，finite element numerical simulation was employed to investigate the stress deformation of steel pipes during the back-pulling process of horizontal directional drilling construction，as well as their structural stability under external pressure.Simulation results revealed that the von Mises stress and longitudinal bending moment at the exit end of the steel pipe were significantly higher compared to those at the entry end during the back-pulling process.Additionally，in the curved section of the borehole，both the von Mises stress and longitudinal bending moment of the steel pipe increased as the curvature radius decreased.In cases of structural buckling instability under external pressure，plastic strain primarily accumulated at the top，bottom and sides of the pipe.Furthermore，the external pressure the pipe can withstand increased with increasing wall thickness and decreased with increasing diameter.

Key words：

horizontal directional drilling； steel pipe； construction pullback； structural stability