基于多目标的易燃易爆品道路运输路径优化

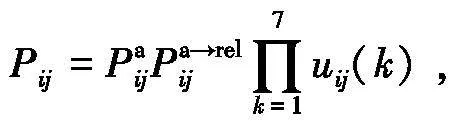
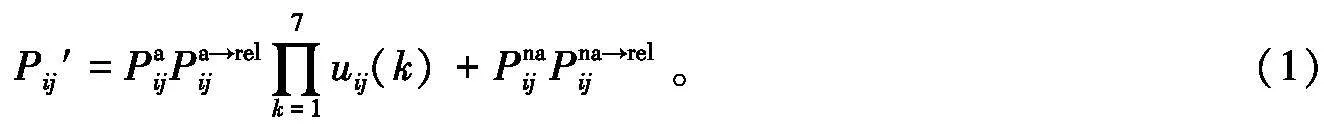
摘要：为提高易燃易爆品道路运输的安全性，考虑道路特征、交通条件及天气状况等对交通事故的影响，确定交通事故影响因素的修正系数，计算因交通事故导致的易燃易爆品泄漏概率，同时考虑因非交通事故导致的易燃易爆品泄漏概率，将二者结合计算易燃易爆品道路运输泄漏事故概率；将道路运输风险细分为人员伤亡风险、环境破坏风险、财产损失风险，量化计算3类风险损失，构建以最小运输风险、运输成本和运输距离为目标的易燃易爆品道路运输路径优化模型。以山东省部分路网为例，采用Dijkstra算法和基于模糊折衷规划的扩展标号法，求解多目标易燃易爆品道路运输路径优化模型。结果表明：计算得到的3条最优路径的运输风险、运输成本、运输距离均较小，相较于最短运输距离路径和最小运输成本路径，优化路径的运输风险大大减小，运输成本和距离略增大。

关键词：易燃易爆品；多目标；路径优化；运输风险

中图分类号：U492.3+36.3文献标志码：A文章编号：1672-0032（2025）01-0009-07

0 引言

我国危险化学品运输量持续增长，危险化学品运输事故率随之增大。2023年我国危险化学品运输总量约为18亿t，因运输成本低、运输距离灵活、运输设施设备完善，道路运输占比超过危险化学品运输总量的60%[1]。易燃类与易爆类化学品运输事故数在所有类别危险化学品道路运输事故数中占比最大，运输过程中一旦发生交通事故，易引发火灾、爆炸等二次事故，造成极大的人员伤亡、环境污染及经济损失[2-3]。为减少易燃易爆品道路运输事故损失，需合理选择易燃易爆品运输车辆的路径。

针对危险化学品道路运输路径选择问题，学者多研究模型构建与求解算法。Pradhananga等[4]针对危险化学品的车辆路径和调度问题，设计双目标决策支持系统，通过元启发式算法求解模型，在满足运输安全的条件下，降低运输成本；Bczkowska[5]以最小运输风险和财产损失为优化目标，提出多目标路径选择模型，基于实际路径数据进行仿真模拟，验证所提方法的可行性；Wang等[6]考虑运输风险、运输成本及路线周围的建筑物和应急设施等因素，建立路径优化模型；Liu等[7]根据运输风险、运输成本和赔偿成本建立路径优化模型，将应急响应时间纳入运输风险评估函数，设计基于线性加权的多目标遗传算法求解模型；Ouertani等[8]考虑客户需求随时间变化的特点，建立以最小运输成本和运输风险为优化目标的模型，通过双群体遗传算法和遗传算法与可变领域搜索相结合的算法求解模型；Zhai等[9]考虑事故概率与速度梯度关系，提出基于爆炸事故风险的路线选择与规划方法。部分学者从多角度构建多目标路径优化模型；任常兴等[10]分析易燃易爆品运输事故的演变模式，提出易燃易爆品道路运输风险指数的计算方法，通过比较运输路线的风险水平选择较优的运输路径；李树民等[11]将运输风险划分为人员风险、财产损失风险与环境损失风险，结合运输成本与运输时间建立多目标路径优化模型；李景娜等[12-13]考虑时间约束和空间尺度，从运输阻抗、运输风险和运输风险敏感度三方面优化运输路径；杨振宏等[14]以运输风险与运输成本为优化目标，优化成品油二次配送的运输路线；刘灿等[15]考虑运输路线的应急保障情况，建立以运输风险、运输成本及运输时间为优化目标的模型，使用遗传模拟退火算法求解模型。优化危险化学品道路运输路径时均考虑运输风险，但缺少对运输风险的细化及量化计算研究，针对易燃易爆品道路运输路径选择的研究也较少，且多忽略非交通事故对运输事故的影响。

本文根据道路实际情况及天气状况，确定交通事故影响因素的修正系数，计算包含因交通事故及非交通事故引起的易燃易爆品道路运输泄漏事故概率；将运输风险分为人员伤亡风险、环境破坏风险及财产损失风险，量化计算三类风险损失，综合考虑运输成本与运输距离，建立多目标易燃易爆品道路运输路径优化模型，采用Dijkstra算法和扩展标号算法求解模型，确定符合决策者风险偏好的易燃易爆品道路运输路径，以期减小易燃易爆品道路运输事故损失。

1 易燃易爆品道路运输泄漏事故概率

运输易燃易爆品的容器破损并泄漏时，易发生爆炸、火灾、中毒等事故，分析易燃易爆品道路运输事故概率主要分析泄漏概率，包括交通事故引起泄漏的概率和非交通事故引起泄漏的概率[16]。

路段ij（i为起点，j为终点）上易燃易爆品运输泄漏事故概率

Pij=PaijPa→relij+PnaijPna→relij，

式中：Paij为路段ij的基本交通事故概率，Pa→relij为路段ij因交通事故导致易燃易爆品泄漏的条件概率，Pnaij为路段ij的基本非交通事故概率，Pna→relij为路段ij因非交通事故导致易燃易爆品泄漏的条件概率。

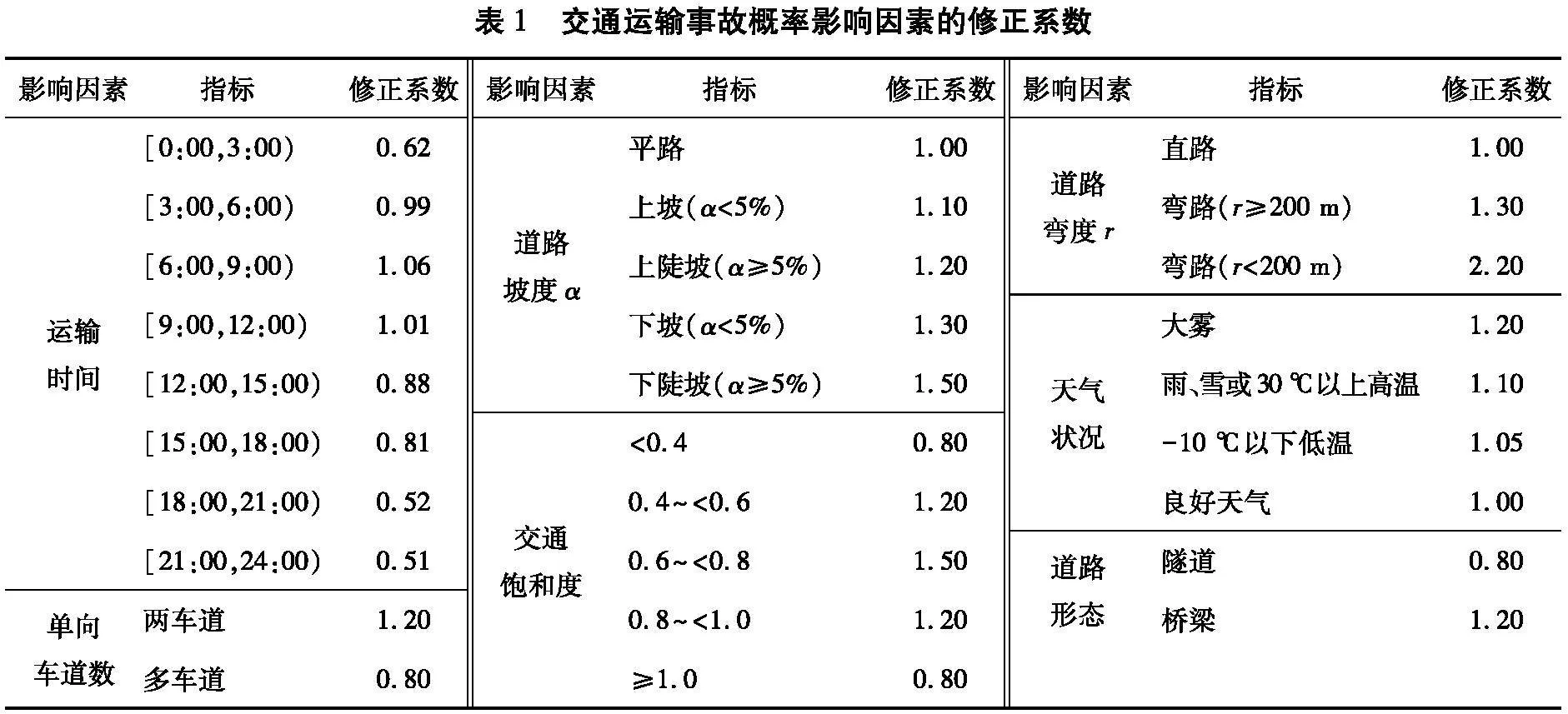
道路特征、交通条件及天气状况等均会对交通运输事故概率产生影响，根据文献[17-18]确定交通事故概率影响因素的修正系数，如表1所示。

综合考虑表1中7类交通事故概率影响因素及其修正系数后，得到因交通事故导致易燃易爆品泄漏的概率

式中uij（k）为路段ij上第k类交通运输事故概率影响因素的修正系数。

经修正后路段ij上易燃易爆品道路运输泄漏事故概率

2 运输路径优化模型建立

2.1 易燃易爆品道路运输泄漏事故影响范围

装有易燃易爆品的运输车辆相当于移动的危险源，计算道路运输泄漏事故影响范围时，采用矩形面积的误差相对较小[19]。路段ij上发生道路运输泄漏事故的影响范围

Sij=2λLij，（2）

式中：λ为最大影响半径，不同种类的危险化学品特性不同，影响半径不同，依据文献[19]取值；Lij为路段ij的长度。

2.2 易燃易爆品道路运输风险

2.2.1 人员伤亡风险

易燃易爆品道路运输泄漏事故造成人员伤亡时，因建筑物的防护作用，室内人员受到的伤害比室外人员小，计算室内、外人员伤亡情况时引入人员暴露概率Pe体现室内外差异[20]。通过人员伤亡补偿成本计算人员伤亡风险损失，路段ij的人员伤亡风险损失

Rpij=SijρijPeNp，（3）

式中：ρij为路段ij两侧人口密度，人/km2；Np为人员伤亡补偿成本，元/人。

2.2.2 环境破坏风险

易燃易爆品道路运输泄漏事故后易发生燃爆事故，燃爆事故对不同类型环境敏感区的影响程度不同。将环境敏感区类型分为风景名胜或自然保护区、农业种植区、水域，其影响权重分别为0.69、0.23、0.08[21]。通过计算环境敏感区的经济损失体现易燃易爆品道路运输事故的环境破坏风险损失，路段ij的环境破坏风险损失

式中：Stij为路段ij上第t类环境敏感区与事故影响区域的叠加面积，m2；εtij为路段ij上第t类环境敏感区的影响权重；Ne为单位面积环境敏感区的影响成本，元/m2。

2.2.3 财产损失风险

道路交通事故财产损失一般包括车辆损失、货物损失和道路及其设施损失，在运输货物与运输车辆一定的情况下，以沿线房屋损毁量作为财产损失评估标准。文献[21]将人均住房面积与影响区内人口数相乘计算事故影响的房屋建筑量，但计算结果与实际差异较大。本文通过软件ArcGIS将事故影响区域房屋建筑区域叠加计算影响房屋面积。引入单位面积房屋修复成本计算财产风险损失，路段ij的财产风险损失

Rhij=ShijNh，（5）

式中：Shij为路段ij的事故影响区域与房屋建筑区域的叠加面积，m2；Nh为单位面积房屋修复成本，元/m2。

易燃易爆品道路运输泄漏事故对道路两侧的人员、环境和财产均造成一定的损失，综合考虑人员伤亡风险、环境破坏风险和财产损失风险得到易燃易爆品道路运输泄漏事故风险损失

Rij=Rpij+Reij+RhijPij′。（6）

2.3 易燃易爆品道路运输成本

运输企业的运输成本主要包括固定成本和可变成本，固定成本包括运输工具成本、设备维护成本等，可变成本包括燃油费、通行费、轮胎费等[22]。本文主要考虑可变成本。

可变成本主要考虑由运输距离和运载量决定的车辆燃油费和高速公路通行费，路段ij的运输成本

Cij=aqLij+ew，（7）

式中：a为易燃易爆品单位运输距离、单位运量的成本，通过调研运输市场获得；q为车辆运输易燃易爆品的质量；ew为高速公路通行费，通过查询高速公路通行费收费标准获得。

2.4 易燃易爆品道路运输路径优化模型

设道路运输网络G=（N，E），N为运输网络中所有节点的集合，E为所有运输路段的集合。以运输风险、运输成本与运输距离最小为目标，建立多目标易燃易爆品道路运输路径优化模型。

目标函数为：

式中：R、C、D分别为易燃易爆品道路运输风险、运输成本、运输距离，xij为决策变量，o为起点，d为终点，mmax为运输车辆最大载质量。

3 应用实例

以山东省部分路网为例，1辆装有20 t 液化石油气的罐车在某日15：00从起点1出发，到目的地11，需选择最优运输路线。分析实际路网后，初步选定路段，路网简化图如图1所示，选定的路段对该车辆无禁限。由图1可知从出发点1到目的地11共有15条可行运输路径。根据当地的交通事故赔偿标准及征地补偿标准等确定人员伤亡成本、环境修复成本与房屋损失成本分别为30 000元/人、20元/m2、200元/m2[23]。

通过软件水经注GIS、百度地图等收集路段长度和路况等信息，通过WorldPop、Zenodo及资源环境科学与数据平台等网站收集人口密度、土地利用及建筑轮廓等数据，采用软件ArcGIS处理收集到的数据，根据式（1）～（7）计算各路段的风险、成本、距离，对计算得到的数据进行最大最小归一化处理，归一化的数据[24]

x′=x－min x/max x－min x，

式中x为原始数据。

各路段的运输风险、运输成本、运输距离归一化数据结果如表2所示，各指标处于同一数量级，适合进行综合评价。

易燃易爆品道路运输最优路径的求解步骤包括6步。

1）采用Dijkstra算法分别求与出发点1相连的有向弧中的最小运输风险、最小运输成本与最小运输距离。

2）分别计算从出发点1到目的地11时运输风险、运输成本、运输距离最小的路径r1、r2、r3，r1为：1→3→6→9→11，r2、r3均为：1→2→7→8→11。

3）分别计算r1、r2、r3的目标值，r1、r2、r3的运输风险分别为0.256 41、1.274 60、1.274 60，运输成本分别为1.578 31、1.133 33、1.133 33，运输距离分别为1.361 97、1.133 33、1.133 33。

4）由步骤3）可得最大运输风险q1=1.274 60，最大运输成本q2=1.578 31，最大运输距离q3=1.361 97。

5）结合步骤1）、4），分别构建运输风险、运输成本、运输距离的隶属度函数1（q1）、2（q2）、3（q3），公式分别为：

6）根据决策者的风险偏好，分配运输风险、运输成本、运输距离的权重分别为0.7、0.2、0.1，选择合适的加权开方-乘方平均算子中的乘方指数α，结合隶属度函数将多目标易燃易爆品道路运输路径优化问题转化为极大化模糊折衷规划问题。

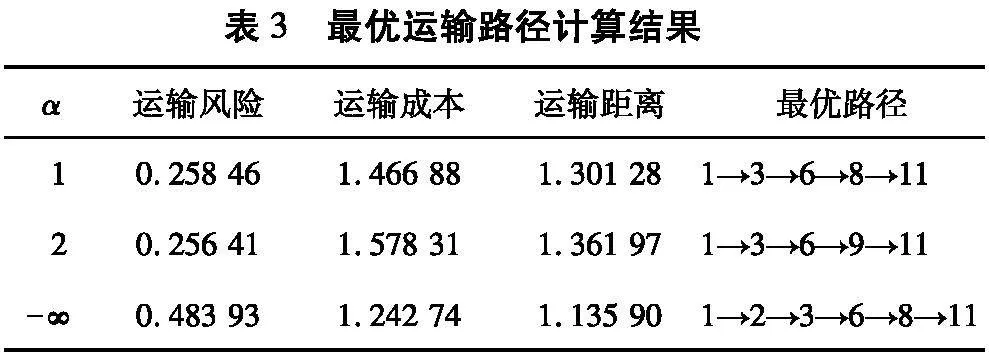
采用基于模糊折衷规划路径选择的扩展标号法[25]计算各路径的模糊折衷值，得到最优运输路径，结果如表3所示。

由表3可知：考虑决策者不同风险偏好条件下计算得最优运输路径依次为1→3→6→8→11、1→3→6→9→11、1→2→3→6→8→11。最小运输距离、运输成本路径均为1→2→7→8→11，该路径对应的运输风险、运输成本、运输距离分别为1.274 60，1.133 33、1.133 33，最小运输成本与最小运输距离的路径的运输风险远大于计算得到的最优路径。若选择最短运输距离路线时，因该路径两侧的人口、房屋与环境敏感区密度较大，发生运输泄漏事故时易造成较大的人员、环境和财产损失。

4 结束语

考虑非交通事故与交通事故对易燃易爆品道路运输泄漏事故概率的影响，根据道路特征、交通条件及天气状况等修正运输事故概率的影响因素，能较准确地计算在一定路径上发生易燃易爆品道路运输事故的概率。量化计算易燃易爆品道路运输泄漏事故造成的人员伤亡损失、环境损失及财产损失，以最小运输风险、运输成本及运输距离为目标建立易燃易爆品道路运输路径优化模型。以真实路网为例，验证建立的易燃易爆品道路运输路径优化模型的有效性，通过基于模糊折衷规划的扩展标号法求解得到3条最优运输路径，运输成本略增，但运输风险大大减小。

参考文献：

[1] 中国物流与采购联合会危化品物流分会. 刘宇航：2023中国化工物流行业发展运行报告[R/OL].（2023-12-06） [2024-04-15].http：//whpwlfh.chinawuliu.com.cn/gzdt/202312/06/622354.shtml.

[2] 曹建，施式亮，鲁义，等.2013—2018年罐车公路运输危化品事故分析[J].中国安全科学学报，2020，30（2）：119-126.

[3] 王建豪，曹瑞祥，宁泽辉，等.重特大危险化学品道路运输事故原因与预防[J].山东交通学院学报，2021，29（3）：17-24.

[4] PRADHANANGA R， TANIGUCHI E， YAMADA T， et al. Bi-objective decision support system for routing and scheduling of hazardous materials[J].Socio-Economic Planning Sciences， 2014，48（2）：135-148.

[5] BCZKOWSKA S. The method of optimal route selection in road transport of dangerous goods[J].Transportation Research Procedia， 2019，40：1252-1259.

[6] WANG Y， ROR N， ZHANG B. Multi-objective transportation route optimization for hazardous materials based on GIS[J].Journal of Loss Prevention in the Process Industries， 2023：104954.

[7] LIU L P， LI J M， ZHOU L， et al. Research on route optimization of hazardous materials transportation considering risk equity[J].Sustainability， 2021，13（16）：9427.

[8] OUERTANI N， BEN-ROMDHANE H， KRICHEN S. A decision support system for the dynamic hazardous materials vehicle routing problem[J].Operational Research， 2022，22：551-576.

[9] ZHAI C L， LI P L， ZHAO R H， et al. Selection and planning of hazardous materials transportation routes based on explosion accident risks[J].Journal of Loss Prevention in the Process Industries， 2024，92：105440.

[10] 任常兴，王婕，吕东，等.易燃易爆危险品道路运输风险指数评价法[J].工业安全与环保，2012，38（8）：17-19.

[11] 李树民，刘勇杰.危险品道路运输多目标路线优化研究[J].物流科技，2019，42（10）：118-121.

[12] 李景娜，王静虹，潘旭海.带时间窗约束的危险化学品运输路径优化[J].南京工业大学学报（自然科学版），2019，41（5）：586-592.

[13] 李景娜，王静虹，潘旭海，等.不同空间尺度下危化品运输路径优化[J].中国安全生产科学技术，2018，14（8）：152-157.

[14] 杨振宏，刘欢，白雪，等.考虑风险的成品油道路运输路径优化[J].安全与环境学报，2022，22（2）：926-932.

[15] 刘灿，周荣义，石云霄，等.考虑应急保障的危化品道路运输多目标路径优化方法[J].矿业工程研究，2024，39（2）：49-54.

[16] 李树民.基于风险分析的危化品道路运输路线选择研究[D].长沙：长沙理工大学，2020.

[17] 沈小燕.道路危险货物运输风险分析及路线优化研究[D].西安：长安大学，2009.

[18] 任常兴.基于风险分析的危险品道路运输路径优化方法研究[D].天津：南开大学，2007.

[19] 周晶燕.基于风险分析的危险品道路运输多目标优化研究[D].武汉：武汉理工大学，2020.

[20] 任竞舟.道路危险化学品运输风险评估模型及选线优化研究[D].湘潭：湖南科技大学，2016.

[21] 曾琳惠.易燃易爆品道路运输路线选择问题研究[D].成都：西南交通大学，2011.

[22] 朱理想，刘军，葛鹏，等.航道与公路货物运输成本定量对比分析：以深圳至广州货物运输为例[J].湖南交通科技，2023，49（3）：176-180.

[23] 华律网.山东省交通事故赔偿标准[EB/OL].（2024-09-06）[2024-09-25].https：//www.66law.cn/laws/1839735.aspx.

[24] 杨寒雨，赵晓永，王磊.数据归一化方法综述[J].计算机工程与应用，2023，59（3）：13-22.

[25] 帅斌，种鹏云.基于决策者风险偏好的危险货物运输路径优化问题研究[J].铁道货运，2011，29（1）：9-13.

Multi-objective path optimization for the road transportation of

flammable and explosive materials

Abstract：In order to improve the safety of road transportation of flammable and explosive materials， considering the impact of road characteristics， traffic conditions， and weather conditions on traffic accidents， the correction coefficient of traffic accident influencing factors is determined， and the probability of flammable and explosive material leakage caused by traffic accidents is calculated. At the same time， the probability of flammable and explosive material leakage caused by non-traffic accidents is considered， and the probability of flammable and explosive material road transportation leakage accidents is obtained by combining the two.The road transportation risk is subdivided into personnel injury risk， environmental damage risk， and property loss risk， and the three types of risk losses are quantitatively calculated to construct a flammable and explosive material road transportation path optimization model with the goal of minimum transportation risk， transportation cost， and transportation distance. Taking some road networks in Shandong Province as an example， the Dijkstra algorithm and the extended labeling method based on fuzzy compromise programming are used to solve the multi-objective road transportation path optimization model for flammable and explosive materials. The results show that the transportation risk， transportation cost， and transportation distance of the three optimal routes calculated are small. Compared with the shortest transportation distance route and the minimum transportation cost route， the transportation risk of the optimized route is greatly reduced， and the transportation cost and distance are slightly increased.

Keywords：flammable and explosive materials；multi-objective；path optimization；transportation risk