交通锥收放装置设计及关键部件优化

摘要：为解决交通锥收放装置存在收放不稳定、通用性较差、施放效率较低等问题，提出一种新型交通锥收放装置设计及关键部件优化方案，采用有限元分析软件ANSYS Workbench对交通锥收放装置中质量占比最大的一体式框架进行优化设计。在极限工况下对一体式框架进行静力学分析，基于最优空间填充设计方法进行试验设计，采用基因聚合法进行响应面拟合，得出设计点、拟合优度和相关灵敏度图，获取结构尺寸参数对几何质量、总变形、等效应力的影响关系。采用多目标遗传算法NSGA-II寻优，获得最佳优化方案。结果表明：与原模型相比，优化模型质量减少30.6%，且满足材料屈服强度和结构刚度设计要求。

关键词：交通锥收放装置；一体式框架；静力学分析；响应面拟合；多目标遗传算法NSGA-II

中图分类号：U417;TH69文献标志码：A文章编号：1672-0032（2025）01-0082-08

0 引言

交通锥是由塑料或橡胶制成的空心锥体，常用作公路封闭、应急施工、车道隔离分流等标志[1]。根据2022年交通运输部发布的《国家公路网规划》，到2035年，国家公路网总规模达4.61×105 km[2]。传统公路养护一般采取人工收放交通锥的方式，费时费力，劳动强度大，工作环境危险。采用交通锥收放装置代替人工作业，对提高公路养护工作效率、降低公路养护工人发生交通安全事故概率具有重要意义[3-4]。

国内外诸多学者对交通锥收放装置进行大量研究。张秀维[5]设计NL-100型交通路锥自动收放车，建立回收机构有限元模型，通过静力学分析、动态特性分析验证回收机构的材料强度、结构刚度及可靠性。陈元瑗[6]设计一种交通锥收放机，采用动力学仿真软件ADAMS分析各部件间的运动关系，为结构优化与产品试制提供技术支持。楚恒[7]设计一种交通锥自动收放装置，开展动力学及运动学分析和仿真研究，实现交通锥内部子系统独立运动和协调运动，缩短交通锥收放时间。崔龙飞等[8]采用有限元分析软件ABAQUS对某路锥收放车回转升降机构进行静力学分析，根据分析结果修改结构材料和局部模型，修改后结构的最大应力和最大位移减小。Orthaus等[9]设计一种交通锥半自动布放装置，布锥方式由人工手动将交通锥单独放到弧形滑道上端，在控制系统管控下按预期时间或距离在重力作用下自由滑落到地面，收锥时需人工操作。Hargadon[10]研制车载交通锥收放机AutoCone 500，存储装置外形为圆鼓状，可容纳500个交通锥；拾取装置为机械臂，摆放交通锥时抓取交通锥上端将其置于路面，回收时与摆放动作相反，1个交通锥的收放周期约为10 s。已有研究主要侧重于交通锥收放装置的设计，对交通锥收放装置结构的尺寸优化研究较少；已有交通锥收放装置仅能收放单一尺寸的交通锥，在收放过程中存在掉锥现象。

本文以交通锥收放装置为研究对象，提出一种新型交通锥收放装置设计方案，将质量占比大的一体式框架作为优化对象，通过响应面优化方法和多目标遗传算法NSGA-II对其进行轻量化设计，对优化后的一体式框架进行静力学分析，以期为交通锥收放装置结构优化升级提供指导。

1 交通锥收放装置设计方案

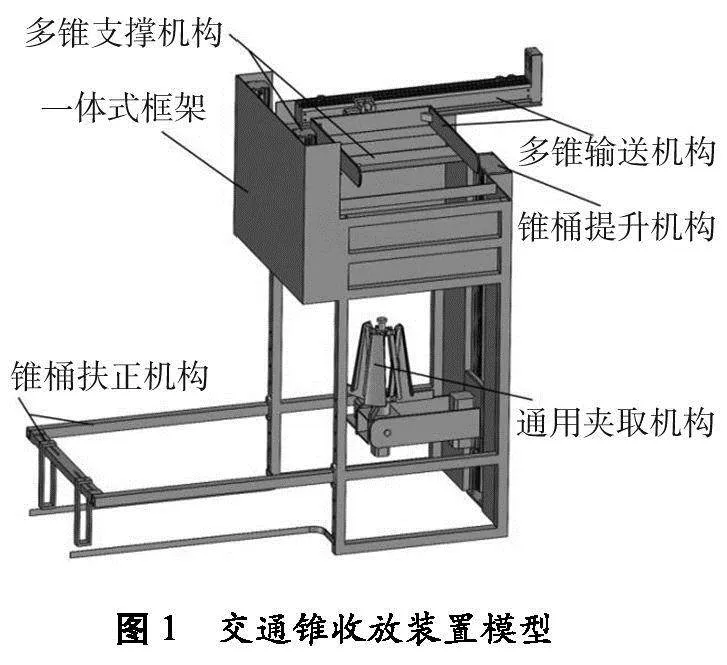
交通锥收放装置主要由一体式框架、通用夹取机构、锥桶扶正机构、锥桶提升机构、多锥支撑机构和多锥输送机构组成，如图1所示。一体式框架左右两侧由方形钢管焊接而成，背部焊接一块钢板固定各机构。锥桶扶正机构可根据收放交通锥的尺寸调节移动滑块的宽度和高度，满足不同尺寸交通锥的扶正与放倒。通用夹取机构可夹紧和放松不同尺寸交通锥，通过锥桶提升机构实现升降动作。多锥支撑机构主要收取和支撑通用夹取机构上的交通锥，使收取的交通锥保持在原位置，并等待下一个交通锥的到来。收取10个交通锥后，将交通锥提升到一定高度，由多维输送机构通过移动框架推动交通锥到达皮带机或其他交通锥存储装置进行存储，再将交通锥移动框架逆时针旋转90°，回到初始位置等待下次输送工作；放置交通锥时，多锥支撑机构和多锥输送机构动作与收取相反。

2 一体式框架有限元分析

一体式框架整体结构简单且规则。选用普通碳钢制作一体式框架，密度为7 850 kg/m3，弹性模量为200 GPa，泊松比为0.3，屈服强度为250 MPa。

采用ANSYS Workbench切片功能（slice）处理一体式框架，采用多区域划分网格方法，控制单元边长为8 mm，共划分为695 410个网格节点，273 171个单元。由ANSYS Workbench中网格单元划分信息处理结果可知，网格单元质量为0.76，质量较高，能确保有限元分析结果具有较高的可信度[11]。

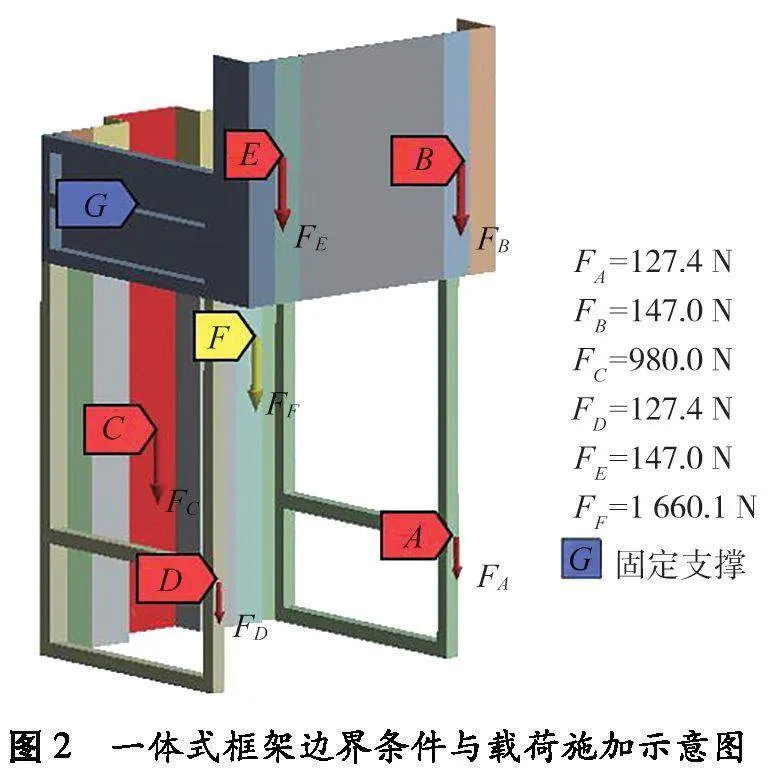
将一体式框架背部凹型板与车体的连接视为固定约束。凹型板与锥桶提升机构形成矩形接触面C，接触面C处相关机构、10个交通锥及其他零件总质量约为100.0 kg，对此处施加垂直向下的载荷980.0 N。一体式框架前端与2组多锥支撑机构形成2个矩形接触面B和E，多锥支撑机构总质量约为30.0 kg，对接触面B和F处分别施加垂直向下的载荷147.0 N。锥桶扶正机构通过螺栓连接一体式框架，形成圆形接触面A和D，锥桶扶正机构总质量约为26.0 kg，对接触面A、D分别施加垂直向下的载荷127.4 N。一体式框架总质量约为169.4 kg，对一体式框架添加垂直向下的自身重力1 661.1 N。一体式框架边界条件与载荷施加示意图如图2所示。

通过ANSYS Workbench求得一体式框架总变形和等效应力云图，如图3所示。

由图3可知：1）一体式框架最大变形约为4.1 mm，发生在矩形框架上端处，一体式框架的背部凹型板处与车体为固定约束，变形相对较小。矩形框架主要受多锥支撑机构的重力，矩形框架下端连接一体式框架，上端与交通锥收放装置中其他结构无连接，矩形框架下端变形大于一体式框架，小于矩形框架上端。一体式框架整体变形范围为0.001～4.100 mm，对收放装置的收放精度影响较小。2）等效应力主要分布在一体式框架背部，最大等效应力位于固定支撑G处，为69.102 MPa，主要受应力集中影响，固定支撑G处实际应力往往小于仿真结果。一体式框架整体应力为0.003～69.102 MPa，所选钢材的屈服强度σS=250 MPa，取安全系数nS=2，则许用应力σ=125 MPa，一体式框架整体范围的应力均小于许用应力，满足选用的普通碳钢材料强度要求[5]。

3 一体式框架响应面优化

3.1 响应面模型的建立

响应面优化是一种用于优化多变量系统设计的统计建模方法，通过构建数学模型预测响应变量（或目标函数）与设计变量间关系，寻找最佳设计参数组合，达到最优目标[12-13]。

进行优化设计时，可通过响应面法得到未知响应与设计变量二者间的真实函数关系[14]。一体式框架有多个变量且两两间为非线性关系，通过二次多项式建立拟合函数：

式中：y为试验输出量，xi、xj为设计变量，β0、βi、βii、βij为系数，ε为观测误差。

3.2 设定设计变量及试验方法

进行试验设计前，需对一体式框架进行参数化处理，设计变量分自变量和因变量。自变量为：框架背板厚度P1、矩形背板厚度P2、固定模组板厚度P3、横支撑方形钢管厚度P4、纵支撑方形钢管厚度P5；因变量为：几何质量P6、总变形P7、等效应力P8。设计变量初始值及变化范围如表1所示。

设计变量分配完成后，试验类型选用最优空间填充设计，通过最少的试验点最大化地覆盖整个设计空间，分布更均匀，确保试验结果能全面、准确地反映系统或模型。通过中心复合设计采样类型，生成27组试验样本点数据，如表2所示。

3.3 响应曲面拟合及分析

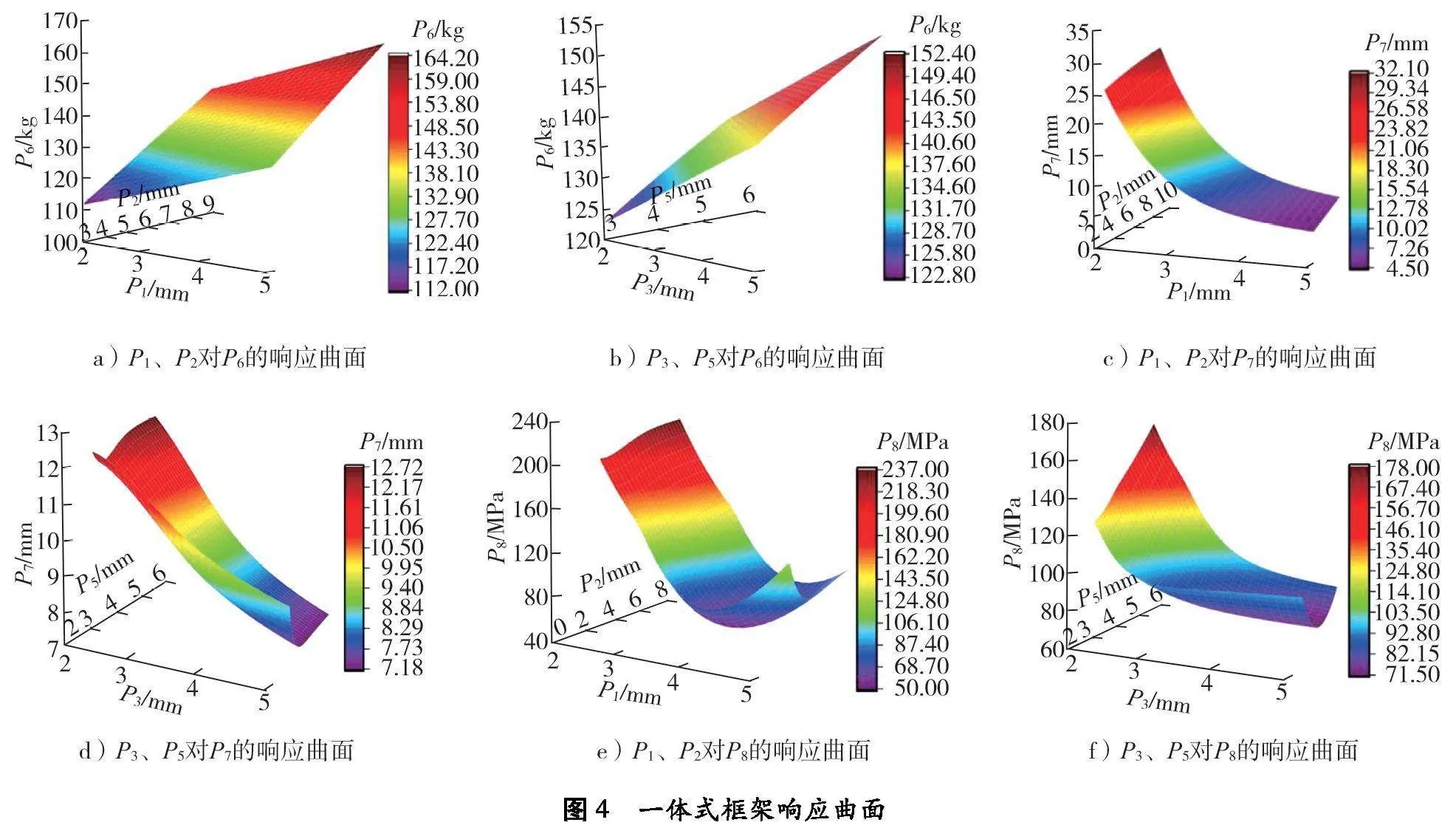
采用基因聚合法分析自变量对因变量的影响，并拟合生成响应曲面，拟合结果如图4所示。基因聚合法根据全二阶多项式、非参数回归、克里格法和最小二乘法等不同元模型的加权平均，结合各约束条件，选择最适合输出参数的响应曲面类型，并多次求解和交叉验证，最终输出拟合响应曲面[15]。

由图4可知：一体式框架几何质量与厚度呈线性关系，并随厚度参数P1、P2、P3、P5的增大而增大。一体式框架总变形与厚度呈非线性关系，随参数P1、P3的增大，总变形减小；参数P2和P5对总变形影响较小。一体式框架等效应力与厚度呈非线性关系，随参数P1的增大，等效应力先减小后增大；随参数P3增大，等效应力减小；随参数P2和P5的增大，等效应力增大。

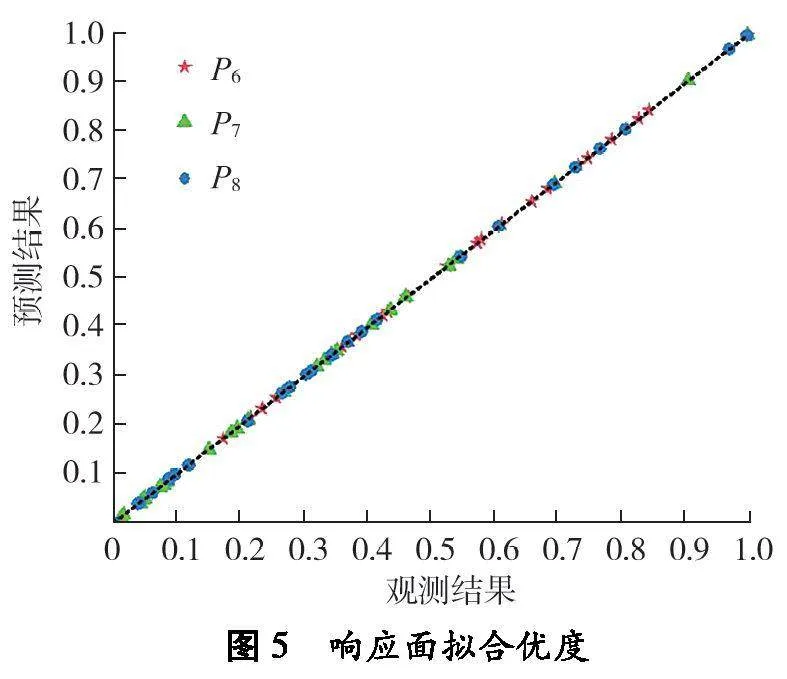
通过在响应曲面中设置验证点并计算拟合优度评估响应面的精确程度[16]，响应面拟合优度如图5所示。拟合优度是指回归直线对观测结果的拟合程度。采用决定系数R2度量拟合优度的统计量，最大值为1，R2越接近1，说明回归直线对观测结果的拟合程度越好，反之，拟合程度越差。本文中设计变量（厚度参数P1～P5）共5个，因设计变量的数量较多致使残差平方和减小，导致R2增大，影响判断拟合优度。需引入修正决定系数Rz2，避免设计变量数量过多对R2产生影响。决定系数R2和修正决定系数Rz2如表3所示。由图5和表3可知：预测结果与设计点观测结果拟合程度较高，即拟合优度较好。

对厚度参数进行局部灵敏度分析，结果如表4所示。局部灵敏度分析是计算系统模型的输出变量或状态对系统参数和周围条件变化敏感程度的一种方法[17]。分析不同参数对系统模型的影响程度，找出主要影响因素，为优化系统参数、提高优化目标提供依据[18]。

由表4可知：P1、P2、P3、P5与P6正相关，P1、P2、P3、P5与P6的灵敏度分析结果与响应曲面拟合结果均一致，P2、P1、P3、P5对P6的影响依次减小；P4与P6负相关，影响程度较小;P1、P3、P5与P7负相关，P2、P4与P7正相关;P1、P3与P8负相关，P2、P4、P5与P8正相关;P1对P7和P8的影响程度最大，P3次之，其他厚度参数影响相对较小。

3.4 建模及寻优结果分析

3.4.1 构建数学模型

采用响应曲面优化（response surface optimization，RSO）方法对一体式框架响应曲面模型其进行尺寸优化求解。RSO优化设计的数学模型为：

式中：min f（x）、min M（x）为等效应力、几何质量的最小目标函数；xi为第i个设计变量参数，xmini、xmaxi分别为第i个设计变量参数的上限、下限，mm；θ为总变形，mm；m为一体式框架质量，kg。

3.4.2 寻优结果分析

采用多目标遗传算法NSGA-II，根据式（1）计算并寻找全局最优解，多目标遗传算法NSGA-II是基于受控精英主义概念的流行非支配排序遗传算法的变体，由Srinivas和Deb于1995年提出，该算法在基本遗传算法的基础上改进，在多目标优化、寻找全局最优解领域应用广泛[19]。根据P6、P7和P8在满足所有约束条件下优化设计问题的可行点，形成权衡图，如图6所示。权衡图反映可视化设计参数与优化目标间的关系，在设计过程中工程人员根据权衡图平衡不同参数间的影响，找到最优设计参数组合[20]。

由图6可知：该优化设计问题存在多组处于理想范围的可行点。

采用多目标遗传算法NSGA-II，以最初生成5 000个可行点样本为基础，每次迭代1 000个可行点样本，在20次迭代中求得3组候选样本作为该优化设计问题的最满意解，一体式框架优化尺寸候选点数据如表5所示。

计算候选点1，可得一体式框架的质量为108.48 kg，等效应力为37.747 MPa，总变形为7.886 mm；计算候选点2，一体式框架质量为108.02 kg，等效应力为38.533 MPa，总变形为7.876 mm；计算候选点3，一体式框架质量为107.65 kg，等效应力为39.369 MPa，总变形为8.055 mm。3组候选点各参数变化范围较小，比原尺寸变化较大，综合考虑3组候选点计算所得的一体式框架质量、等效应力和总变形，选择候选点1为最终优化方案。一体式框架由方形钢管焊接而成，方形钢管属于特定型材，截面尺寸大多为整数，只在特殊情况下，部分尺寸可精确到小数点后1位，但必须是0或5[21]。候选点1的厚度为非规则数值，与实际生产要求不符，须对参数进行圆整处理，圆整后P1～P5分别为4.0、3.5、2.0、5.5、3.0 mm。

4 优化结果验证

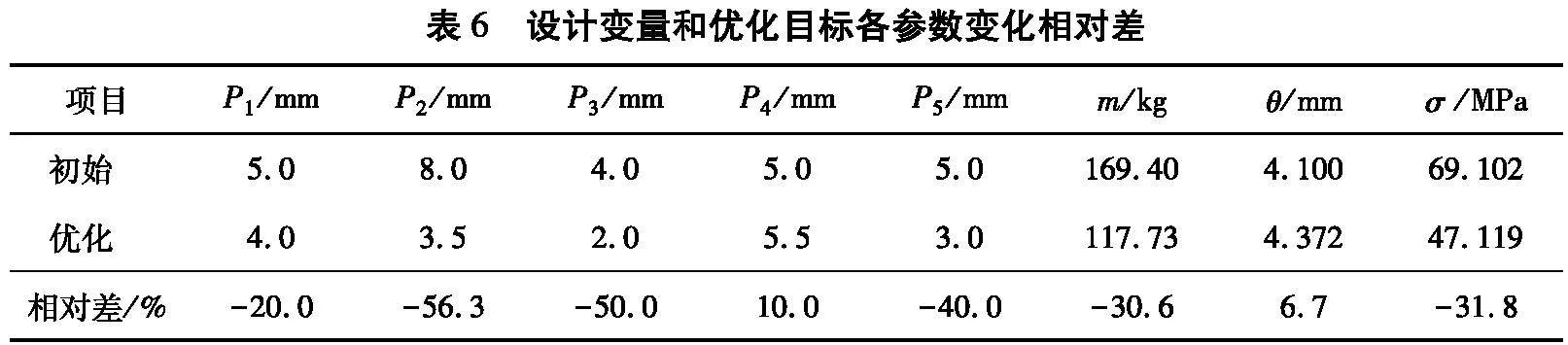
将优化后的参数代入一体式框架进行静力学分析，设定材料、网格大小、边界条件、受力大小以及施加方式，各设定参数与前文保持一致，设计变量和优化目标各参数变化相对差如表6所示，优化后一体式框架总变形和等效应力云图如图7所示。

由表6可知：P2、P3、P5的初始值与优化结果的相对差较大，P1、P4的初始值与优化结果的相对差较小。设计前期过度考虑一体式框架受力、变形、收放精度等综合因素，P2、P3、P5设置不合理，导致三者的初始值与优化结果相对差较大，但可通过响应面优化设计改进。

采用响应面优化方法和多目标遗传算法NSGA-II，以几何质量和等效应力为优化目标对一体式框架进行优化设计，使其质量减小30.6%，达到轻量化设计目的。一体式框架材料屈服强度和结构刚度均在合理范围内[22]，总变形由4.100 mm增至4.372 mm，增大6.7%；等效应力由69.102 MPa降至47.119 MPa，减小31.8%。

5 结论

1）通过对交通锥收放装置的结构和功能分析，提出一种通用性强、可靠性高的轻量化交通锥收放装置设计方案，可大幅度节省人力资源。

2）采用ANSYS Workbench对一体式框架模型进行静力学分析，获得一体式框架总变形云图和等效应力云图，验证一体式框架材料屈服强度和结构刚度均满足要求。

3）以一体式框架轻量化设计为目标，以变形和许用应力为约束条件，以一体式框架各部分厚度为待优化参数，通过基因聚合法建立设计变量与优化目标参数间的拟合响应曲面，应用多目标遗传算法NSGA-II，寻求全局最优解。将最优解代入三维模型，经评估，一体式框架质量减小30.6%。对优化后的一体式框架进行静力学分析验证，结果表明，一体式框架材料屈服强度和结构刚度均符合要求。

参考文献：

[1] ZENG J W， QIAN Y S， WANG B B， et al. The impact of traffic crashes on urban network traffic flow[J].Sustainability， 2019， 11（14）：3956.

[2] 中华人民共和国交通运输部.国家发展改革委 交通交通运输部关于印发《国家公路网规划》的通知[EB/OL].（2022-07-04）[2024-06-12].https：//xxgk.mot.gov.cn/2020/jigou/zhghs/202207/t20220711_3660995.html.

[3] 刘锦翼，夏冉，李国铭.交通锥自动收放装备设计与应用研究[J].人民交通，2019（12）：79-80.

[4] 吴泽东，王明武，韩继科，等.小型交通锥筒自动收放机设计与研究[J].陕西理工大学学报（自然科学版），2023，39（6）：24-31.

[5] 张秀维.交通路锥自动收放系统的设计与研究[D].南京：南京理工大学，2013.

[6] 陈元瑗.交通锥自动收放机设计与研究[D].西安：长安大学，2013.

[7] 楚恒.交通锥收放车自动收放装置研究[D].西安：长安大学，2022.

[8] 崔龙飞，张龙，马大为，等.某路锥收放车回转升降机构有限元分析与结构优化[J].机床与液压，2014，42（3）：142-147.

[9] ORTHAUS C， ANDERSON M， ZIMMERMAN J， et al. Traffic cone setting devices for depositing traffic cones onto roadway surfaces： U.S. Patent 6726434[P].2004-03-25.

[10] HARGADON A. Automated cone machine[D].USA，Davis： UC Davis， 2013.

[11] 沈仙法，刘浩，陈晓颖.多功能可分离助老床椅的结构设计与有限元分析[J].机械设计，2023，40（10）：114-121.

[12] 张鹏程，张洪丽，赵金洋.基于Workbench的某轨道机器人主体关键零部件的轻量化设计[J].机械工程师，2023（12）：135-139.

[13] 刘光辉，殷鸣，尹湘云，等.基于响应面的码垛机器人承载体多目标优化[J].机械，2020，47（6）：56-61.

[14] 徐新，邓斌，刘宁波.一种艾灸装置的结构设计及支撑座的优化设计[J].机械设计与制造，2024（2）：332-337.

[15] ALPASLAN E， HACIEFENDIOGLU K， DEMIR G， et al. Response surface-based finite-element model updating of a historic masonry minaret for operational modal analysis[J].The Structural Design of Tall and Special Buildings， 2020：e1773.

[16] 陈寰宇，宇文璋杰，寇元超，等.基于ANSYS的振动转接夹具多目标优化设计[J].科技与创新，2024（12）：37-39.

[17] CHEN Z W， LI C， HAN X， et al. Sensitivity analysis of the MIG welding process parameters based on response surface method[J].Journal of Adhesion Science and Technology，2021，35（6）：590-609.

[18] 欧栋，王建梅，宁可，等.基于响应面分析的风力发电机主轴优化设计[J].机械设计，2024，41（4）：110-116.

[19] 刘高照，管殿柱，施磊，等.锻造专用机械臂的结构有限元分析及优化设计[J].锻压技术，2024，49（5）：160-165.

[20] 孙永国，金欣，薛冬，等.基于NSGA-Ⅱ的滑油泵叶轮结构优化设计[J].中国机械工程，2024，35（3）：559-569.

[21] 邢伟.某型号直臂式高空作业平台臂架结构分析及优化[D].秦皇岛：燕山大学，2020.

[22] 孙凯.基于响应面法的液压机械臂结构优化[J].起重运输机械，2023（22）：41-46.

Design of traffic cone retractable device and optimization of

key components

Abstract：To address the issues of unstable deployment and retrieval， poor versatility， and low deployment"efficiency in traffic cone retractable device， a new design of traffic cone retractable device and optimization of key components are proposed. The finite element analysis software ANSYS Workbench" is used to optimize the design of the integrated framework， which accounts for the largest proportion of mass in the traffic cone retractable device. Static analysis is performed on the integrated framework under extreme working conditions. Based on the optimal space-filling design method， the experimental design is carried out， and the response surface fitting is carried out by genetic aggregation method. The design point， goodness of fit and related sensitivity diagram are obtained， and the influence of structural size parameters on geometric quality， total deformation and equivalent stress is revealed. The multi-objective genetic algorithm NSGA-II is employed for optimization to obtain the best optimization scheme. The results show that compared with the original model， the optimized model reduces mass by 30.6% while meeting the requirements for material yield strength and structural stiffness design.

Keywords：traffic cone retractable device; integrated framework; static analysis; response surface fitting; multi-objective genetic algorithm NSGA-II