浅析样本估计总体的“四个方向”

利用统计知识来进行数据收集、分析与处理时，经常要通过合理的数据处理，借助样本来估计总体，为保证数据分析过程的科学性，往往需要从总体取值规律、总体百分位数、总体集中趋势及总体离散程度四个方向的估计来实现，达到统计分析与应用的科学性与有效性。

一、总体取值规律的估计

总体取值规律的估计，主要以频率分布、频率分布直方图等形式来设置，从中看出数据取值规律及其分布特点。

例1某企业招聘，一共有200名应聘者参加笔试，他们的笔试成绩都在[40，100]内，按照[40，50），[50，60），…，[90，100]分组，得到如图1所示的频率分布直方图，则a=______;该企业根据笔试成绩从高到低进行录取，若计划录取150人，估计应该把录取的分数线定为______分。

解析：依题意，由（0.005+0.010+a+0.030+a+0.015）×10=1，解得a=0.020。因为150/200=0.75，所以1-0.75=0.25。又因为（0.005+0.010）×10=0.15，（0.005+0.010+0.020）×10=0.35，所以录取的分数线应定在[60，70）内。设分数线定为m分，则0.15+（m-60）×0.020=0.25，解得m=65，所以应该把录取的分数线定为65分。故填0.020;65。

点评：熟悉频率分布直方图的结构特征及数据特点，方便从中确定一些相关的数据信息，如图中纵轴上的数据是各组的频率除以组距的结果，图中各小长方形的面积之和为1等，这些都是识图与用图的关键。

二、总体百分位数的估计

总体百分位数的估计，主要以第几个百分位数的确定与应用等形式来设置，借助数据分析与数学运算来求解。

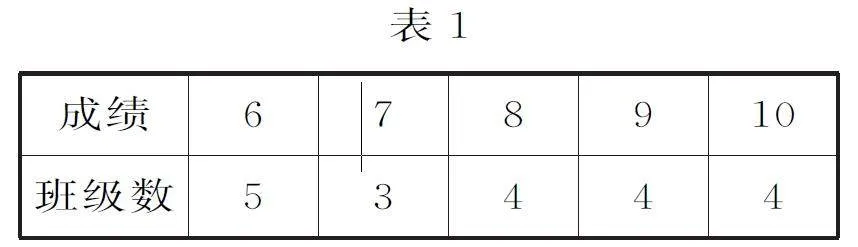
例2（1）某校举行了全校大课间跑操比赛。现从该校随机抽取20个班级的比赛成绩，得到如表1所示的统计表，由统计表可得这20个比赛成绩的第80百分位数是（）。

A.8.5B.9C.9.5D.10

（2）已知一组数据1.3，2.1，2.6，3.7，5.5，7.9，x，9.9的第65百分位数是7.9，则实数x的取值范围是（）。

A.[7.9，+∞）B.（7.9，+∞）

C.[7.9，9.9]D.（7.9，9.9）

解析：（1）依题意，由20×80%=16可知第80百分位数是第16个和第17个成绩的平均数。由题表数据可知第16个成绩为9，第17个成绩为10，所以第80百分位数为9+10/2=9.5。故选C。

（2）因为8×0.65=5.2，所以第65百分位数是第6个数，将除去x的其他数据从小到大排序可得1.3，2.1，2.6，3.7，5.5，7.9，9.9。当xlt;7.9时，则第6个数可能是x或5.5，不符合题意;当x≥7.9时，则第6个数是7.9，符合题意。综上所述，实数x的取值范围是[7.9，+∞）。故选A。

点评：（1）总体百分位数的估计需要注意的两个问题：①总体百分位数的估计的基础是样本百分位数的计算，因此计算准确是关键;②由于样本量比较少，因此对总体的估计可能存在误差，对总体百分位数的估计一般是估计值而非精确值。（2）确定要求的p%分位数所在区间[A，B），由频率分布表或频率分布直方图知样本中小于A的频率为a，小于B的频率为b，则p%分位数=A+组距×（p%-a/b-a）。