一种基于变径旋转的工质内循环推进装置

摘"要：保证高效推进是星际航行的重要研究内容，为了避免传统推进器燃料与其自身质量的矛盾，Roger"Shawyer、杨涓等前辈设计与验证了无工质微波推进系统，但这种装置的原理存在争议且有着推力过低的短板。基于以上问题沿着该系统的研发思路设计一种基于变径旋转的工质内循环推进装置，同时讨论了推力产生的原理、装置的推力特性、未来可能优化的方向以及衍生问题，并考虑了使用该装置进行姿态控制的可能。

关键词：星际航行；工质内循环；空间推进；微波推进；姿态控制

人类探索宇宙需要有效的交通方式，核能几乎是唯一有星际航行潜力的能源，但目前的推进方式无法充分发挥核能的潜力，主要原因是工质消耗过快。尽管传统推进器的比冲随着新的推进器种类而有所提高，如霍尔推进器［1］，但这些提升幅度仍然不足以进行安全有效的星际航行。因此，设计一个无工质或工质内循环的推进装置成为进行星际航行的迫切需求。为此，Roger"Shawyer、杨涓等前辈设计与测试了无工质微波推进系统（原文中称无工质微波推力器或EmDrive）。根据杨涓团队的结论，其推力与有效微波的最大输出功率以及装置的外形设计［23］有关，但由于微波功率与壁面损耗呈正相关以及腔体大端面直径增加时，腔体的高度降低，使得腔体体积和内壁表面积比降低等因素均会导致品质因数降低。即微波功率以及装置大端面不能无限加大，否则增大的微波壁面损耗以及谐振腔品质因数过低将使得其劣势逐渐大过优势，使推力难以增长。根据杨涓团队的实验数据，其装置在1kW的功率下理论上只有约456mN的推力［3］，距离实用阶段存在一定的距离。目前无工质微波推进原理也存在争议，但可以发现其产生单方向净推力的解释可以理解为通过合理设计人为制造推力差［4］。那么如果考虑放弃无工质微波推进系统的技术原理（即装置原理的经典电动力学解释或光量子解释），转而延伸其人为制造推力差的设计思路，利用其他产生或消除力的方案代替其原有技术原理，就有可能使装置的推力性能提高，进而在理论上达到星际航行的要求。

1"推进装置的基本构成及原理

1.1"推进装置的构成

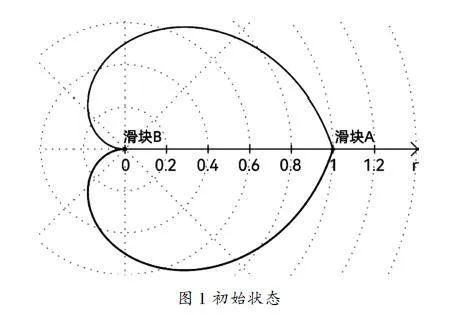
基于以上思想，可以设计一种基于变径旋转的工质内循环推进装置，利用旋转时周期性改变旋转半径的方式改变向心力，继而实现单一方向上的净推力。该装置若采用全电驱动，结合太阳能电池或空间核反应堆［5］，就有可能实现航天器的行星际甚至恒星际航行。该装置由一条带直线电机的水平导轨和旋转机构组成，导轨系统质心与形心重合，位于导轨水平中点上。旋转机构连接电机作为动力源，旋转轴垂直穿过导轨质心。导轨上设有两个连接直线电机次级的滑块A和B，两个滑块之间质量外形完全相同。导轨两侧区域根据滑块名称分为A侧和B侧，初始状态时，滑块A锁止在A侧端点，滑块B锁止在导轨中点，如图1。

1.2"推进装置的原理

某刻，电机通电启动，通过旋转机构带动导轨匀速旋转，此时控制直线电机使两个次级带动滑块A、B以相同速度同向滑动。滑块A向轨道中点滑动，滑块B向轨道B侧端点滑动。当滑块A到达轨道中点时，滑块B到达B侧端点，设完成此动作的时间为导轨旋转1/2圈的时间，至此第一种运动状态结束。完成第一种运动状态后，两个滑块以来时相同的速率沿导轨原路返回，直至恢复初始状态。完成此动作时导轨相比于初始状态刚好旋转了1圈，此为第二种运动状态。以上描述滑块完全按照预定轨迹运动。

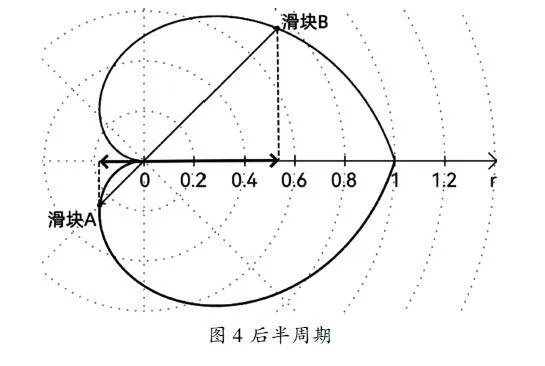
第二种运动状态导轨受力情况与第一种运动状态类似，在规定正方向上所产生的动量在数值上完全相同，故只需分析其中一种场景即可。

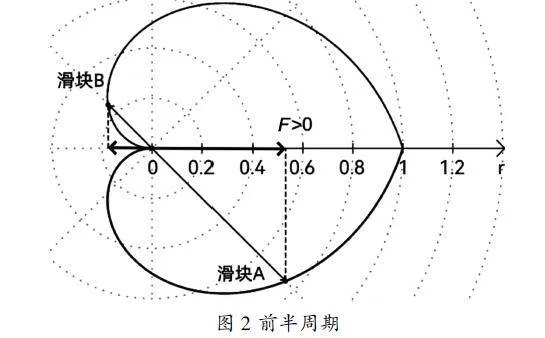
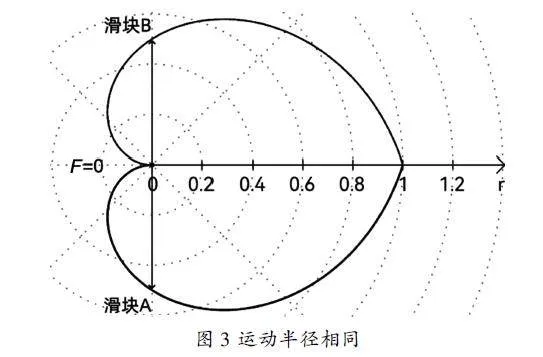
分析上述过程中第一种运动状态，由向心力公式：F=mω2R可知，角速度ω一定的情况下，向心力F只与滑块运动的半径R有关。故当滑块A向内侧运动时，其对导轨施加的力变小，滑块B向外侧运动时其对导轨施加的力变大。设两者向导轨施加的力为FA与FB，导轨受到的力F=FA-FB，沿导轨中点至A侧端点引出一条射线为正方向。可知前半周期FA＞FB，F＞0（图2，取旋转45°为例），当两个滑块运动半径相同时FA=FB，F=0（图3），后半周期FA＜FB，F＜0（图4，取旋转135°为例），但后半周期时导轨已经旋转了至少90°，其初始方向范围已由正方向转为负方向，故导轨受力方向在正方向上的分量为正，导轨受到了单向的力。将负载与该导轨连接，滑块的拉力为整个装置产生推力。

2"推进装置的推力特性

2.1"推力公式分析

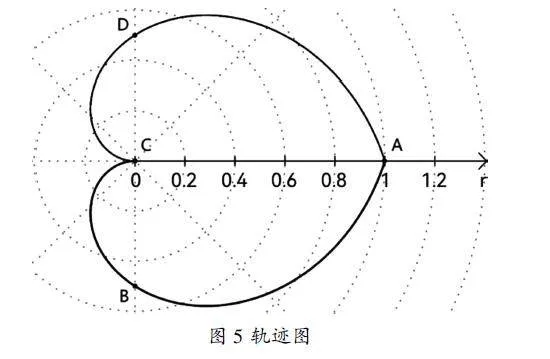
以前文所描述的初始状态为例，设装置在俯视下顺时针旋转，滑块A及导轨A侧作为分析对象，正方向向右，为了方便理解，先写出滑块移动轨迹方程，该函数由两部分组成分段函数：

-πρ=θ，0≤θ≤π

πρ=θ，-π≤θ≤0

图像见图5：

设极轴方向为正方向，极点为导轨中心，图像与极轴的交点为初始点位，即A侧端点，沿极轴引出一条射线，沿极点顺时针或逆时针方向旋转3次，单次π/2，每一次与图像的交点即为一个点位，共4个。滑块沿轨迹运动的过程为：由A侧端点A运动至A侧中点B、由A侧中点B运动至导轨中心C、由导轨中心C运动至A侧中点D、由A侧中点D运动至A侧端点A。

滑块A的前半周期单侧推力系数变化公式为：

（-x/π+1）cosx，0≤x≤π

式中-x/π+1即-（1/π）x+1为滑块运动规律，cosx为滑块A在规定正方向上所产生分力占比的表达式，最终表现为在1/2个周期中推力系数的变化规律，且值域处于0～1，即推力从最低0%至峰值100%。

滑块B的前半周期单侧推力系数变化公式为：

x/πcos（x+π），0≤x≤π

或者在与滑块A的前半周期单侧推力系数变化公式组成分段函数下的：

（x/π-1）cosx，π≤x≤2π

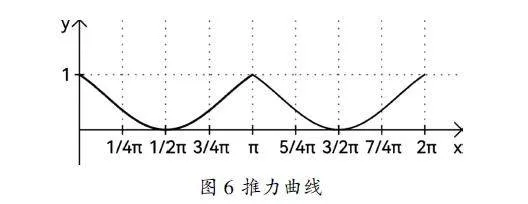
装置半周期推力系数变化公式为：

（-x/π+1）cosx+x/πcos（x+π），0≤x≤π

讨论了滑块的运动后，只需将向心力公式与之相乘便可得到该装置的理论推力曲线，即F推=mω2R，但由于向心力公式所计算的结果为定值，故该曲线仍然为上文提到的推力变化曲线，只是值域有所变化，其最高值为向心力公式的计算结果。

2.2"单周期动量计算

得到推力系数公式后，可以通过对推力系数公式求定积分并除以2π来获取单周期动量常数，与向心力公式相乘即可获得单周期动量公式。

可知应存在两个推力系数公式，但由于滑块A、B运动轨迹对称，故只是替换研究目标而两个公式相同，本次由分段函数来表示全周期推力系数变化公式：

（-x/π+1）cosx+x/πcos（x+π），0≤x≤π

（x/π-1）cosx+（-x/π+2）cos（x-π），π≤x≤2π

推力曲线见图6：

对该公式求定积分（范围：0≤x≤2π）可得动量常数约为2.546/2π，即在稳定旋转状态下，该装置单周期可产生动量约为：

p单=（2.546/2π）mω2R

设质量m为1kg，最大旋转半径R为1m，转速为1rps的条件下，理论上装置可产生动量为：

p单=（2.546/2π）（2π）2≈15.997kg·m/s

根据动量定理，其可等效为1s内持续输出约15.997N的力，再根据动量能量关系式求所需动能：

Ek=ρ2/2m≈127.952J

再由功率公式求功率：

P=W/t=127.952W

即该条件下的装置理论上可以达到约125N/kW的性能，相较于前文中杨涓团队456mN/kW的装置性能更高。

3"推进装置的优化

3.1"装置产生的问题及其解决方案

装置在运转时其实际出力方向为正方向上沿导轨旋转平面两侧各90°。导轨角度越接近正方向出力越高，反之，即出力方向与大小随时在发生改变。这导致装置在工作状态下会出现震动。同时，由于导轨在单向旋转，所以会对负载与壳体施加一个反扭力矩使其沿水平面反向旋转，这些均对装置操控不利。

为解决这个问题，可以使用多套相同的装置组合形成共轴反转系统来抵消装置运行时产生的振动和反扭力矩，并具备一定的姿态控制能力。

3.2"姿态控制系统原理

由于共轴反转系统只是在垂直方向上共轴，而水平方向上两个装置并不能重叠，这就使姿态控制变为可能。姿态控制一共有三个自由度，分别为俯仰、滚转与偏航［6］。默认两个装置水平放置，一上一下结合在一起形成新的装置，这里设装置A在上且顺时针转动，装置B在下且逆时针转动，二者结合形成新的组合体，组合体的质心与形心重合。任意规定一个方向为正方向，该方向上设一个x轴，x轴穿过组合体的质心且分别与两导轨转动产生的平面平行，穿过质心垂直于x轴且与导轨平面平行设一个y轴。

3.2.1"俯仰

进行俯仰操作时，只需要减弱或加强单一装置出力。如使组合体低头，在两个装置出力方向均可在x轴上方向上产生分力时，只需装置A的出力大于装置B的出力，而装置B在x轴方向上出力大于装置A时，则组合体抬头。

3.2.2"滚转

进行滚转操作时，同俯仰操作，不过需要使出力方向在y轴上产生分量，如使组合体左滚转，装置A在y轴方向上的出力就要大于装置B在y轴方向上的出力，反之，装置B在y轴方向上出力大于装置A，则组合体右滚转。

3.2.3"偏航

进行偏航操作时，需要运用前文所提到的反扭力矩。当装置A的转速高于装置B的转速时，组合体向顺时针方向偏航，而装置B转速高于装置A时，组合体向逆时针方向偏航。

3.3"衍生的问题

很明显，上述所有操作均未考虑组合体旋转时的进动、出力点偏离组合体质心而产生的偏心力矩导致组合体产生额外姿态变化。如在俯仰操作时，若改变推力的方式包含转速的改变，即产生了转速差。这必然会造成组合体在产生俯仰力矩的同时产生了偏航力矩，结合上述未考虑的因素，装置在运转时还会出现向左滚转的趋势。综上所述，进行俯仰操作的组合体在低头时会向顺时针方向偏航，抬头时向逆时针方向偏航，同时伴随左滚转。由于装置A、B转速不同导致合力方向不易控制，不利于航行安全。

4"姿态控制系统的优化

4.1"问题总结

根据上述问题，可以发现需要解决两个问题，其一为装置运转时出现的进动及偏心力矩，这个可以通过角动量补偿的方式，如额外加入一套物理性质相同但上下旋转方向相反的组合体来组成四装置共轴反转系统。利用两组反向力矩相互抵消各自带来的姿态影响，或直接外接动量轮等装置来抵消。其二在于改变推力的方式，根据扭矩公式可知，力矩与力的大小以及力臂长度成正比，即我们可以通过改变滑块在导轨上的运动规律来改变力矩，就可以缓解这一问题。

4.2"周期推进效率

根据装置原理不难发现，要想在单个周期获得更大的推力，需要尽可能地增大正方向上的力，减小甚至消除负方向上的力。可知，当滑块位于导轨端点，导轨上的滑块在任意方向旋转180°，这一过程产生的力为最大，而滑块位于导轨中点，无论如何旋转产生的力均为0。这时引入正方向，将最大出力方式用于正方向，最小出力方式应用于负方向，即可达到目的。

很明显，这样做意味着滑块没有运动过程，在导轨划过正负方向交界线的一瞬间，滑块必须在端点与导轨中点之间瞬移，这在当下的时空条件下是不可能的。但上述过程可产生该类型装置单周期最大推力，由于单一滑块在后半周期不产生任何力，且有两个滑块轮流出力，故其表达式可写为：

ABS（sinx），0≤x≤2π

对这整个周期函数进行定积分并除以2π可得，滑块在上述运动状态下装置的推力系数为4/2π，即任意该类型装置推力系数均不会超过4/2π。这里定义装置的推力系数与该类型装置最大推力系数的比值称为周期推进效率。上文讨论的装置周期推进效率约为：

（2.546/2π）/（4/2π）=0.6365

4.3"变效推进以及脉冲式姿态控制系统

通过改变周期推进效率来改变推力的推力控制方式被称为变效推进，若在滚转或俯仰过程中出现偏航现象，可以适当增大相对于偏航方向反方向旋转的装置在负方向上滑块的力臂，即增大该滑块的半径，使其在运动过程中恰好抵消产生偏航的力矩。同时，由于增大了负方向上滑块的半径，也就降低了该装置的周期推进效率，即降低了该装置的推力，继而增大了产生俯仰或滚转的力矩，使姿态控制更为容易。类似于伺服电机的控制逻辑，周期性的力矩调整会使飞行器的姿态发生脉冲式改变，故该类型姿态控制方式被称为脉冲式姿态控制。

结语

本文通过数学建模的方式研究了一种基于变径旋转的工质内循环推进装置，讨论了装置原理、推力特性、作为姿态控制系统的可行性、遇到的问题及其解决方案。可以发现通过合理的设计，理论上该类型装置可以满足工质内循环推进的设计需求，同时具备一定的姿态控制能力。相对于喷气式推进装置解决了不消耗工质无法推进的问题，而相对于无工质微波推进系统，其有着技术原理简单、推力大等优点。如需该类型装置实用化，需要重点研究变效推进中滑块的最佳运动规律以及姿态控制系统的控制逻辑。技术储备方面需要考虑大功率精密直线电机、空间核反应堆等技术，才可能将该类型装置的优势发挥到最大。

参考文献：

［1］朱雄峰，程洪玮，刘阳，等.世界航天发射运输的发展趋势［J］.科技导报，2021，39（11）：4658.

［2］杨涓，王与权，李鹏飞，等.无工质微波推力器推力测量实验［J］.物理学报，2012，61（11）：8894.

［3］杨涓，杨乐，朱雨，等.无工质微波推进的推力转换机理与性能计算分析［J］.西北工业大学学报，2010，28（06）：807813.

［4］祝翔.微波推进电磁发动机推进机理研究［D］.长沙：国防科学技术大学，2016.

［5］薛翔，王浩明，王园丁.国外空间核动力技术发展现状及启示［J］.中国航天，2023（11）：2332.

［6］黄永宁，张晓明.民航概论［M］.4版.北京：旅游教育出版社，2019.

作者简介：罗刚（2001—"），男，汉族，山西大同人，本科，研究方向：推进技术；高春雷（1985—"），男，汉族，江苏南通人，硕士，副教授，研究方向：组合导航与信息融合技术。