统计教学要凸显合理性

一、问题的提出

从小学起，学生就开始接触统计.小学用丰富的案例，让学生体会统计，但仍处于“基于图像的直观判断”阶段，要求学生学会画简单的统计图.初中在小学图像的基础上，开始尝试利用“数字特征”进行统计分析，处于“基于图像与数据处理相结合的局部推断”阶段，要求学生从“直观描述”到“定量刻画”，初步体会数据分析的方法.到了高中，一个案例贯穿始终，让学生通过不同的统计视角，层层深入，反复对比，得出不同的结论，明确统计的结论是对各个统计量综合考察的结果.

学段教材位置学习内容

小学

四年级上第七章条形统计图

四年级下第八章平均数与复式条形图

五年级下第七章折线统计图

六年级下第七章扇形统计图

初中

七年级下第六章数据的收集与整理、条形、折线、扇形统计图、频率与频数、频数直方图、

八年级下第八章平均数、中位数、众数、方差、标准差

高中

必修第二册第九章随机抽样、用样本估计总体

选择性必修第三册第八章成对数据统计相关性、一元线性回归模型、列联表与独立性检验

“成对数据的统计相关性”这一节是在此基础上，从单变量迁移到双变量，学生已掌握数据分析处理的方法，且在信息时代的今天，即使是庞大的数据，也可利用统计软件进行计算处理，因此本节课的重点应该是理解样本相关系数的推导过程，培养学生逻辑推理能力，体会统计学的基本思路与方法，而不是简单的计算.这也是统计教学要凸显合理性的教学需求.因此，本节课的教学目标可设定为：（1）会通过相关系数比较多组成对数据的相关性.（2）会计算样本相关系数，培养数学运算能力.（3）经历样本相关系数的推导过程，培养逻辑推理能力，体会统计的合理性.（4）通过经历“问题提出—公式推导—模型建构—模型应用”的过程，让学生经历数学建模的过程，体会到数学知识的逻辑性和严密性.（5）理解数据统计的基本原则是从直观描述到定量刻画.

统计学通过收集数据和分析数据来认识未知现象的一门科学，因此，统计学具有“不确定性”.正是这种“不确定性”使得很多人觉得统计学具有偶然性，尤其是抽样调查得到的结果，这与数学的“严谨性”、“科学性”不符.而统计的“合理性”则是要引导学生理解统计的意义和基本思想， 结合具体案例，体会知识、 方法背后蕴含的统计思想， 掌握研究统计问题的思维方法，做到真懂会用，实现关键能力的突破，核心素养的落地生根.

二、“成对数据的统计相关性”的合理性解释

1.为什么要学习样本相关系数

研究统计问题的基本路径是直观描述——定量刻画.上节课我们已经学习了用散点图直观判断成对样本数据之间是否具有相关性，今天我们将以定量刻画的方式来学习成对数据的统计相关性.

问题1" 我们回到上节课的案例（人体的脂肪的含量和年龄之间关系），从中可以发现什么？

师生活动：让学生通过观察表格，绘制散点图，从而发现年龄和脂肪含量正相关.

设计意图" 让学生动手操作，绘制散点图，有利于培养学生作图能力.新高考下，对学生作图能力的考察逐渐增加，我们应该在平时的课堂上多给学生练习的机会.而从上节课的案例引出新课，除了温故知新外，更是因为与小学、初中的统计案例丰富不同，高中的统计更讲究一个案例反复应用，让学生通过不同的统计视角，层层深入，反复对比，得出不同的结论，明确统计的结论是对各个统计量综合考察的结果.

追问：我们从散点图中可以看出年龄和脂肪含量正相关，那么，他们的相关程度是多少呢？

师：散点图可以说明变量间有无线性相关关系，但不能精确地说明成对样本数据之间关系的密切程度，更不能精确地说明成对样本数据之间关系的密切程度.因此，我们思考能否寻找一个合适的量来对样本数据的相关程度进行定量分析？这也是我们这节课的任务.

设计意图" 散点图的不足是我们学习样本相关系数的必要性，也是学生的学习动力.这也体现了“研究统计问题的基本路径是从直观描述到定量刻画”.

2.协作方差公式推导的合理性

而统计量应不受问题情境、样本容量、单位的影响，应具有稳定性.因此，学生首先想到的应该是方差，考虑到双变量，可以变形得到1n∑ni=1［（xi－）2+（yi－）2］这个公式，但以此表述是否合理呢？首先，方差可以体现离散程度，但无法描述成对数据到底是“正相关”还是“负相关”.其次，这个公式的几何意义是到点（，）的距离的平方，其图形轨迹是圆，不适合描述“线性”相关.正是因为方差的这两点不合理，引导学生用直线、矩形近似逼近直线.将公式优化为协作方差1n∑ni=1［（xi－）（yi－）］.而（xi－）（yi－）在忽略负号的前提下表示的是两条垂直线段长度之积，其图形指向的是分别以（，）和（xi，yi）为两个对顶点的矩形的面积，更容易逼近直线.

而这部分的推导，教材并未涉及，使得学生觉得协作方差公式给的很突兀，不理解更记不住，从而产生畏难心理.教师在教学中应该强调原因，让公式出来的比较流畅，这也体现了统计的合理性.

3.样本相关系数取值范围的合理性

协作方差公式虽然可以体现样本的相关性，也可以判断正、负相关性，但可以根据具体案例，发现其受单位的影响，所以不能直接用它度量成对样本数据相关程度的大小.从而想到将其标准化得到样本相关系数r=Σni=1（xi－x）（yi－y）Σni=1（xi－x）2Σni=1（yi－y）2.

之后考虑样本相关系数的范围.设“标准化”处理后的成对数据的（x1′，y1′），（x2′，y2′），…，（xn ′，yn ′）的第一分量构成n维向量′（x′1，x′2，…，x′n），第二分量构成n维向量′（y′1，y′2，…，y′n），则有r=1n′′=1n′′cosθ，因为′=′=n，所以样本相关系数r=cosθ.其中θ为向量x′和向量y′的夹角，由-1≤cosθ≤1可知-1≤r≤1.

这种构造向量确定范围的虽然结果明显，但是思维跨度较大，从一个代数公式直接想到n维向量，学生难以理解.

因此，在教学过程中，可以添加这部分的解释.

问题1" 观察样本相关系数的公式，能否化简？

r=Σni=1（xi－x）（yi－y）Σni=1（xi－x）2Σni=1（yi－y）2 = Σni=1xi yi" - Σni=1xi" - Σni=1yi" + Σni=1xyΣni=1xi 2 - 2Σni=1xi" + Σni=12Σni=1yi 2 - 2Σni=1yi" + Σni=12 = Σni=1xi yi" - n - n + nΣni=1xi 2 - 2n + n2Σni=1yi 2 - 2n + n2 = Σni=1xi yi" - nΣni=1xi 2 - n2Σni=1yi 2 - n2.

问题2" 观察样本相关系数的公式，从形式上看有何特征？

分子中n是具体的数，一旦样本确定了，值也就唯一确定了.Σni=1xiyi表示的是对应坐标乘积的和，和之前学习的向量的数量积很类似.分母n2也是具体的数，Σni=1xi 2Σni=1yi 2和向量的模很类似，所以，样本相关系数的公式和n维向量的夹角θ = Σni=1xi yi Σni=1xi 2Σni=1yi 2很相似.从而得到结论-1≤r≤1.当rgt;0时，成对样本数据正相关；当r＜0时，成对样本数据负相关.当r越接近1，成对样本数据的线性相关程度越强；当r越接近0，成对样本数据的线性相关程度越弱.

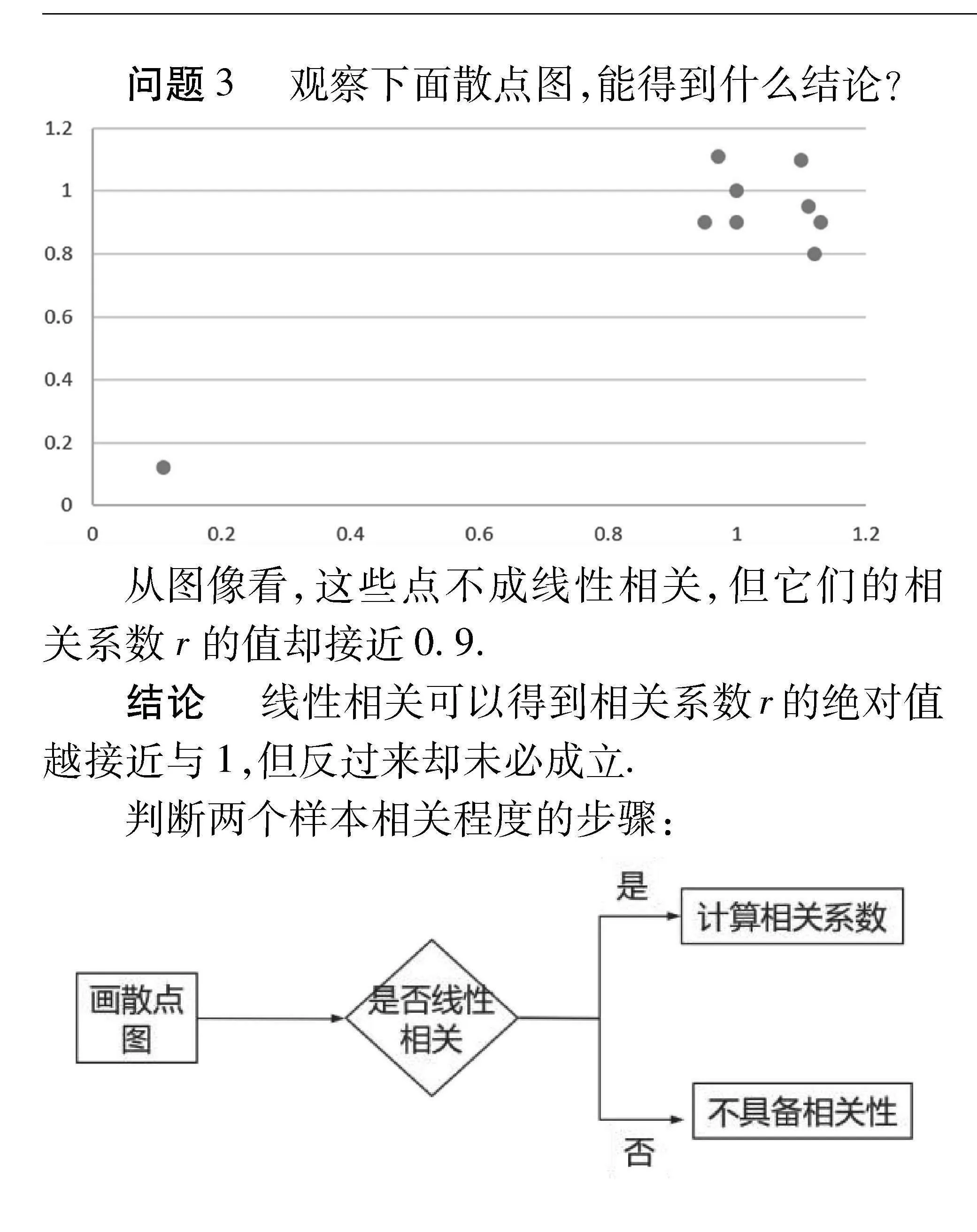
问题3" 观察下面散点图，能得到什么结论？

从图像看，这些点不成线性相关，但它们的相关系数r的值却接近0.9.

结论" 线性相关可以得到相关系数r的绝对值越接近与1，但反过来却未必成立.

判断两个样本相关程度的步骤：

设计意图" 从具体的实例出发，让学生找到矛盾，从而得到判断两个样本相关程度的步骤.另外有具体的反例，学生会记忆深刻.

三、结语

通过小学到高中的学习，学生已经初步建立了样本估计总体的思想，为学生理解用样本相关系数推断变量间的相关性奠定认知基础.统计中刻画数据特征（均值、方差）的一般方法，为构建样本相关系数提供了可资借鉴的思想方法.因此，本节课可以类比单变量，以问题串的形式引导学生推导样本相关系数.让学生体会从“直观描述”到“定量刻画”的过程，将重点放是公式的推导过程，而不是计算，要让学生明白公式如何来？为什么要这样优化？同时，教材对于样本相关系数的推导过程描述的很详细，但为什么优化，没有明确讲，这会让学生觉得这个公式很高端，很难以理解，从而不容易理解.所以，在教学中应该强调原因，让公式出来的比较流畅，这也体现了统计的合理性.