高考数学试题情境的价值、质量与考态分析

摘 要 鉴于试题情境影响测评目的的实现，首先探讨试题情境的测评价值和质量特征，并建构质量特征的分层评价标准。其次，以2024年高考全国卷和地方卷为研究单元，以上述评价标准为研究工具，研究得出高考数学试题情境综合质量的相对排序为：北京卷≈上海卷>新高考I卷>新高考II卷≈甲卷（理科）≈天津卷；虽然高考数学试题的情境存在差异性，但具有以下共性：试题情境主要承载单一的工具或发展价值；真实性与新颖性的水平较低；融合性水平较高。最后，提出重视情境教育、引导学生深度学习的教学建议。

关 键 词 高考数学试题情境；2024年高考数学试卷；情境呈现

曹翛骛.高考数学试题情境的价值、质量与考态分析[J].教学与管理，2025（01）：63-66.

情境是知识+能力+素养测评的重要依托，将试题情境化是推进评价体系转型的关键路径，培养学生核心素养的必然之举，实现立德树人教育根本任务的应有之义[1]。高考作为选拔性考试与教育教学导向的双重载体，其试题的情境化设计能够有效衡量教育成效。《中国高考评价体系》明确了情境是承载高考考试内容和考试要求的重要载体[2]，《普通高中数学课程标准（2017年版2020年修订）》点明了课程教学与考试命题中融入情境元素的重要性[3]。因此，在高度关注高考数学试题情境的基础上，有必要深入探究其内在逻辑与现实规律，全面把握试题的命制理念与方式，确保教、学、评的一致性。本文旨在厘清情境在数学试题中的价值、提炼出高质量情境的主要特征、分析2024年6套高考数学试题中情境考查的具体样态，并据此提出相应的教学建议，以期为一线教学实践提供借鉴与参考。

一、数学试题情境的测评价值解构

试题情境是指以真实的问题为背景，以问题或任务为中心而构成的活动场域[4]，是试题任务的附着点和生长点。情境化数学试题旨在设定一定的时空场域，让学生置身其中，通过调动知识和方法，解决问题并挖掘事件背后蕴含的深刻含义，使数学知识的考核更符合知识产生、知识关联和知识应用的逻辑层次，更利于数学核心素养的测评。

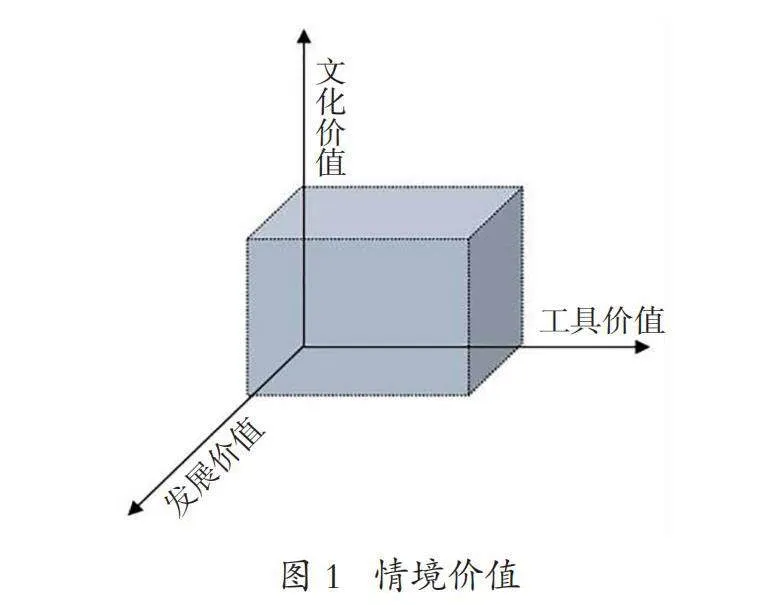
试题情境的测评价值要从数学教育的价值与情境对数学理解的检验价值等方面考虑。数学的教育价值可以分为显性的工具、认识价值以及隐性的文化价值[5]，数学理解又包括工具性、关系性、创造性和文化性等4个理解水平[6]。因此，情境在测评中所承载的价值导向功能：工具价值（知识取向）、发展价值（素能取向）和文化价值（情意取向）。发展价值比工具价值的水平层次更深，即情境发挥发展价值的同时，也发挥着工具价值，遵循“就高不就低”，此时直接定义情境发挥了发展价值。所以，一道试题的情境可能发挥单一的价值，也可能发挥复合的价值（工具+文化价值或发展+文化价值）。本文借助三维坐标系模型可视化展现情境在测评中的多维价值体系（如图1）。该模型中，三个维度分别代表了一种价值，坐标系中的点可以体现不同试题情境所承载价值的类型及权重，坐标轴上和象限中的点分别代表着情境发挥了某类单一或复合的价值。

1.工具价值

数学知识是解决问题的基本工具，体现工具价值的情境用来静态地考查基础知识的简单应用、基本技能的熟练程度。

（2024年天津卷）A、B、C、D、E五种活动，甲、乙都要选择三个活动参加。（1）甲选到A的概率为？（2）已知乙选了A活动，他再选择B活动的概率为？

该题考查条件概率和独立事件等知识。情境为选择参加活动的个人生活情境，情境简单熟悉，是为了服务知识的迁移考查，体现了情境的工具价值。

2.发展价值

复杂综合、真实开放的问题情境可以动态检验学生灵活运用所学知识和非算法化的思维去解决问题的能力，具有发展个人思维、能力和素养等多方面的提升价值。

（2024年上海卷）定义集合M=x0 | x0∈R，x∈（-∞，x0），f（x）<f（x0），在使得M=［-1，1］的所有f（x）中，下列成立的是（ ）。

A. f（x）是偶函数 B. f（x）在x=2处取得最大值

C. f（x）严格增 D. f（x）在x=-1处取得极小值

该题考查了集合和函数的性质等知识。情境为函数型新定义，对函数的奇偶性、单调性、最值等性质需达到关系性理解水平，理解集合的描述含义，根据选项要求进行求证与判断。体现了情境的发展价值。

3.文化价值

文化价值的情境用来传达数学中蕴含的人文精神和德育导向等。从工具和发展的认知价值上升到情意层面，强调渗透正确的国家观、历史观、民族观和文化观等。

（2022年浙江卷）我国南宋著名数学家秦九韶发现了从三角形三边求面积的公式，他把这种方法称为“三斜求积”，它填补了我国传统数学的一个空白。如果把这个方法写成公式，即S=，其中a，b，c分别是三角形的三边，S为三角形的面积。设三角形的三边a=，b=，c=2，则该三角形的面积S为（ ）。

该题考查了秦九韶公式计算三角形面积。情境简单，学生能够容易地实现现场学习与应用，其主要目的在于感受我国古代传统智慧。体现了情境工具价值的同时，更突出了情境的文化价值。

二、高考数学试题中情境的质量特征

一个优质的试题情境应表现出科学真实、适度新颖以及与问题深度契合等多重特征，一套试卷中还需涵盖多样的情境。下面对几个关键质量要素深入剖析，并通过分层的水平界定及具体实例加以说明。

1.类型丰富

课程标准将试题情境分为数学情境、现实情境和科学情境，本文进一步细分为常规数学情境（常规的纯数学问题）、数学探究情境（数学史实和名著等文化情境、新定义、高等数学等情境）、生活生产情境（个人生活、公共常识和生产中的数学情境）、社会情境（地区、国家或全球中的数学情境）和科学情境（自然界或与科学技术相关的数学情境）。通常，情境化试题的范畴主要聚焦于生活生产、社会以及科学等领域，但随着高考数学试题的不断革新，情境化边界也随之不断拓宽。本文所探讨的情境化试题，还包括数学探究情境，即那些以非常规数学情境为载体的试题。

2.科学真实

知识的生成与应用往往嵌套在情境之中，将知识还原到真实情境中去则能够促进知识的深化发展。一个优质真实的情境具有信息复杂、知识综合和结构不良等特点，通过身临其境，唤醒学生问题探究意识，有效培养学生的核心素养。但对情境的真实性并非止于这样的机械化理解，正如前文所说，真实的情境具有非常繁多和复杂的现实变量，在有时间限制的纸笔测试，特别是中高考这样的大规模考试中一般不可复现。当真实情境中的动态要素超越了学生现有认知结构，在必要时也会被合理地简化、等效处理或予以提示。因此，情境的选取都是经过严谨的二次加工，在保留一定真实度的同时科学合理化。基于上述分析，将试题情境的真实性要素划分为三个水平（见表1）。

例如，2022年新高考II卷第3题的情境是关于我国古代建筑中的架举结构模型，所提供的建筑构造描述、示意图和数据完全真实，真实性处于高水平。1998年全国卷（理科）第11题的情境是关于医生与护士向学校分配体检的排列组合模型，并非绝对真实，但容易复现，真实性处于中水平。1979年全国卷（理科）第7题是关于美国物价增长率的情境，其中提到了“如果每年物价增长率相同”，这一条件不符合实际，难以发生，真实性处于低水平。

3.适度新颖

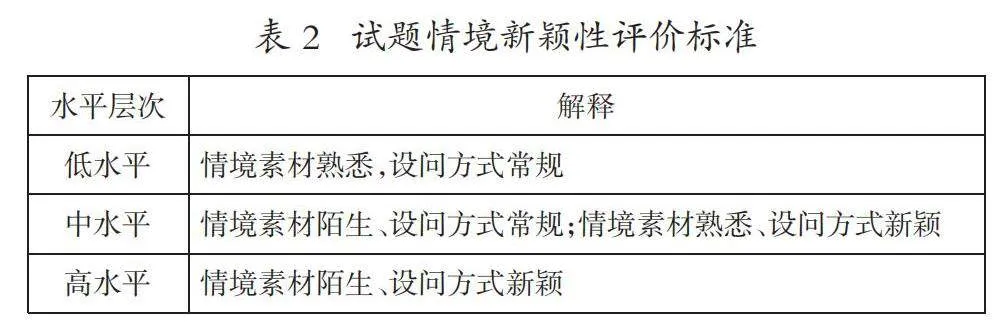
试题情境要具备适切的新颖度。新颖的问题情境能够强化对学生的认知要求，考查学生的应变和创新能力，促进发现、界定和解决问题能力的培养，进而抑制“题海战术”的机械教学，推进指向核心素养的教学。情境素材与问题的设问方式，都是情境新颖性的设置视角[7]。新素材用于搭建试题框架，创设解题条件；新设问用于设置思维梯度，逐步深入，准确区分不同层次的学生[8]。其中，相对新颖的情境素材表现为异于教材和学生学习的常见情境，可以是社会热点、科技前沿、文化史料亦或是新定义等等。试题常见的创新设问方式有开放式、探究式和实践式等。因此，这里将试题情境的新颖性划分为三个水平（见表2）。

例如，前文所述天津卷例题中的情境是熟悉的个人生活实际，设问常规。浙江卷例题中的情境是相对陌生新颖的文化史料，设问常规，两题情境的新颖性分别处于低水平和中水平。2012年湖北理科卷第13题的情境是关于“回文数”的新颖情境，要求自学理解概念之后，探究第2n+1个回文数，新颖性处于高水平。

4.高度融合

融合指的是情境与问题和知识的关联。早年的试题情境存在“两层皮现象”，情境仅仅被作为一个引子，用作修饰，弱化了其测评价值，甚至出现了长篇幅描述与问题解决无关的“情境”。因此，情境与问题要深度契合，二者的融合情况能不同程度地考查学生对情境中信息的提取和加工能力，融合性强弱是评价情境质量的重要视角。融合性实际上反映了情境对问题的作用强度，将其划分为三个水平[9]（见表3）。

例如，2011年江西文科卷第10题，情境是关于凸轮放置直角坐标系中滚动所形成图象的判断，情境中给出了大量凸轮的结构信息和滚动过程描述，这实际上是“鲁洛克斯三角形”，考生需自学理解该三角形的性质进而解决，融合性处于高水平。前文所述天津卷例题中情境为中水平的融合性，浙江卷例题中的情境融合性处于低水平。

三、2024年高考数学试题中情境的考态分析

高考数学卷以《中国高考评价体系》和《普通高中数学课程标准（2017年版2020年修订）》等为命题纲领，相互之间的对比分析具有借鉴意义。本文以2024年新高考I卷、新高考II卷、全国甲卷（理科）、北京卷、天津卷和上海卷等6套试卷为研究单元分析情境的实际考查样态。

1.数据统计与分析

将研究单元中情境化试题的分值占比（情境化程度），情境的价值、真实性、新颖性和融合性进行判别与统计（见表4）。

将表4中的数据概括分析得到以下结论。

第一，从情境类型的丰富性来看，北京卷和上海卷类型最多，均涵盖了三种类型。其中，上海卷以数学探究为主，生产生活和科学为辅，北京卷则以科学生产生活和数学探究并重。其次，新高考I卷有两种类型，以生产生活为主，数学探究为辅。相比之下，新高考II卷、甲卷（理科）和天津卷仅出现了生产生活情境。

第二，从高考数学试题的情境化程度来看，全国卷系列：新高考I卷>新高考II卷>甲卷（理科）；地方卷系列：上海卷>北京卷>天津卷。综合看来，上海、北京卷的情境化程度远高于全国卷（特别是上海卷尤为突出），而新高考卷又高于传统高考甲卷，天津卷远远低于其他卷。

为了便于比较各卷试题情境真实性、新颖性及融合性的质量，将这三个要素的三阶水平依次量化赋分1～3，得到各卷关于上述三个要素的质量得分向量：新高考I卷（1.3，1.7，2.3）、新高考II卷（1，1.5，2.5）、甲卷（理科）（1.5，1.5，2）、北京卷（1.7，2，2）、天津卷（2，1，2）和上海卷（1.5，1.7，2.5）。最后将各卷试题情境的三个要素得分相加，得到它们在真实性、新颖性和融合性上的综合得分：新高考I卷（5.3）、新高考II卷（5）、甲卷（理科）（5）、北京卷（5.7）、天津卷（5）和上海卷（5.7），即北京卷和上海卷高于新高考I卷，新高考I卷高于其他卷。

2.数据反馈与结论

综合情境类型的丰富性、情境化程度和三大要素的质量得分的综合情况，得到高考数学试题情境综合质量的相对排序为：上海卷≈北京卷>新高考I卷>新高考II卷≈甲卷（理科）≈天津卷。将这些概况系统分析可得出以下结论。

高考数学试题情境的共性特征。第一，试题情境主要承载单一的工具或发展价值；第二，真实性与新颖性的水平较低；第三，融合性水平较高。这反映了高考数学卷主要以“低起点”的策略测评学生知识掌握和素能发展情形。

高考数学试题情境的差异表现。高考数学试题的情境设计表现出地域差异性。北京和上海教育相对发达，其试卷在情境创设的类型、数量和质量均处于领先地位。全国卷（新高考I、II卷和甲卷）在这些方面则处于中游水平，照顾的群体更多，均衡满足不同地区教育水平下不同学生的多样化需求，体现了教育公平。这种差异性折射出我国高考命题的多样灵活、选拔人才的公平公正等。

四、教学建议

1.重视情境教育

高考数学试题的考查实态整体上呈现出融合性强、工具价值和发展价值并重的亮点，这对学生从问题情境中阅读与理解、提取与转化信息的能力和数学核心素养等方面的要求较高。需要教师在日常教学中有意识地培养。情境教育是将学习与情境相融合并通过情境演化而优化课程教学的教育活动[10]。教师应学习情境教育的理论、原则和操作要义等，在数学教学中建构具有“形真”“情切”“意远”和“理寓其中”等高质量特征的问题情境，以此来拓宽学生的学习视野，真正培养学生的情境意识与思维张力。

2.引导深度学习

2024年新高考I卷的压轴题以新定义这种数学探究情境的形式呈现，在上海卷中更是占据了主导地位。这类情境极具新颖性与融合性，这启示我们应告别学“死知识”“死技巧”的传统教学，应走向“学会”到“会学”的目标转变，使得学习真实发生。数学深度学习指学生在数学学科内容为主体的情境下，以内在的学习动机，整合学习内容，通过具身式地体验来培养数学高阶思维，达成对数学学习内容结构化理解，将已有知识迁移到新情境中实现数学问题解决的学习状态[11]。教师应引导学生进行数学深度学习，在新授课中塑造数学观念、深化数学理解、启迪数学思想，在复习课中系统化认知结构和发展数学思维与核心素养等[12]。

参考文献

[1][4] 潘红，张亚林.中学化学情境化试题：意义、要素与设计[J].中学化学教学参考，2022（11）：66-71.

[2] 教育部考试中心.中国高考评价体系说明[M].北京：人民教育出版社，2019：35-42.

[3] 中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）[S].北京：人民教育出版社，2020：80-89.

[5] 唐恒钧，佘伟忠，张维忠.什么样的数学和数学教育是重要的——基于义务教育数学课程标准的分析[J].课程·教材·教法，2016，36（10）：58-62.

[6] 李春雷，于凤来.数学理解水平的划分[J].数学教育学报，2022，31（04）： 68-73.

[7] 陈昂，任子朝.高考数学试题情境创新研究[J].中学数学教学参考，2016（13）：2-4+7.

[8] 任子朝.新高考十年数学科考试内容改革：成就、挑战与转向[J].中国考试，2024（07）：11-18+63.

[9] 杨季冬，余莎，王后雄.改革开放以来我国高考化学试题中问题情境的变迁与反思[J] .化学教育（中英文），2023，44（21）：15-22.

[10] 吴刚.论中国情境教育的发展及其理论意涵[J].教育研究，2018，39（07）：31-40.

[11] 张定强，刘成龙，余小芬.数学深度学习：核心要义、内在机制、实践模式[J].天津师范大学学报（基础教育版）， 2024，25（03）：18-24.

[12] 余明芳.为促进数学深度学习而教：理念形塑、模式证析与实践示例[J].课程·教材·教法，2023，43（10）：90-96.

【责任编辑 王泽华】