基于LabVIEW的无模型自适应控制算法实现与应用

摘" 要：为了有效地将无模型自适应控制算法（MFAC）应用于实际场景，该文研究LabVIEW开发环境中实现基于紧格式动态线性化的无模型自适应控制（MFAC-CFDL）。实验结果表明，对于相同的被控对象，LabVIEW实现与Matlab的仿真运行结果一致，证明该方法准确性。进一步与传统的PID控制方法相比较，MFAC-CFDL显示出更强的鲁棒性，并能保证闭环系统的稳定性以及输出误差跟踪的收敛性，通过实验说明该方法工程实践应用有效性和可行性。

关键词：LabVIEW;无模型自适应控制;PID控制;Matlab;紧格式动态线性化

中图分类号：TP29" " " 文献标志码：A" " " " " 文章编号：2095-2945（2024）26-0060-07

Abstract： In order to effectively apply the model-free adaptive control （MFAC） algorithm to the actual scene， this paper studies the implementation of Model-Free Adaptive Control based on Compact Format Dynamic Linearization（MFAC-CFDL） in LabVIEW development environment. The experimental results show that， for the same controlled object， the simulation result of LabVIEW implementation is consistent with that of Matlab， which proves the accuracy of this method. Furthermore， compared with the traditional PID control method， MFAC-CFDL shows stronger robustness， and can ensure the stability of the closed-loop system and the convergence of output error tracking. Experiments show that this method is effective and feasible in engineering practice.

Keywords： LabVIEW; model-free adaptive control （MFAC）; PID control; Matlab; compact format dynamic linearization

如今控制领域学科中控制算法起到一个十分重要的作用，它们被广泛用于自动化、制造、航空航天以及交通运输等行业，用以精确的系统调节、进行性能优化和故障检测[1-2]。很多控制算法理论研究者往往侧重于算法鲁棒性和稳定性等研究，很难应用于实践中，实际工程中传统的PID控制算法仍然占据十分重要的地位，一个重要原因是很多控制算法研究都是基于被控对象数学模型建立起来的，而PID控制算法是基于消除误差的控制算法并不依赖于模型信息，具有十分广泛的通用性和实用性[3-4]。同样无模型自适应控制（Model-Free Adaptive Control，MFAC）是一种数据驱动控制方法，该控制算法不依赖于被控对象的模型，仅利用I/O数据的信息在每个时刻对系统进行动态线性化，通过在线估计控制参数，求得控制量[5-6]。因此MFAC对于系统受到的干扰和系统参数的变化都具有良好的鲁棒性[7]。

LabVIEW是一种基于图形化编程语言的开发环境，其优点在于实时性强，适用于对实时性要求高的应用场景[8-9]。此外，LabVIEW具有良好的和硬件设备结合的功能，因此具有很好的工程实践应用能力[10-12]。Matlab则是一种基于文本的编程语言，其优点在于算法开发便捷，模型解析精确度高。然而，传统控制算法研究往往侧重于科研方面的研究，而缺少实践应用[13-14]。本文采用LabVIEW编程方式，实现了MFAC-CFDL紧格式无模型自适应控制算法。通过对同一被控对象进行验证，并与Matlab仿真结果进行对比，得出了与仿真效果一致的结论，证明了本文设计的控制算法准确性和可靠性。

1" 无模型自适应控制器

无模型自适应控制（MFAC）是控制方法，其核心在于不依赖于被控对象的精确模型，而是基于输入/输出数据信息进行在线估计和控制参数的实时调整，从而实现系统的有效控制。与传统的基于模型的控制系统相比，MFAC的优势在于无需预先建立被控对象的精确数学模型，从而降低了系统设计的复杂性和不确定性[15-16]。MFAC控制器主要包括非线性系统的动态线性化、参数估计和控制律3个关键部分。非线性系统的动态线性化方法主要有紧格式（CFDL）、偏格式（PFDL）和全格式（FFDL）3种，这3种方法衍生出了基于3种线性化的无模型自适应控制方法[17]，使得MFAC在工程实践和科学研究领域中具有广泛的应用前景。

1.1" SISO非线性系统的MFAC-CFDL控制算法

考虑如下的离散时间SISO非线性系统

，（1）

式中：ny，nu分别表示系统输出y（k）和系统输入u（k）的未知阶数，f（...）表示非线性函数，对于SISO系统假设如下。

假设1：系统式（1）对有界的可控输入信号存在有界的期望输出y*（k+1）。

假设2：f（...）关于控制输入u（k）的偏导数是连续的。

假设3：系统式（1）是广义Lipschitz的，即对任意k当Δu（k）≠0，满足Δy（k+1）≤bΔu（k），其中Δy（k+1）=y（k+1）-y（k），Δu（k）=u（k）-u（k-1）且bgt;0。

定理1：对非线性系统（1），满足以上3点假设，当Δu（k）≠0时，存在伪偏导数量ϕ（k），可将非线性系统式（1）描述为如下的紧格式动态线性化模型

，" （2）

式中：ϕ（k）|≤b。

无模型自适应控制方法的控制率可描述如下

式中：μ，λ是权重因子;η，ρ是步长序列，且η∈（0，1），ρ∈（0，1）。

1.2" 无模型自适应控制算法结构

根据无模型控制算法可以绘制经典的无模型控制结构框图，如图1所示。从图中可以清晰地看出，无模型自适应控制系统的控制律与受控系统的阶次和结构无关，而只与系统的输入和输出数据相关。此外，控制律只涉及一个在线调整的控制器参数，即伪偏导数，便于实现。

2" 基于LabVIEW的无模型自适应控制算法程序设计与实现

本文在设计LabVIEW程序时，并没有选择LabVIEW中Matlab Scrip控件，而是为提升控制器的灵活性和扩展性分别创建了u（k）、fai（k）、被控对象子VI，为验证算法鲁棒性和抗扰能力在程序中调用PID控制器，并进行控制效果对比，主程序中调用各子VI函数如图2所示。

其中，u（k）函数用于产成控制信号，基于控制器的参数和当前系统状态进行计算。fai（k）函数为偏导数负责计算控制器的反馈增益，它根据系统状态和控制目标动态调整增益值。被控对象函数则代表实际的被控对象，如机械系统、电路等，它接收控制信号并执行相应的动作或产生相应的输出。

通过在主程序中分别调用子函数，可以实现对整个控制过程的灵活配置和扩展。当需要改进控制算法或添加新的被控对象时，只需修改相应的子函数，而无需对整个程序进行大规模的改动。这种设计方法增强了程序的模块化程度，提高了代码的可读性和可维护性，使得控制系统的开发更加高效和便捷。

2.1" 基于LabVIEW的伪偏导数ϕ（k）实现

在无模型自适应控制中，伪偏导数fai（k）是一个重要的概念。它用于描述系统状态和控制信号之间的关系，并且是自适应控制算法的关键组成部分。伪偏导数函数的计算基于系统的输入和输出数据，通过算法不断学习和调整，以逼近真实系统的动态特性。它反映了系统状态的变化对控制信号的敏感程度，即系统对控制输入的响应速度和方向。

在无模型自适应控制中，由于缺乏对系统内部动态的精确数学模型，因此需要利用伪偏导数来估计和补偿系统的不确定性。通过实时计算和更新伪偏导数，控制器能够逐渐学习并适应系统的变化，从而实现有效的自适应控制。伪偏导数的计算方法通常基于递推估计或滤波器设计等技术，通过最小化预测误差或优化特定性能指标来更新其值。在实践中，伪偏导数的选择和设计需要根据具体的应用场景和系统特性进行定制和优化，ϕ（k）计算为公式（4）

基于LabVIEW实现的ϕ（k）的子VI前面板如图3（a）所示，其中Mu对应控制器μ，Eta对应控制器参数η，后面板如图3（b）所示，其中子VI共有5个输入量，1个输出量。

2.2" 基于LabVIEW的控制量u（k）实现

无模型自适应控制中的控制量u（k）直接作用于被控对象，通过不断迭代计算来调整控制量，以达到最优的控制效果。通过不断采集被控对象的输入和输出数据，并利用这些数据来更新控制量。在每一次迭代中，系统会根据当前的输入和输出数据以及伪偏导数的估计值，计算出最优的控制量u（k），并将其作用于被控对象。控制量u（k）计算公式为式（5）

基于LabVIEW实现的u（k）的子VI前面板如图4（a）所示，其中Rou对应控制器ρ，Lambda对应控制器参数λ，后面板如图4（b）所示，其中子VI共有6个输入量，1个输出量。

2.3" 基于LabVIEW的被控对象模型实现

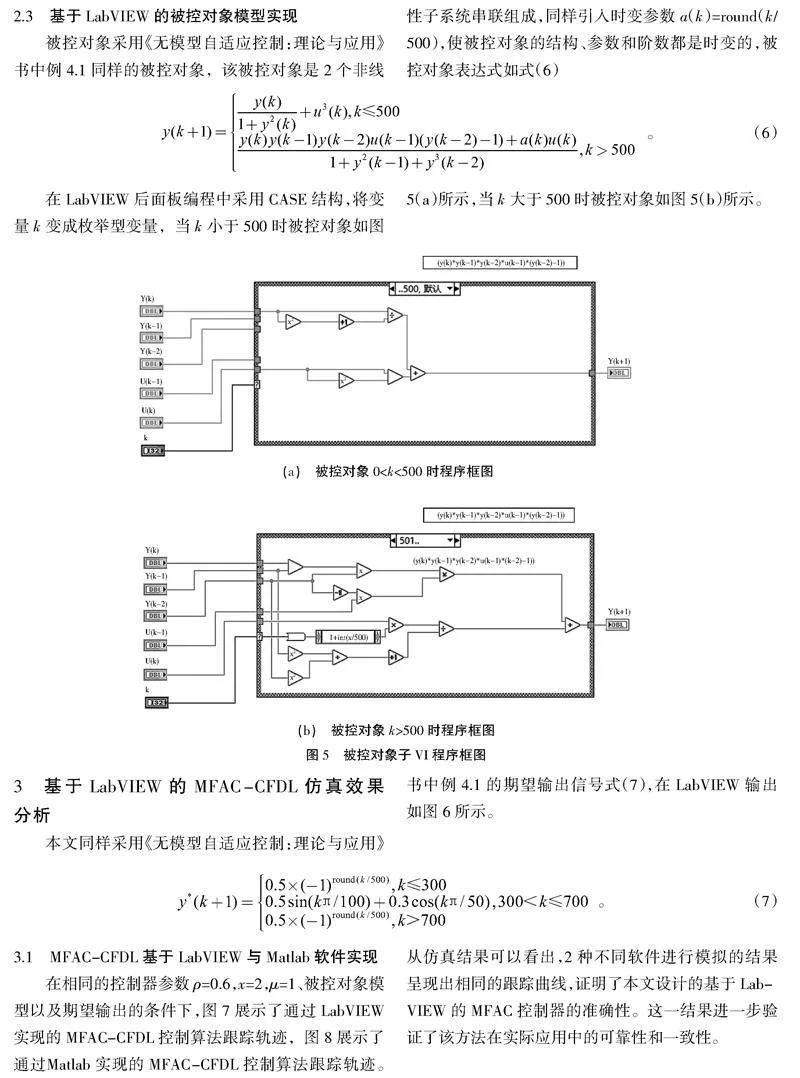
被控对象采用《无模型自适应控制：理论与应用》书中例4.1同样的被控对象，该被控对象是2个非线性子系统串联组成，同样引入时变参数a（k）=round（k/500），使被控对象的结构、参数和阶数都是时变的，被控对象表达式如式（6）

在LabVIEW后面板编程中采用CASE结构，将变量k变成枚举型变量，当k小于500时被控对象如图5（a）所示，当k大于500时被控对象如图5（b）所示。

3" 基于LabVIEW的MFAC-CFDL仿真效果分析

本文同样采用《无模型自适应控制：理论与应用》书中例4.1的期望输出信号式（7），在LabVIEW输出如图6所示。

"3.1" MFAC-CFDL基于LabVIEW与Matlab软件实现

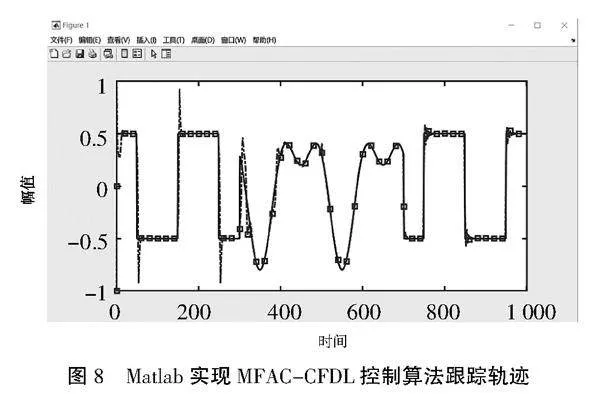
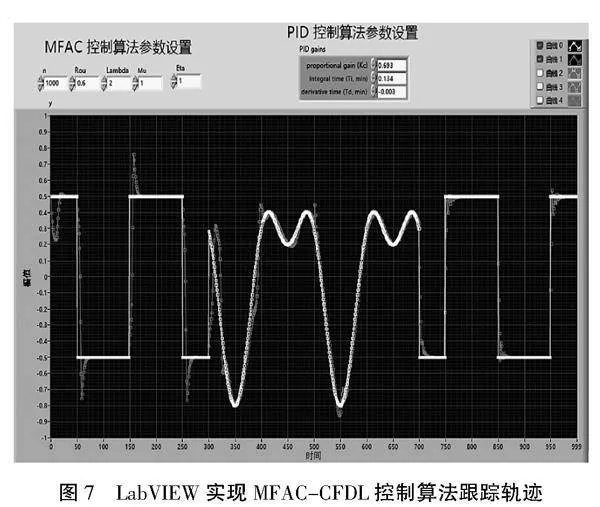
在相同的控制器参数ρ=0.6，x=2，μ=1、被控对象模型以及期望输出的条件下，图7展示了通过LabVIEW实现的MFAC-CFDL控制算法跟踪轨迹，图8展示了通过Matlab实现的MFAC-CFDL控制算法跟踪轨迹。从仿真结果可以看出，2种不同软件进行模拟的结果呈现出相同的跟踪曲线，证明了本文设计的基于LabVIEW的MFAC控制器的准确性。这一结果进一步验证了该方法在实际应用中的可靠性和一致性。

3.2" PID控制算法仿真对比

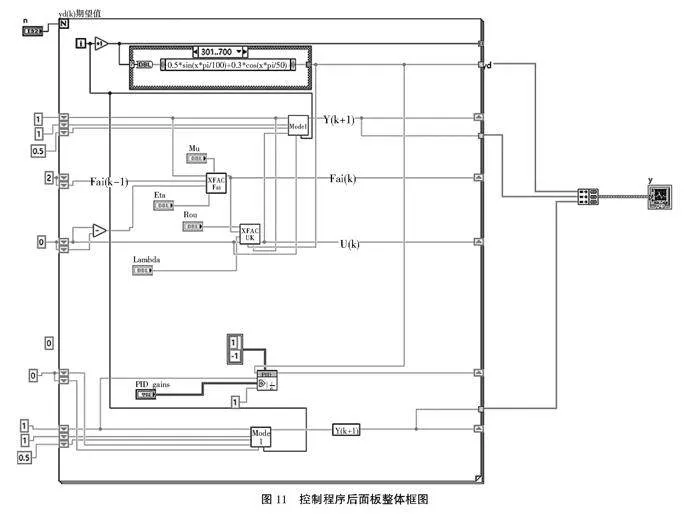
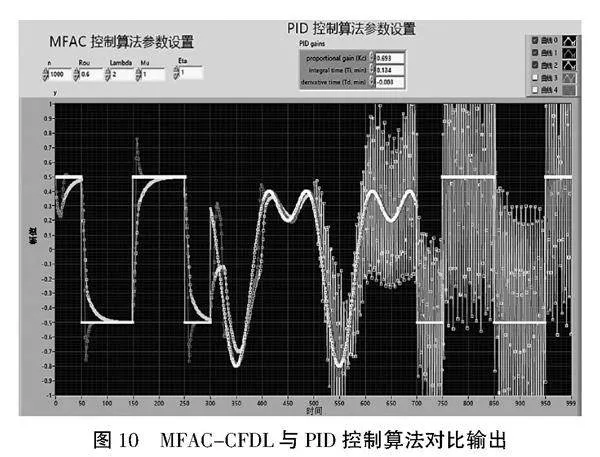
为更好地进行仿真验证工作，本文针对同一被控对象分别采用PID控制器和MFAC-CFDL控制器进行仿真控制效果对比。PID控制是一种常见的控制策略，它通过比较期望输出与实际输出的误差来调整系统的控制量。当误差产生时，PID控制器会根据误差的大小和方向来计算控制量，以消除偏差[18-19]。PID控制具有很多优点，例如容易理解、控制简单、理论背景完善等，PID控制原理框图如图9所示，针对被控对象PID控制器参数进行优化调试后，MFAC与PID控制算法同时输出对比如图10所示，从控制效果可以看出，当被控对象kgt;500后，由于系统引入时变参数a（k），PID控制效果使系统失稳无法起到控制效果，可以看出MFAC控制算法具有很强的鲁棒性。整体程序后面板框图如图11所示。

4" 结束语

在本文中，详细描述了利用LabVIEW的图形化编程环境实现基于紧格式动态线性化无模型自适应控制算法（MFAC-CFDL）不仅能够发挥其实时处理的优势，还能够强化工程实践中的应用能力。通过构建不同的子VI模块，如控制器、估算器和模型等，更加灵活地搭建了整个控制算法的框架。通过仿真测试，验证了LabVIEW实现的控制算法与使用Matlab编写的仿真程序具有一样的效果，并且与PID控制算法进行对比可以看出MFAC-CFDL控制算法对于干扰和系统参数时变情况具有良好的鲁棒性和抗扰能力。因此，该研究对MFAC算法的实践应用具有重要的理论与指导意义，并能够为工程实践领域提供强有力的支持，使得从理论研究到实际应用的转换更为高效。

参考文献：

[1] WANG Q， JIN S T， HOU Z S， et al. Model-free adaptive and iterative learning composite control for subway train under actuator faults[J]. International Journal of Robust and Nonlinear Control，2023，33（3）：1772-1784.

[2] 侯忠生.再论无模型自适应控制[J].系统科学与数学，2014，34（10）：1182-1191.

[3] 曹法立，付远明，吴江涛.基于多级积分分离PID算法的温度控制系统[J].控制工程，2017，24（6）：1107-1112.

[4] 李翔，侯忠生.基于PID参数整定的无模型自适应控制器参数整定方法[J].控制理论与应用，2023，40（10）：1737-1745.

[5] YUE Z，LIJIN F，TANGZHONG S， et al.Model-free adaptive control based on prescribed performance and time delay estimation for robotic manipulators subject to backlash hysteresis[J].Proceedings of the Institution of Mechanical Engineers， Part C： Journal of Mechanical Engineering Science，2023，237（23）：5674-5691.

[6] 侯忠生，金尚泰.无模型自适应控制：理论与应用[M].北京：科学出版社，2013.

[7] 柴逸.吸收式制冷系统的动态建模和学习控制研究[D].天津：天津大学，2018.

[8] 孙军，张鹏，沈卓群，等.LabVIEW环境下的机械臂轨迹跟踪控制算法研究[J].机械设计与制造，2020（6）：245-248.

[9] 刘康，陈娟.一种改进的无模型自适应控制优化方法[J].北京化工大学学报（自然科学版），2023（6）：66-73.

[10] 周雪松，丰美丽，马幼捷，等.基于LabVIEW的自抗扰控制器的设计及应用[C]//中国仪器仪表学会，《仪器仪表学报》杂志社，《国外电子测量技术》杂志社，《电子测量技术》杂志社.2008中国仪器仪表与测控技术进展大会论文集（Ⅲ），天津理工大学自动化学院，2008：4.

[11] 吴异卉，王启志.基于LabVIEW的模型参考自适应控制的实现[J].计算机技术与发展，2008（11）：180-182.

[12] ZHANG X L， ZHOU Y， LIU L， et al. Machine tool spindle vibration monitoring system based on Bluetooth wireless network and LabVIEW[J]. Ferroelectrics，2023：609137-147.

[13] 刘金琨.先进PID控制及其MATLAB仿真[M].北京：电子工业出版社，2003.

[14] 罗建，安会平，李宁.基于LabVIEW与Matlab的滚动轴承故障诊断[J].兵工自动化，2023，42（9）：56-58，82.

[15] HOU Z， ZHU Y. Controller-Dynamic-Linearization-Based Model Free Adaptive Control for Discrete-Time Nonlinear Systems[J].IEEE transactions on industrial informatics， 2013，9（4）：2301-2309.

[16] ZHOU Y， LI M L， LONG Q， et al. Development of a Control System for Permanent Magnet Synchronous Motor Based on LabVIEW and FPGA[J]. SAE International Journal of Advances and Current Practices in Mobility，2023，5（2）：463-472.

[17] 陈琛.无模型自适应控制在大时滞系统中的应用[D].南宁：广西大学.

[18] 苏杰，曾喆昭.非线性时变系统的自耦PID控制方法[J].控制理论与应用，2022，39（2）：299-306.

[19] 叶金鑫，谢丽蓉，王宏伟.非均匀采样系统的无模型自适应准滑模控制[J].电光与控制，2023，30（1）：35-41.

基金项目：2022年度教育部科技发展中心“虚拟仿真技术在职业教育教学中的创新应用”项目专项课题（ZJXF2022017）;2021年度津南区科技计划项目（JNKW202101）

第一作者简介：刘振昌（1985-），男，硕士，讲师。研究方向为先进控制器应用部署。

*通信作者：刘松（1964-），女，硕士，教授。研究方向为虚拟仿真技术应用。