四旋翼无人机设计与滑模控制仿真

尤元+李闻先

摘 要： 随着近些年自然灾害的频繁发生，四旋翼飞行器搜救设备得到越来越广泛的应用。首先介绍四旋翼飞行系统的总体设计架构，然后针对地面坐标系与集体坐标系建立了四轴飞行器的动态模型，同时为得到良好的响应速度、控制稳定度与鲁棒性，应用滑模变结构控制理论设计了飞行器的控制算法。最后通过仿真数据对相同条件下的PID控制器与该控制器对比，证明该控制器的强鲁棒性和控制稳定性满足项目任务需求。

关键词： 四旋翼飞行器； 滑模变结构控制； PID控制； 建模仿真

中图分类号： TN964?34； V249.1 文献标识码： A 文章编号： 1004?373X（2015）15?0080?04

Design of quadrotor UAV and its sliding mode control simulation

YOU Yuan1， LI Wenxian2

（1. Changchun University of Technology， Changchun 130012， China；

2. Changchun Institute of Optics， Fine Mechanics and Physics， Chinese Academy of Sciences， Changchun 130033， China）

Abstract： With the frequent occurrence of natural disasters in recent years， quadrotor UAV search and rescue equipments have been applied widely. The overall design framework of quadrotor aircraft system is introduced. The dynamic model of quadrotor aircraft was established for ground coordinate system and global coordinate system. To obtain fast response speed， and control stability and robustness， sliding mode variable control is used to design aircraft control algorithm. Simulation data are compared between PID controller and the proposed controller， it demonstrates that the strong robustness and control stability of sliding mode variable controller can meet project′s mission requirements.

Keywords： quadrotor aircraft； sliding mode variable control； PID control； modeling simulation

0 引 言

四旋翼飞行器是有四个旋翼呈刚性十字结构的一种飞行装置，它通过控制四个旋翼的速度来实现垂直起降、自主悬停以及姿态控制等动作。因其具有适应复杂环境的能力、可低速飞行、机体结构简单、制造成本低等优点，可广泛应用于军事侦察、自然灾害搜救遥感、高空拍摄等军用与民用领域。随着新型材料的应用、微处理器技术的进步、传感器工艺的提高，电池续航能力的提升以及动力装置的改善，四旋翼无人机成了近几年来国内外研究的焦点[1]。

四旋翼飞行器是一个非线性、强耦合、欠驱动、时变的被控对象，其独特的结构布局和飞行控制的干扰敏感特性使其控制系统的设计变得较为复杂[2]。近些年国内外学者对该飞行器的控制模型做了大量的研究工作，文献[3] 将控制系统分为几个独立的通道，分别设计相应的PID 控制器进行姿态与悬停控制，文献[4]采用反步法，通过构造合适的Lyapunov函数求出控制律进行姿态与位置控制，得到了良好的跟踪性与快速的调整时间。

本文采用滑模变结构控制理论推导了四旋翼无人机动力学模型的控制律，通过Matlab/Simulink对无人机动力模型的PID控制器与滑模控制器进行仿真对比，对比结果表明，本文设计的控制器具有响应速度快、控制过程平稳、无超调与震荡及强鲁棒性等优点。

1 四旋翼飞行器动力模型建立

四旋翼飞行器可视为具有十字交叉固定结构并具有4个独立电机驱动螺旋桨的刚性系统，飞行器的运动完全由4个电机的转速控制，如图1所示。四旋翼飞行器的动力模型输入为4个螺旋桨的转速，输出为飞行器的位置（x，y，z）与飞行器的姿态角（[?，][θ，][ψ]），由于其独立控制变量个数小于系统自由度个数，因此该系统为欠驱动系统、动力不稳定系统。

四旋翼飞行器的简化结构如图1所示，飞行器被视为一个刚体，现做如下假设：

（1） 地面为平坦的且静止不动的近似惯性参考系；

（2） 重力加速度[g]为常数且方向向下垂直于地面；

（3） 大气相对于地球为静止的，且空气密度不随高度改变。

图1 四旋翼飞行器简化模型

那么根据牛顿第二定律有：

[mI00JVBωB+ωB×mVBωB×JωB=FBTB] （2）

式中：[FB]表示机体受力，[FB∈R3；][TB]为机体转动力矩，[TB∈R3；][VB]表示机体的线速度，[VB∈R3；][ωB]表示机体角速度，[ωB∈R3；][J]表示机体的转动惯性矩阵，[J∈R3；][I]表示单位矩阵，[I∈R3]。

由公式（2）可推导得出飞行器的力学方程[5]：

[u=1m（mgsinθ-kd1x）+ψv-θwv=1m（-mgsin?cosθ-kd2y）+?w-ψuw=1m[F1+F2+F3+F4-（mgcos?cosθ-kd3z）]+θu-?v] （3）

式中：[u，][v，][w]分别表示沿机体坐标系[x，][y，][z]轴的机体速度；[kd1，][kd2，][kd3]分别为机体坐标系中沿着[x，][y，][z]轴运动的阻力系数。通过地面坐标系与机体坐标系的坐标转换可得飞行器导航运动方程[5]：

[x=F1+F2+F3+F4m（cosψsinθcos?+sinψsin?）-kd1xmy=F1+F2+F3+F4m（sinψsinθcos?-cosψsin?）-kd2ymz=F1+F2+F3+F4mcosθcos?-kd3zm-g] （4）

式中：[F1，][F2，][F3，][F4]分别代表四个旋翼的升力。

由于每个旋翼的转动惯量相对于转动力矩来说非常小，所以本文忽略了四个旋翼的陀螺力矩，根据角动量定理有：

[dHBdtE=?HB?tB+ωB×HB=TB][HB=JωB=Jxx-Jxx-Jxx-JxyJxx-Jxx-Jxx-JxxJxxpqr] （5）

式中：[HB]代表四旋翼飞行器角动量；[TB]代表作用于飞行器质心的净力矩，定义[TB=u2u3u4]，其中[u2，][u3，][u4]分别代表飞行器以机体坐标系中[x，][y，][z]轴的旋转力矩，[u1]代表四个螺旋桨升力之和，[u1=FT；][p，][q，][r]分别为机体坐标系中每个轴的角速度。

假设俯仰与横滚的角度非常小，那么欧拉角速度可简化为（[?，][θ，][ψ]）T=（[p，][q，][r]）T，通过公式（5）可推导出飞行器的扭矩方程为：

[?=1Jx（F3-F2）l-kd4?-θψ（Jz-Jy）θ=1Jx（F1-F4）l-kd5θ-?ψ（Jx-Jz）ψ=1Jx（F1-F3+F4-F2）l-kd6ψ-θ?（Jy-Jx）] （6）

2 四旋翼飞行器滑模变结构控制设计

滑模变结构控制系统的设计，一般可以分为两个部分，第一个部分是按照某种期望的动态特性来设计切换函数（切换面），设计的切换函数使得开关面有某些优良的品质，从而使系统的状态点可以快速稳定地从滑模面外进入滑模面；而第二部分是设计能在切换面附近产生滑动模态的控制输入。

首先根据飞行器的动力模型可得控制系统的状态方程：

[X=x2u1m（cosx7sinx9cosx11+sinx7sinx11）x4u1m（cosx7sinx9sinx11-sinx7cosx11）x5u1mcosx7cosx9-gx8（Jy-Jz）x10x12+u2Jxx10（Jz-Jx）x8x12+u3Jyx12（Jx-Jy）x10x12+u4Jz] （7）

式中：[X=[x，x，y，y，z，z，?，?，θ，θ，ψ，ψ]T=[x1，x2，…，x12]T；][Jx，][Jy，][Jz]分别为四旋翼无人机在[x，][y，][z]轴的转动惯量。

公式（8）定义误差变量[zi，]然后选取李雅普诺夫函数[Vi：]

[zi=xid-xi， i∈1，3，5，7，9，11xi-x（i-1）d-αzi-1， i∈2，4，6，8，10，12]

[Vi=12zi2， i=1，3，5，7，9，1112（2Vi-1+zi2）， i=2，4，6，8，10，12] （8）

选取滑模切换面[S：]

[Sx=z2=x2-x1d-αz1Sy=z4=x4-x3d-αz3Sz=z6=x6-x5d-αz5S?=z8=x8-x7d-αz7Sθ=z10=x10-x9d-αz9Sψ=z12=x12-x11d-αz11] （9）

那么根据李雅普诺夫到达条件，同时按照指数趋近律的控制方法可以推导得出四旋翼飞行器的控制方程为：

[u1=mcosx7cosx9-εsgn（Sz）-kSz+zd+α（zd-z）+gu2=Jx-εsgn（S?）-kS?+?d+α（?d-?）-Jy-JzJxx10x12u3=Jy-εsgn（Sθ）-kSθ+θd+α（θd-θ）-Jz-JxJyx8x12u4=Jz-εsgn（Sψ）-kSψ+ψd+α（ψd-ψ）-Jx-JyJzx8x10] （10）

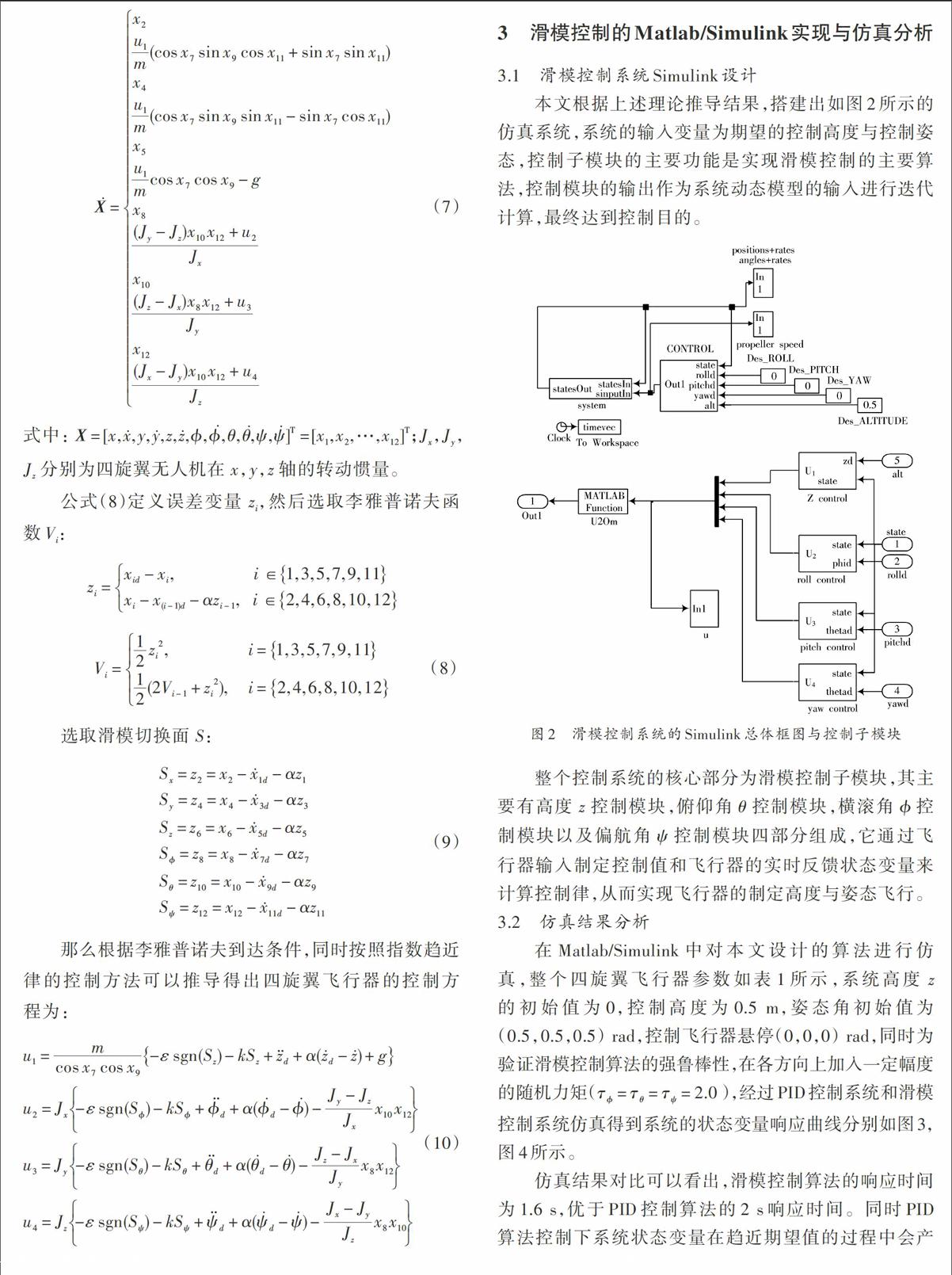
3 滑模控制的Matlab/Simulink实现与仿真分析

3.1 滑模控制系统Simulink设计

本文根据上述理论推导结果，搭建出如图2所示的仿真系统，系统的输入变量为期望的控制高度与控制姿态，控制子模块的主要功能是实现滑模控制的主要算法，控制模块的输出作为系统动态模型的输入进行迭代计算，最终达到控制目的。

图2 滑模控制系统的Simulink总体框图与控制子模块

整个控制系统的核心部分为滑模控制子模块，其主要有高度[z]控制模块，俯仰角[θ]控制模块，横滚角[?]控制模块以及偏航角[ψ]控制模块四部分组成，它通过飞行器输入制定控制值和飞行器的实时反馈状态变量来计算控制律，从而实现飞行器的制定高度与姿态飞行。

3.2 仿真结果分析

在Matlab/Simulink中对本文设计的算法进行仿真，整个四旋翼飞行器参数如表1所示，系统高度[z]的初始值为0，控制高度为0.5 m，姿态角初始值为（0.5，0.5，0.5） rad，控制飞行器悬停（0，0，0） rad，同时为验证滑模控制算法的强鲁棒性，在各方向上加入一定幅度的随机力矩（[τ?=τθ=τψ=2.0]），经过PID控制系统和滑模控制系统仿真得到系统的状态变量响应曲线分别如图3，图4所示。

仿真结果对比可以看出，滑模控制算法的响应时间为1.6 s，优于PID控制算法的2 s响应时间。同时PID算法控制下系统状态变量在趋近期望值的过程中会产生一定量的超调，这在实际控制过程中会增加系统的不稳定性，且在一定的风力干扰下飞行器的姿态会产生抖动。相比较而言，滑模控制算法下的飞行器具有控制过程平稳，响应速度快以及强鲁棒性等优点。

表1 四旋翼飞行器模型参数

[参数＼&值＼&参数＼&值＼&g /（m/s2）＼&9.81＼&[Ixx] /（kg·m2）＼&0.008 6＼&b /（N·s2）＼&3.13e-5＼&[Iyy] /（kg·m2）＼&0.008 6＼&d /（N·m·s2）＼&9e-7＼&[Izz] /（kg·m2）＼&0.017 2＼&[m] /kg＼&0.479 4＼&[l]/m＼&0.225＼&]

图3 PID控制算法高度与姿态响应曲线

4 结 语

本文针对六自由度四旋翼飞行器控制问题，建立系统的欠驱动、非线性系统动力模型，基于李雅普诺夫稳定性理论设计了滑模变结构控制器。在Matlab环境下建立四旋翼飞行器的非线性模型，通过在软件平台下对PID及滑模控制器的系统控制效果进行软件仿真，仿真结果表明，在相同条件下滑模变结构控制器在响应时间、控制过程动态平稳性、鲁棒性方面均优于常规PID控制器，可以达到更好的控制效果。

图4 滑模控制的高度与姿态响应曲线

参考文献

[1] 杨云高.四旋翼无人机地面控制系统的研究[D].天津：天津大学，2011.

[2] 甄红涛，齐晓慧，夏明旗，等.四旋翼无人直升机飞行控制技术综述[J].飞行力学，2012，30（4）：295?299.

[3] LIU Xiaojie， ZHAO Xiaohui， ANAND S， et al. Design and implementation of an embedded control system for small unmanned aerial vehicles： application to a four?rotor mini rotorcraft [C]// 2009 the 4th IEEE International Conference on Industrial Electronics and Applications. Xian： IEEE， 2009： 414?419.

[4] LIU Huanye， LI Jian， YAO Jianguo， et al. Backstepping based adaptive control for a mini rotorcraft with four rotors [C]// 2010 the Second IEEE International Conference on Computer Modeling and Simulation. Sanya： IEEE， 2010： 472?476.

[5] 尤元.四旋翼飞行器控制技术研究及其微功耗设计[D].长春：吉林大学，2013.

[6] SOUMELIDIS A， GASPAR P， REGULA G， et al. Control of an experimental mini quad?rotor UAV [C]// 2008 the 16th Mediterranean Conference on Control and Automation. Ajaccio： IEEE， 2008： 1252?1257.

[7] BOUADI H， BOUCHOUCHA M， TADJINE M. Sliding mode control based on backstepping approach for an UAV quad rotor [J]. International Journal of Applied Mathematics & Computer Sciences， 2008， 4（1）： 12?17.

[8] WU Yiting. Development and implementation of a control system for a quad?rotor UAV [D]. Weingarten： University of Applied Science Ravensburg Weingarten， 2009.

[9] RAZA S A. Design and control of a quadrotor unmanned aerial vehicle [D]. Ottawa： University of Ottawa， 2010.

[10] 孟佳东，赵志刚.小型四旋翼无人机建模与控制仿真[J].兰州交通大学学报，2013，32（1）：63?67.

[11] 聂博文，马宏绪，王剑，等.微小型四旋翼飞行器的研究现状与关键技术[J].电光与控制，2007，14（6）：113?117.