一种新的基于二阶统计量的室内定位方法

饶中初　郭贤生

摘 要： 为了解决复杂室内环境下的近场源定位问题，利用室内小型天线阵列，提出一种近场多径模型下的协方差矩阵匹配及信号子空间匹配定位方法，较好地解决了传统近场源定位算法中无法解决的多径传播问题。一方面，该方法改善了室内定位环境中由于模型失配引起的定位性能恶化问题；另一方面，它也为近场多径环境下的目标定位提供了一种新的解决思路。仿真结果表明，该算法不仅在定位精度上有了较大改善，而且在定位成功概率方面具有较大优势。

关键词： 室内定位； 空间谱； 子空间匹配； 二阶统计量

中图分类号： TN911.72?34 文献标识码： A 文章编号： 1004?373X（2015）15?0018?04

New indoor localization method based on second?order statistic

RAO Zhongchu1， 2， GUO Xiansheng 2

（1. Tongfang Electronic Science and Technology Limited Company， Jiujiang 332007， China；

2. School of Electronic Engineering， University of Electronic Science and Technology of China， Chengdu 610054， China）

Abstract： To solve the localization problem of near?field source in complex indoor circumstance， the localization methods of covariance matrix matching and signal subspace matching based on near?field multipath model are proposed by using small antenna array in indoor， which can better solve multipath propagation problem which can′t be solved in traditional near?field source localization algorithms. These algorithms improved the localization performance deterioration caused by model mismatching in indoor localization circumstance and offered a new solution to object localization in near?field multipath circumstance. Simulation results show that the proposed algorithms have made a great improvement in localization accuracy， and have greater advantage in the aspect of localization success probability.

Keywords： indoor localization； spatial spectrum； subspace matching； second?order statistic

0 引 言

辐射源的波达方向（DOA）估计在电子侦察、智能天线、雷达和声纳等领域有着广泛的应用，已受到人们的高度重视。大量的高分辨阵列测向技术都是运用于室外环境，例如MUSIC算法[1]和ESPRIT算法[2]。然而远场定位技术在近场源场景并不适用，尤其是存在大量多径的室内环境。

指纹库定位技术是一种常见的算法，文献[3?4]将该方法运用于定位远场窄带信号源。由于RSS值在静止环境中都会发生变化，这导致RSS算法的定位精度非常低。文献[5?6]提出了建立信号子空间指纹库提高室内定位精度，但是该算法仅仅考虑了平面波（远场窄带环境），然而在室内环境中，到达天线阵列的波形是球面波而不是平面波，在这种情况下，近场窄带模型比远场窄带模型更有效。

在复杂室内环境中，信道特征表征为复杂的多径传播，信号到达接收阵列为单个信号的不同延时复本，表现为相干多径情况。同时，对有些频段的信号源，其所表现出来的模型特征不再适合于远场窄带假设，如声信号等。

近场信号模型是一种较为有效地描述这种复杂环境信号传播特征的模型，同时考虑到多径及信道的非平稳性等特征[7?8]，其环境背景噪声可建模为非高斯随机过程，如满足冲击噪声等，这时候，传统的基于二阶统计量分析的经典信号处理方法将会带来性能的严重下降，因此，有必要发展基于分数低阶统计量的室内近场源定位理论及高精度定位方法。

本文将对近场源模型下的子空间匹配定位方法进行研究，为室内复杂环境下的近场源定位提供一种可行性解决方案。室内近场多径信号传播模型如图1所示。

图1 室内近场多径信号传播模型

1 均匀圆阵下近场源多径信号模型

考虑[N]根天线的均匀圆阵，圆阵半径为[R]。一个窄带信号包含[q]条多径到达阵列天线。第[l]个阵元的接收信号为：

[xklt=γktst-τkalrk，θk，?k+nlt] （1）

式中：[xklt]代表接收信号的第[k]次反射到达第[l]个阵元在第[t]次快拍时的数据；[γkt]是复系数，代表了第[k]次反射的衰减和相移；随机过程[nlt]是第[l]个阵元接收到的高斯噪声，该噪声是零均值、未知方差[σ2；][L]代表快拍总数。

对于均匀圆阵，近场源的方向矢量[ark，θk，?k]可表示为：

[ark，θk，?k=e-jωrk-d1rk，θk，?k，…，e-jωrk-dNrk，θk，?kT] （2）

式中：[ω=2πλ，][λ]是信号波长；[rk，θk∈[0，π2]，?k∈][[0，2π]]分别表示信号源离基站的距离，到达阵列的俯仰角和到达阵列的方位角；[（?）T]代表共轭转置。

第[k]个信号和第[l]个阵元的距离是[dl（rk，θk，?k）]：

[dl（rk，θk，?k）=r2k+R2-2Rrkρl（θk，?k）] （3）

式中：[ρl（θk，?k）=sinθkcos（?k-（l-1）θ0），l=1，2，…，N，θ0=][2πN]。。。。使用泰勒级数展开，[dl（rk，θk，?k）]可表示为：

[dl（rk，θk，?k）?rk1-ρl（θk，?k）Rrk+1-ρ2l（θk，?k）2Rrk2] （4）

如果信号源处于菲涅尔区域[9]，即信号源到接收阵列之间的距离满足：

[0.62×d3（N-1）3λ12

则方向矢量可表示为[10]：

[a（rk，θk，?k）=exp-jωρ1（θk，?k）R+jω1-ρ21（θk，?k）2R2rk，…，exp-jωρN（θk，?k）R+jω1-ρ2N（θk，?k）2R2rkT]

接收信号可表示为：

[x=As+n] （5）

[式中：][A=[a（r1，θ1，?1），…，a（rq，θq，?q）]，][s=[r1（t）s（t-τ1），…，γq（t）?][s（t-τq）]T，][n=[n1（t），n2（t），…，nN（t）]T]。

2 最大似然估计

假设接收信号[x（t）]采样[L]次，噪声是独立同分布的。高斯随机变量具有零均值、未知方差[σ2，]因此概率密度函数可以表达为[11]：

[p（x（1），…，x（L）A，s，σ2）=t=1L1det[πσ2]exp-1σ2x（t）-As（t）2] （6）

最大似然估计表达式为：

[[σ2，A，s]=argmaxσ2，A，s-NLlogσ2-1σ2t=1Lx（t）-As（t）2] （7）

经过求导和消除常数因子后，上面求最大值的问题等价于如下求解最小值的问题：

[[A，s]=argminA，st=1Lx（t）-As（t）2] （8）

上式的最小值问题，可以通过求解最小二乘解得到[s]的估计：

[s=（AHA）-1AHx] （9）

式中：[（?）H]代表赫米特共轭转置。将[s]代入[[A，s]，]可以得到：

[A=argminAt=1Lx（t）-PAx（t）2=argmaxAt=1LPAx（t）2] （10）

式中：[PA=A（AHA）-1AH]是矩阵[A]的投影矩阵。这样上式可以写成：

[A=argmaxAtr{PAR}]

式中：[tr{?}]是求秩运算；[R]是协方差矩阵估计：

[R=1Lt=1Lx（t）xH（t）]

为了定位信号源，搜索指纹库找到与估计[R]最相似的向量对应的坐标位置：

[l=argmaxPitr{PiR}] （11）

式中：[R]代表实测阶段获得的协方差矩阵；[Pi]是建库阶段第[i]个格点得到的投影矩阵。

3 基于二阶统计量和子空间匹配的定位方法

3.1 信号子空间匹配定位方法

信号子空间定位算法的主要思想是：从协方差矩阵的特征值分解中得到信号子空间，然后建立信号子空间的指纹库。建库阶段，按格点储存最大特征值对应的特征向量[S1；]实测阶段，按照相同的策略得到实测信号子空间[S2]。下面将仔细说明信号子空间匹配技术。

设[S1]和[S2]是[CN×q]的信号子空间，子空间[S1]和[S2]之间的角度为[α1，α2，…，αn∈[0，π2]]。[u=v=1，]定义[6]：

[αk（S1，S2）=arccosmaxu∈S1maxv∈S2uHv=arccosuHkvk，k=1，2，…，q]

其中：

[uHu=vHv=1]

[uHuj=0，j=1，2，…，k-1]

[vHvj=0，j=1，2，…，k-1]

式中：[αk]代表[S1]和[S2]之间第[k]个主角，如果[S1=S2，]则[αk=0]。对比指纹库中的每一个集合，挑出所得值最大的那个集合对应的坐标为发射源的位置。

3.2 协方差矩阵匹配定位方法

协方差匹配算法的主要思想如下：

（1） 在建库阶段，计算[k]个格点的协方差矩阵并用其建立指纹库：

[Ri=1Lm=1Lxi（t）xHi（t），i=1，2，…，K]

式中：[Ri=Ritr{Ri}，][Rfp=[R1，…，RK]]。协方差矩阵归一化的目的是降低建库阶段和实测阶段信号功率的差异，减小对接收信号功率的依赖。

（2） 在实测阶段，接收数据为[xT，]则协方差矩阵为：

[RT=1Lt=1LxT（t）xHT（t）]

式中：[RT=RTtr{RT}]。通过搜索指纹库，在第[k]个位置取得最小值：

[k=argminRkRk-RT22]

式中：[Rk]是第[k]个格点的协方差矩阵，则该坐标对应于目标的位置；[·2]代表最小二范数。

4 仿真分析

仿真在一个20 m×20 m×3 m的区域进行，参考位置的索引如图2所示，发射终端放置在地板上，每个格点之间的距离为1 m。

图2 数据库中参考位置的索引

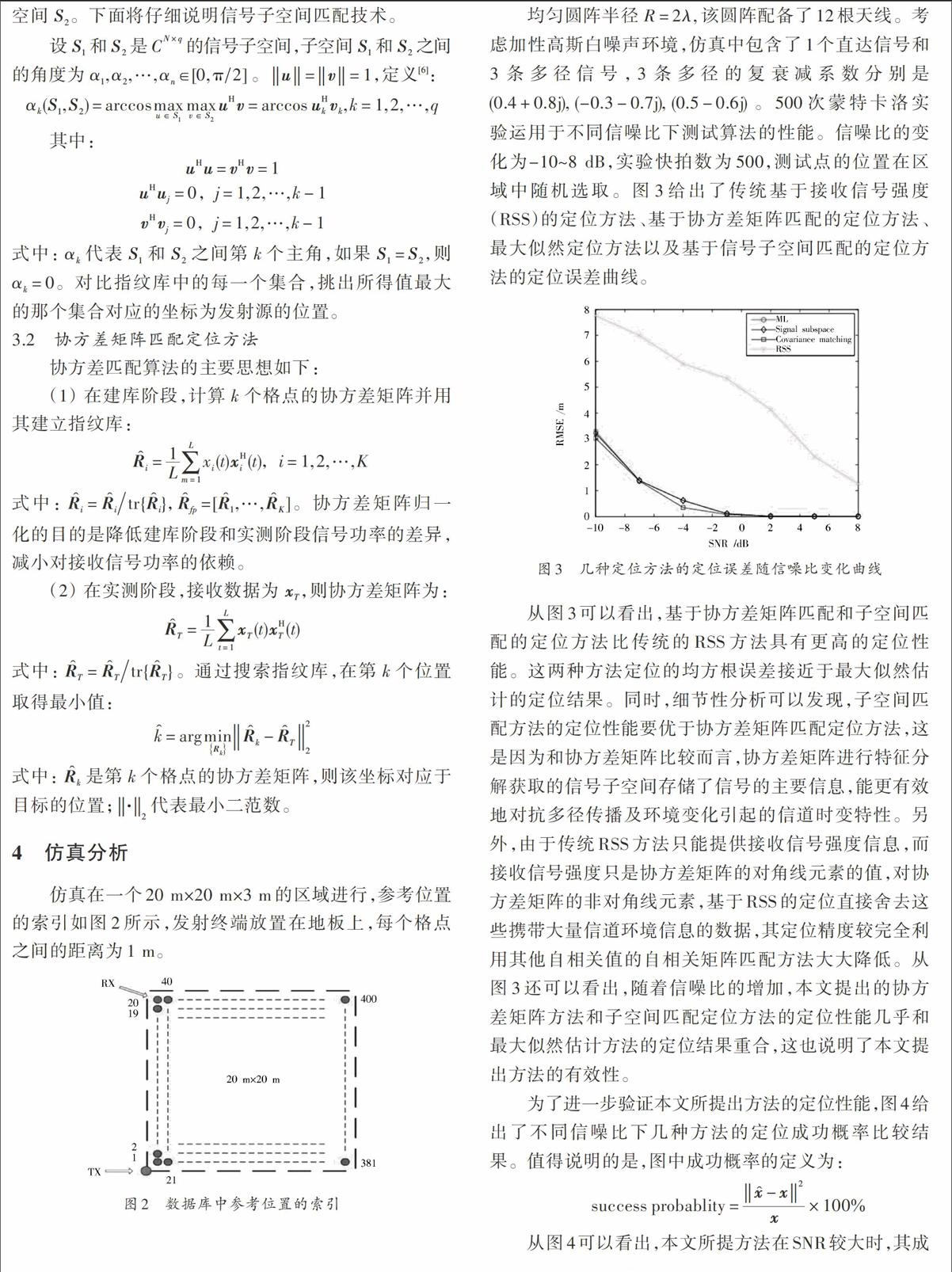
均匀圆阵半径[R=2λ，]该圆阵配备了12根天线。考虑加性高斯白噪声环境，仿真中包含了1个直达信号和3条多径信号，3条多径的复衰减系数分别是[（0.4+0.8j）， （-0.3-0.7j）， （0.5-0.6j）]。500次蒙特卡洛实验运用于不同信噪比下测试算法的性能。信噪比的变化为-10～8 dB，实验快拍数为500，测试点的位置在区域中随机选取。图3给出了传统基于接收信号强度（RSS）的定位方法、基于协方差矩阵匹配的定位方法、最大似然定位方法以及基于信号子空间匹配的定位方法的定位误差曲线。

图3 几种定位方法的定位误差随信噪比变化曲线

从图3可以看出，基于协方差矩阵匹配和子空间匹配的定位方法比传统的RSS方法具有更高的定位性能。这两种方法定位的均方根误差接近于最大似然估计的定位结果。同时，细节性分析可以发现，子空间匹配方法的定位性能要优于协方差矩阵匹配定位方法，这是因为和协方差矩阵比较而言，协方差矩阵进行特征分解获取的信号子空间存储了信号的主要信息，能更有效地对抗多径传播及环境变化引起的信道时变特性。另外，由于传统RSS方法只能提供接收信号强度信息，而接收信号强度只是协方差矩阵的对角线元素的值，对协方差矩阵的非对角线元素，基于RSS的定位直接舍去这些携带大量信道环境信息的数据，其定位精度较完全利用其他自相关值的自相关矩阵匹配方法大大降低。从图3还可以看出，随着信噪比的增加，本文提出的协方差矩阵方法和子空间匹配定位方法的定位性能几乎和最大似然估计方法的定位结果重合，这也说明了本文提出方法的有效性。

为了进一步验证本文所提出方法的定位性能，图4给出了不同信噪比下几种方法的定位成功概率比较结果。值得说明的是，图中成功概率的定义为：

[success probablity=x-x2x×100%]

从图4可以看出，本文所提方法在SNR较大时，其成功概率较高，当信噪比为0 dB时，定位成功概率大于98%。

图4 不同信噪比下各种方法的定位成功概率比较

5 结 论

本文主要介绍了多径模型下的近场源定位问题，利用子空间匹配和协方差匹配方法解决了传统近场源无法解决多径传播的情况。仿真结果表明，本文所提算法不仅在定位精度上有了较大改善，还在定位成功概率方面具有较大优势。

参考文献

[1] SCHMIDT R O. Multiple emitter location and signal parameter estimation [J]. IEEE Transactions on Antennas and Propagation， 1986， 34（3）： 276?280.

[2] ROY R， KAILATH T. Esprit?estimation of signal parameters via rotational invariance techniques [J]. IEEE Transactions on ASSP， 1989， 37（7）： 984?995.

[3] HATAMI A， PAHLAVAN K. In?building intruder detection for WLAN access [C]// 2004 Position Location and Navigation Symposium. [S.l.]： IEEE， 2004： 592?597.

[4] WEISS A J. On the accuracy of a cellular location system based on RSS measurements [J]. IEEE Transactions on Vehicular Technology， 2003， 52（6）： 1508?1518.

[5] TSUJI H， KIKUCHI S， KAVEH M. Indoor localization using subspace matching： an experimental evaluation [C]// Procee?dings of 2006 IEEE Workshop on Sensor Array and Multichannel. [S.l.]： IEEE， 2006： 541?545.

[6] NEZAFAT M， KAVEH M， TSUJI H. Indoor localization using a spatial channel signature database [J]. IEEE Antennas and Wireless Propagation Letters， 2006， 5（1）： 406?409.

[7] ZHI Wanjun， CHIA M Y. Near?field source localization via symmetric subarrays [J]. IEEE Signal Processing Letters， 2007， 14（6）： 409?412.

[8] HE Jin， SWAMY M N S， OMAIR AHMAD M. Efficient application of MUSIC algorithm under the coexistence of far?field and near?field sources [J]. IEEE Transactions on Signal Proces?sing， 2012， 60（4）： 2066?2070.

[9] JOHNSON R C， JASIK H. Antenna engineering handbook [M]. 3rd ed. New York： McGraw?Hill， 1993.

[10] HUANG Y D， BARKAT M. Near?field multiple source loca?lization by passive sensor array [J]. IEEE Transactions on Antennas Propagation， 1991， 39（7）： 968?975.

[11] ZISKIND I， WAX M. Maximum likelihood localization of multiple sources by alternating projection [J]. IEEE Transactions on Acoustics， Speech and Signal Processing， 1988， 36（10）： 1553?1560.