大滞后系统中单神经元PID控制器设计
兰天++杜坚++吉宁++凌景秀

摘 要:首先介绍单神经元PID控制的原理和算法,而后用Matlab语言建立控制器。在二阶大滞后系统中基于单神经元的PID控制存在响应速度慢的缺点,所以用Smith预估控制与单神经元PID控制相结合,对大滞后系统仿真,发现在一定程度上加快了响应速度,并且鲁棒性强。
关键词:PID控制;单神经元PID控制器;Smith预估控;系统仿真;
中图分类号:TP273.4 文献标识码:A 文章编号:2095-1302(2015)05-00-02
0 引 言
PID控制器具有算法简单、鲁棒性较好、可靠性高的特性,因而被广泛运用于各种各样的工业控制中[1],特别在被控对象是线性时不变且方便建立数学模型的控制系统的情况下。然而在工业实际生产过程中,完全的线性时不变系统是不存在的,一般都是非线性时变系统,并且难以建立数学模型,参数整定困难,运用一般的PID控制器控制系统很难达到理想效果。因此本文以研究最基本的神经网络PID控制和单神经元PID控制为主,辅助研究BP神经网络。
1 PID控制的原理和算法
1.1 基于单神经元的PID控制原理
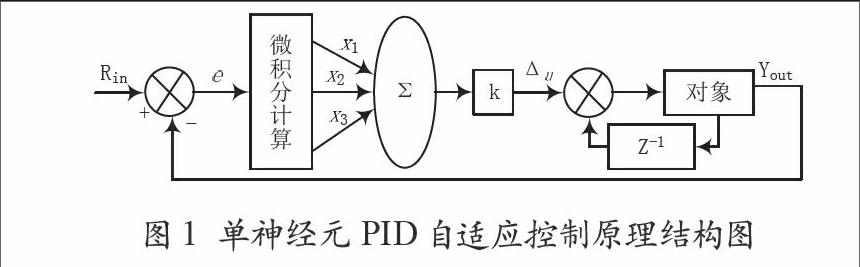
由具有自学习和自适应能力的单神经元构成的单神经元智能PID控制器,不但结构简单,而且能适应环境变化,有较强的鲁棒性。单神经元结构PID控制本质是用单神经元的权系数来代替PID控制器的三个参数[2]。单神经元PID自适应控制,是将单神经元与PID相结合,单个神经元具有自适应和自学习能力,PID控制采用增量式PID控制算法,因此可用单神经元实现PID控制,其原理结构图如图1所示。
图1 单神经元PID自适应控制原理结构图
1.2 基于单神经元的PID控制算法
单神经元PID控制器,是通过在线对加权系数地调整来整定PID的三个参数,实现自适应、自组织的功能。考虑到加权系数应和神经元的输入、输出和输出偏差的相关函数有关,因此按有监督的Hebb学习规则来实现权值的调整。Rin(k)为设定值,Yout(k)为被控对象的输出,经微积分模块计算的三个量X为神经元学习和控制所需的状态量,其控制及学习算法为:
式中:
: 。ηP,ηI,ηD表示积分、比例、微分的学习速率,K为神经元的比例系数,K>0。为了对各个权系数分别进行在线调整,给积分I、比例P和微分D选用不同的学习速率ηP,ηI,ηD。可以通过增大ηI来加快响应速度,但是与之同时超调量也将增大;当超调量增大时可以通过增大ηP来减小超调,但是响应速度将会变慢,调节时间将会增加;增大ηD可以进一步的减小超调,但是调节时间会延迟[3]。
K值的选择非常重要。K越大,快速性越好,但超调量大,甚至可能使系统不稳定。但是当被控对象延时增加时,必须减少K值,来保证系统稳定。K值选择过小,会使系统的快速性变差。
实践表明,在大量的实际应用中,在线学习修正PID参数主要与e(k)和Δe(k)有关。因此将单神经元自适应PID控制算法中的加权系数学习修正部分进行修改,将其中的xi(k)改为e(k)+Δe(k)[4]。
2 仿 真
2.1 大滞后系统
在一些如热工、化工等工业控制中,由于能量或者物料的传输延迟,很多被控对象都具有纯滞后特性。例如,蒸汽控制水温的控制系统,蒸汽量的改变是一个过程量,需要经过一个长度为S的路程才能反映出来。这样,水温要想改变就需要一个滞后时间t。但是附加了纯滞后的被控对象可控度会明显降低,使系统的稳定性下降。一般,当过程的纯滞后时间与过程的主导时间常数之比超过0.5时,该过程被称为大滞后过程。采用常规的PID控制,要达到维持系统稳定的目的,就必须将控制作用变弱,因而在很多地方都不能达到满意的控制效果[5]。
设二阶被控对象为:
考虑到工程实际,取采样时间为1 s,仿真时间为500 s,采用传统PID、Smith预估控制和SNPID(单神经元PID控制)控制对被控对象在Matlab里采用Matlab语言仿真,并在保持控制器参数不变的情况下,改变被控对象参数,分析控制系统的动态性能的改变后得出:传统PID控制大滞后系统很难满足系统的要求,而Smith预估控制和SNPID控制都能很好地控制系统,并且Smith响应速度快于SNPID控制,但是当被控对象参数发生变化或者系统加入扰动时,Smith预估控制的超调量较大,稳定性没有SNPID控制系统好并且Smith预估控制需要获得被控对象的精确数学模型,对模型的变动十分灵敏,这就限制了其在实际工业中的应用。所以当被控对象具有大滞后环节时,可以选择Smith控制或SNPID控制,若被控对象在控制过程中具有慢时变性,可以优先选择SNPID控制。基于Smith预估控制与PID结合的思想,提出SNPID控制与Smith预估控制相结合的方法。
2.2 仿真结果
借鉴Smith预估PID的控制思想,把单神经元PID控制和Smith预估控制相结合,来解决大滞后系统的响应速度和鲁棒性的问题。仿真结果如图2所示。
图2 单神经元PID控制结合Smith预估控制响应曲线
当t=300 s时,被控对象的输出端在0.1的干扰信号其响应曲线如图3所示。
图3 加干扰后响应曲线
当改变被控对象的增益k为4、时间常数为8时,响应曲线如图4所示。
图4 改变被控对象参数后响应曲线
分析图2至图4并和Smith、SNPID对比可得其各项参数对照表如表1所示。
表1 不同方案参数对比
K=2,Tp=2 K=4,Tp=8
Smith SNPID Smith+SNPID Smith SNPID Smith+SNPID
tp(s) 48 150 42 21 81 36
δ(%) 0 0 0 40.2 27.6 28.6
ts(s) 48 150 42 150 290 105
3 结 语
由仿真结果可知在没有超调量指标的前提下,单神经元和Smith预估控制相结合的PID控制器其控制效果优于两种控制方法的单独控制(稳定时间短),当系统参数发生改变时,该控制算法体现出单神经元PID控制抗干扰能力强和Smith响应速度快的优点。因此对于工程中实际的大滞后系统(如炉温控制,一般为二阶惯性环节加延迟环节),运用Smith预估控制和单神经元PID控制相结合的算法能得到不错的控制效果。
参考文献
[1] 蔡自兴.智能控制工程研究的进展[J]. 控制工程,2003,10(1):1-5.
[2] 舒怀林. PID神经元网络及其控制系统[M]. 北京:国防工业出版社,2006.
[3] 张玉浓.神经网络权值直接确定法[M].广州:中山大学出版社,2010.
[4] 阳帅.一种改进的单神经元PID控制器[J].制造业自动化,2010,32(11):119-121.
[5] 徐英.时变大滞后系统的单神经元预测控制[J].清华大学学报(自然科学版),2002, 42(3):383-386.

