一种高效的树形数据存储方法：分段式数字存储

关键词：树形结构；数据存储；算法

0 引言

树形结构数据是一种层次化的数据结构，由节点和边组成，常用于表示具有层级关系的数据[1]。树形结构数据应用于不同领域。比如：（1） 国家行政区划。从省、地、县、乡四级，采用树形结构进行存储能够清晰表现出各级行政区的关系；（2） 公司组织架构。同样是存在上下级关系，完全符合树形结构的关系，采用树形存储容易简化查询、检索以及展示的问题；（3） 商品目录分类。不同商品有不同分类方式，例如在电商网站或贸易网站中经常存在，通过不同类目一级一级地进行检索商品。

树形结构数据在不同领域都有重要的应用价值，能够清晰地表达层级关系，为数据的组织和管理提供了便利。随着信息技术的发展，树形结构数据的应用范围还将不断扩大[2]。本文提出一种基于分段式数字存储的树形数据存储方法，旨在提高树形数据的存储和查询效率。

1 树形结构支持的操作方式

树形结构是常见的非线性数据结构，广泛应用于各种软件开发和数据处理中。树形结构能够有效地表示具有层次关系的数据，如文件系统、组织架构、XML文档等。树形结构的存储方式主要有两种，一是使用特殊连接字符对字符串进行连接，二是在子节点的节点信息中存储父节点以及兄弟节点ID的方式[3]。

第一种方式的操作速度快，但使用存储空间很多，另外当层级多时，会造成节点ID的字符串很长，在一些小型数据库中可能会出现超出字段长度的限制[4]。第二种方式把父节点存在子节点信息中是参考了程序设计中树对象定义的方式进行存储。当在程序中采用这种存储方式，因访问内存的速度很快，所以不存在性能问题。但是当使用数据库进行存储数据，因为访问数据消耗时间较长，当树节点多的时候，性能会成为一个瓶颈[5]。

采用树形结构进行操作，主要包含以下几种方式：

（1） 父节点/子节点查询。

（2） 在树形中插入节点。

（3） 在树形中删除节点。

（4） 在树形中移动节点。

（5） 检索。包含查询同级节点，下级节点，上级节点以及子节点在树中所处的路径。下文会就新的存储方法在以上5种操作的实现以及性能进行分析。

2 常见的存储方式

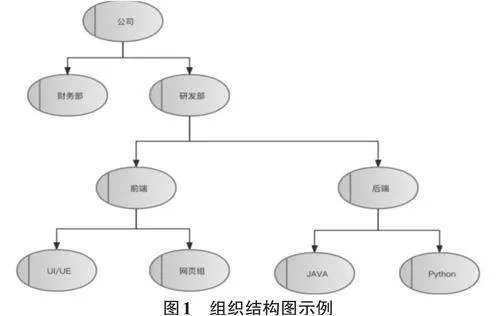
树形结构的数据在数据表中的存储，主要是采用特殊字段存储节点之间的关系。我们经常采用的存储方式有以下两种。以下以组织架构图1为例，介绍两种常见的树形结构存储方式。

2.1 采用分隔符存路径

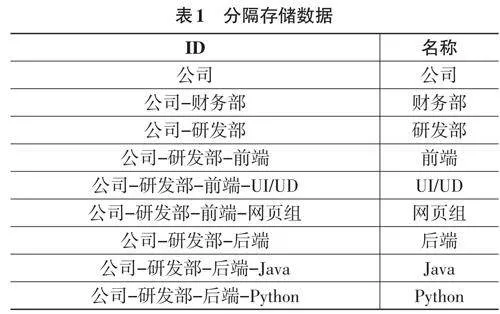
每个节点数据中均增加一个字符串，其中包含父级路径加上子节点的标组成，其中分隔符用不会出现在树节点标识中的特殊字符，例如：._-等字符。例如：公司-研发部-后端-Java组 用来表示当前部门在公司的研发部下包含了一个子部门为后端，Java组处于后端子部门的下面。存储的数据库记录如表1 所示：

这种方式进行存储在操作时非常简单，但是采用字符串进行存储占用的存储空间比较多，且检索时采用的是文本比对速度比数字比对稍慢。

基于目前存储设备的价格大幅下降，占用存储空间的成本影响也比较小，检索速度在数据库中一般采用B树或B+树和检索数字是同一级别，只是比数字检索稍慢一些，所以是一种比较优秀的存储方式。

2.2 存储引用 （parent_id，left_id，right_id）

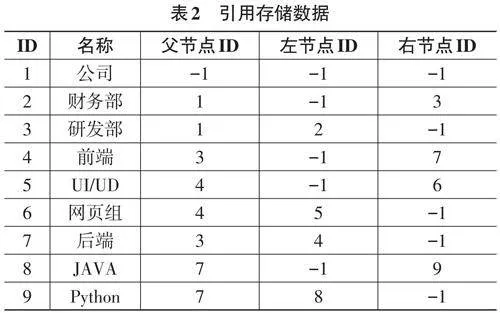
在节点中存储上级节点，左节点，右节点的标识，在某些场景下如果不需要排序则不用存储左右节点。数据如表2所示：

这种存储方式的优点是进行插入节点操作时速度非常快，并且占用的存储空间比较少。但是在删除节点，移动节点以及检索时，需要进行循环查找到对应的数据，多次对数据库进行操作，速度比采用分隔符进行存储要慢比较多。这种方式适用于存储空间比较小的设备，例如某些Android外设、IOT设备等。

3 使用定长数字分段存储

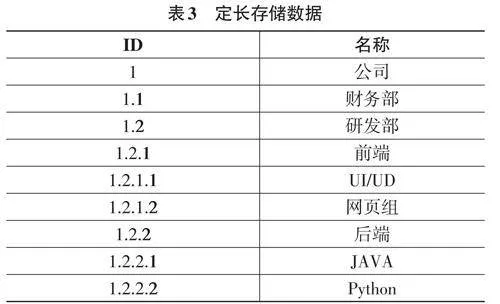
基于以上存储方式，提出一种新方案用于存储树形数据结构。首先采用数字存储节点之间的关系，其次，这数字要描述了节点的完整信息。该方法将一个数字分为三段，分别表示父节点ID、节点ID和子节点ID。在本文中会把节点ID加粗，以用来和父级ID区分开。子节点ID为整个数字在节ID后的数值，例如：1.1.2.0.0.0.0.0， 父节点ID为1.1，节点ID为2，剩余后面为子节点ID。因为子节点ID 均为0，也可以简写为1.1.2。

基于以上考虑，采用一个数字用于存储树，每个字节（8位二进制）作为一级。一个32位的整型数可以用来存储最多四级的树，64位的长整型的数可以存今朝8级的树形结构，考虑到各种情况，我们可以调整每级所占的位数以达到不同的层级效果。数据存储方式如表3所示：

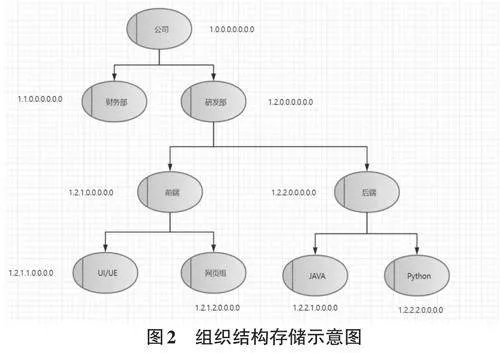
如果用IP地址的方式表示，整个组织结构存储的IP如图2所示：

这种方法进行节点插入，可以快速找到父节点下直接子节点，在容量没超过的情况下可以迅速地插入节点。删除节点时只需要根据ID进行删除即可，性能上是最优的。

3.1 查询父节点

父节点ID即为当前节点的父节点ID部分，直接通过数学运算即可以取得，不用进行数据库查询。

3.2 查询子节点

查询节点ID值在当前节点值和下个节点值之间即可。例上面例子，需要查询研发部下面的所有子节点，即查询ID值在1.2.0.0.0.0.0.0和1.3.0.0.0.0.0.0之间的数值即可。

3.3 删除节点以及子节点

根据上面的条件可以迅速查询出所有子节点以及当前节点，直接使用delete语句即可以一次操作删除所有子节点：

3.4 添加节点

找到主节点下的直接子节点的最后一个，然后在此节点加1，即为要添加的节点的值。

如图，如果要在公司下面添加一个部门：办公室。首先找到所有直接子节点的最后一个节点，即研发部（1.2.0.0.0.0.0.0），下一个节点值为1.3.0.0.0.0.0.0这个值即为新节点的ID值。

3.5 移动节点

移动节点是把整个分枝按原来结构全部移动到另外一个节点下面。如把后端、Java、Python这三个节点按原来的关系移到公司这个节点下面。

步骤如下：

（1） 找到公司可用的子节点ID。根据图公司下面直接子节点的最后一个为1.2，把节点ID加1为新的节点ID：1.3。

（2） 把值从1.2.2.0.0.0.0.0改成1.3。 后端的值变为1.3.0.0.0.0.0.0， Java 的为1.3.1.0.0.0.0.0， Python 为1.3.2.0.0.0.0.0。

一次数据操作即可，不用每个节点进行修改。

这种树形的检索操作是最快的，比前面两种方式均要快，直接使用了数字型的唯一索引进行检索。进行节点插入以及移动节点，比采用分隔符的方式要慢些，存储使用的空间最少。

当树形结构改动较少，主要是进行查询时，这种方式整体性能最好。

4 定长数字分段存储的扩展

上面的采用数字进行存储有自己的缺点：

每个节点下的子节点是有限制的，如果使用1个字节进行存储，那么只能有254个子节点，并且使用64位长整型进行存储时，最多只能存储8级的树。另外一种情况就是子节点的数量过多的时候无法进行存储。

针对这种情况，我们可以把这种固定分组的方式改成动态分配的方式。

针对定长方法的局限性，本文对其进行扩展，提出一种动态分配数据位的方式。以适应更多种情形，根据节点数量使用不同位数表示节点值。

假设节点数为n，则用位数m = ceil（log2 （n + 2）） +1 ，例如有两个节，则使用3位二进制位来表示，最后一位为1用来区分节点。

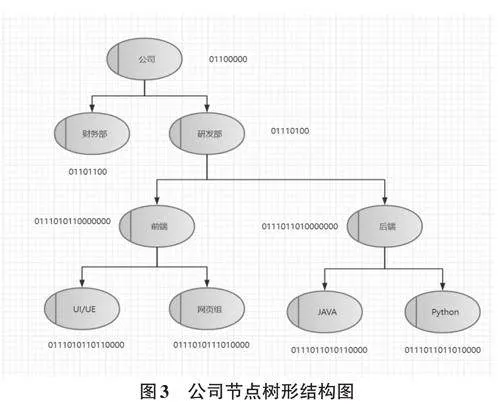
例如公司节点为根节点，根据公式算，m = 3，对应的值为 011，最后一位用作标识，这是第一个节点。公司下有两个部门，依据公式，m=3，对应的值依次为011，101，则财务的ID是011011，研发部为011101，整个树的结构如图3所示。

动态规划的方法和固定使用一个字节作为一级的方式类似，不同处如下：

（1） 使用位（bit）作为最小存储单元而不是byte，如果一级节点少，最少可以使用3位（bit）进行存储，这样增加了层级关系。

（2） 每级使用的位数是动态调整的，如一父节点下的子节点多的话，可以规划更多的位数用于存储。如果节点达到65534，则可以用两个字节（即16位）进行存储。如果有更多，还可以规划出更多位数进行存储。

在树的操作，类似于定长分段存储的方式，规划规划法的算法的计算会复杂一些，整体性能会有一定的下降，但是在检索的时候，性能是一致的。

4.1 查找父节点

因为父节点肯定比当前节点小，因此我们只需要从ID小于当前id值的节点中进行搜索，当节点ID和当前值进行与操作后值还等于节点ID，则节点为当前节点的父节点，其中数值最大的一个为直接父节点：

4.2 查询子节点

查询节点ID值在当前节点值和下个节点值之间即可。例上面例子，需要查询研发部下面的所有子节点，即查询ID值在01110100和01111100之间的数值即可：

4.3 删除节点以及子节点

同上，直接删除当前节点值和下个节点值之间的节点即可：

4.4 添加节点

在动态规划时，如果添加节点所处的父级节点子节点数超过限制时，需要对所有子节点进行动态调整。

添加节点的同定长方式类似，但是当节点数量满的时候需要进行动态调整节点的长度。如上例，公司下面有两个节点，这是三个位值进行存储的最大数量，当要往公司节点下再增加节点的时候，需要动态调整所有子节点。

4.5 移动节点

需要找出所有子节点，然后把原来节点的父节点ID替换成新的父节点ID即可。

5 总结

通过以上内容，我们可以根据不同的场景使用不同的树形实现方式。使用数组分段存储有更好的查询性能以及需要更少的存储空间。

本文提出了一种基于分段式数字存储的树形数据存储方法，并通过实验验证了其有效性。实验结果表明，该方法能够有效提高树形数据的存储和查询效率，尤其适用于节点关系较为稳定的场景。未来工作将进一步研究该方法在不同应用场景下的性能表现，并探索更加高效的树形数据存储方案。