基于Python的数学分析课程可视化和计算教学探索

关键词:数学分析;课程教学;Python语言;可视化;计算
0 引言
数学实验旨在利用软件编程的方式提高科学计算问题的能力,其特点在于增强学习过程的可视性、尝试性和再创性[1]。过去二十多年间,Matlab[2]、Maple[3]和Mathematica[4]等数学软件在教学中得到广泛的应用,并取得了良好的效果。然而,这些软件虽功能强大但价格昂贵,大多数普通高校和科研人员承担不起[5]。因此,选用开源的Python作为数学实验课程的辅助软件是明智之举[6]。Python是目前常用的编程语言之一,具有很强的生命力[6]。Python语言以其简单易学、面向对象、免费开源等特点著称[7],并拥有丰富的第三方库支持,可应用于数据分析、机器学习、人工智能等多个领域[6]。
1 基于Python 的数学分析课程实验教学的意义
数学分析是古典微积分的核心内容,是学习专业基础课、专业课的一块基石,在科学技术中有广泛应用。通过学习,提高学生的逻辑推理能力、抽象思维能力及计算能力,增强基本技能,扩大视野,陶冶情操,进而提高数学素质与数学修养。然而,当前数学分析课程教学普遍存在授课形式单一、学生学习兴趣不高等问题。数学分析课程内容抽象复杂,部分学生难以理解,甚至产生畏难情绪。因此,有必要积极探索新的教学思路和方法,以提升教学效果。借助Py⁃thon进行可视化实验和复杂问题计算,可以使学生的理解更加直观,提高学习积极性[8]。
1.1 Python 编程成为必备技能
随着大数据、人工智能等技术的快速发展,编程技能已成为相关领域从业人员的必备技能[6]。目前,我校所有理工类专业均开设Python程序设计课程,对学生进行编程教育。在数学分析教学中若融入Py⁃thon的可视化、仿真和建模等,不仅使学生对相应的数原理的思考更深入透彻,而且对学生提高动手实践能力方面也有帮助。
1.2 改善理论教学枯燥性
传统教学模式下,教师难以兼顾所有学生的个体差异,容易导致部分学生学习积极性不高。Python语言的图像功能有助于学生减轻学习畏难心理,加强理解和对比。图形可视化可以将抽象的数学概念以更直观、有趣的方式呈现,激发学生的学习兴趣,同时也有助于教师兼顾不同学生的学习需求。
1.3 提升数学建模能力
数学课程教学普遍注重理论知识的讲解,而忽视与实际应用的结合,导致学生缺乏感性认识。利用Python软件进行数学建模,可以培养学生的建模意识和编程能力,并帮助他们解决实际问题。这不仅使得课堂教学更生动形象,也会提升学生解决实际问题的能力。同时,学生数学建模能力也将得到进一步提升,向专业更深领域发展。
2 基于Python 的可视化和计算教学案例
本节将通过典型案例,介绍如何利用Python 的SymPy、Math、SciPy、NumPy、Matplotlib 等第三方库进行函数绘图、极限计算、导数和积分计算等操作。案例实验环境是Windows11+Python3.9,所用函数来自华东师范大学编写的《数学分析》教材(第五版)[9]。
2.1 绘制图像
Python可以绘制二维和三维图形,例如一元函数的二维图像、二元函数的三维图像以及空间曲线等。
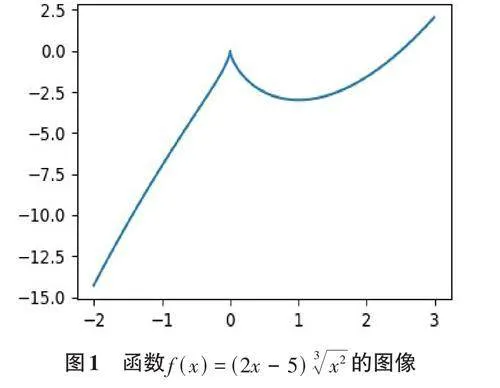
例 1:绘 制 f (x) = (2x - 5) 3 x2 在 [-2,3] 上 的图形。
2.2 了解函数分布
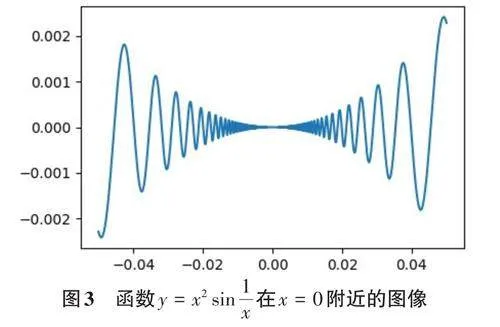
函数极限的概念较为抽象,部分学生难以理解。以涉及无穷大、无穷小和有界函数的极限为例,传统的板书和语言描述难以清晰地展现函数的变化趋势,而Python的可视化功能可以弥补这一缺陷,帮助学生直观地理解极限的概念。
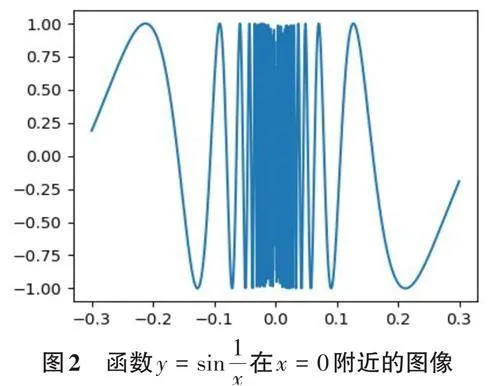
结果展示如图2, 当x → 0时,函数值在区间[-1,1] 来回振荡,越接近0,振荡频率越高,但并不趋于0。从图像看,越来越快地振荡而不停止,故可理解不存在极限。
2.3 计算极限
求极限的命令是limit(f,x,x_0,dir) ,其四个参数分别是:函数或数列极限表达式,极限的变量,变化的趋势和极限的方向。dir =‘+ ’, dir =‘ -’分别表示右、左极限。注意:Python符号运算时应先加载数学符号函数库SymPy。
2.4 计算导数或偏导数
求微分关键是求导,此处仅讨论求解函数导数,可以利用SymPy包的命令diff来完成,语法是: diff(f,x,alpha) ,其中f为求导函数,x 为自变量,alpha为求导的其他设置,如阶数等。很多时候,自变量还有特定的值,可以进行表达式代入值的求导,这时需要定义函数,通过evalf方法传入x 的数值。
2.5 计算函数的积分
在Python中,使用SymPy包可以计算微积分,主要通过integrate方法计算,语法是: integrate(f,(x,a,b)),其中f为被积函数,x为自变量,a,b分别为上、下限。
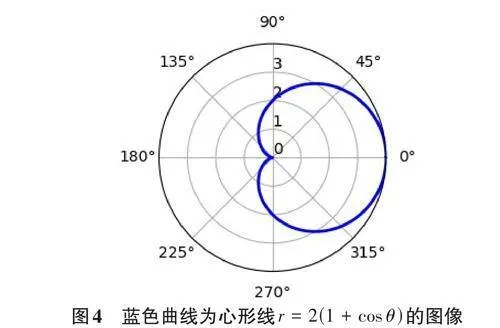
对于比较复杂的积分,部分学生缺乏空间想象力或绘图能力,难以绘制积分相关图形,找不到积分区域或积分限。有些学生则对积分公式或方法掌握不牢,无法或很难计算。以下通过心形线的例子,计算心形线长度及其所围面积。
例9: 已知心形线r = 2(1 + cosθ ),求它的弧长和所围图形的面积。
2.6 计算曲线积分和曲面积分
由于Python目前缺乏直接计算曲线积分和曲面积分的函数,通常需要利用数学公式将其转换为定积分或二重积分进行求解。曲线积分所对应的定积分被积函数往往较为复杂,可以使用 SciPy 库的 inte⁃grate.quad() 函数进行计算。类似地,曲面积分所对应的二重积分可以使用 integrate.dblquad() 函数进行计算。
3 结论
Python 语言应用广泛,几乎涵盖了所有程序领域,被誉为“胶水语言”。自2013年起,越来越多的高校开始面向非计算机专业开设Python语言编程课程。上述分析和案例实践表明,Python 软件可以有效辅助数学分析课程教学,帮助学生理解抽象的理论知识,并将其应用于解决实际问题。尽管Python在计算复杂积分等方面仍有提升空间,但其作为一款免费开源软件,拥有强大的社区支持和持续更新的能力,未来发展潜力巨大。本文探讨了Python在数学分析实验教学中的应用,旨在帮助学生更好地理解和应用所学知识,并掌握 Python的编程思想。在未来就业市场中,数学专业毕业生需要具备一定的计算机和软件操作能力。因此,将Python融入数学专业课程教学,是顺应时代发展趋势、提升人才培养质量的必然选择。

