数学学科核心素养视角下“数列”教材内容比较研究

［摘 要］ 文章从章节结构、内容表征和内容呈现等方面比较两版教材中的数列知识内容，得出新版教材的特点：注重数学知识的整体构建，促进数学思维素养的发展；注重知识系统与训练系统的整体设计，促进数学方法素养的提高；注重问题情境的全面丰富，促进数学工具素养的提升.基于新版教材的特点，文章提出教学建议：注重“四基”，构建知识结构体系；发展“四能”，内化数学研究方法；强化“三会”，提升数学学科核心素养；变革方法，切实促进学生发展．

［关键词］ 高中数学；教材；数列；比较研究

基金项目：广东省基础教育学科教研基地项目，广东省于涛名教师工作室，广东省教育科学规划课题“基于SOLO分类理论的高中数学学业质量评价的实践研究”（2021YQJK103）.

作者简介：于涛（1982—），本科学历，中学高级教师，广东省名教师工作室主持人，从事数学教育教学研究工作.

教材作为连接课程标准与课堂教学的重要媒介，是落实课程改革理念的载体. 为了在新课程教学实践中更有效地发挥数学教材的作用，并贯彻数学学科核心素养，本文采用统计分析法和文本分析法，对人民教育出版社2019年出版的《普通高中教科书数学选择性必修第二册（A版）》（下文简称新版教材）与2004年出版的《普通高中课程标准实验教科书数学必修5（A版）》（下文简称旧版教材）中的“数列”知识内容进行了比较研究. 本研究旨在为新版教材的运用提供有价值的参考.

研究框架

根据教材编写内容，从宏观和微观两个层面，分章节结构、内容表征和内容呈现三个维度对教材进行定性或定量分析. 具体比较两版教材在章节结构、栏目设置、素材选取、知识编排、例习题编排等方面的情况，分析新版教材的特点，提出教学建议.具体教材比较研究框架如图1所示.

教材内容比较分析

1. 章节结构比较

比较两版教材中数列知识内容的章节结构，详见表1.

数列作为函数主线的内容之一，新版教材在编排逻辑上类比函数知识内容，按照“一般数列→特殊数列”的顺序，将数列知识内容由旧版教材的5节整合为3节，突显了函数主线中不同知识内容之间的内在逻辑联系以及研究方法的连贯性；新版教材将数学归纳法与数列知识内容整合为一个章节，把教学重点从证明不等式调整为证明与数列、恒等式紧密相关的数学问题. 具体比较发现，前n项和公式的定义从旧版教材的2.3节调整到新版教材的4.1节，一是完整呈现“一般数列”的研究路径，为两类“特殊数列”的研究做好铺垫；二是深化对数列作为特殊函数的全面理解，通项公式是函数，前n项和也是函数；三是渗透运算是研究数学对象的重要方法，通项公式是直接的研究对象，前n项和是经过运算得到的研究对象.新版教材对数列知识内容的重构，更加注重整体性，有助于帮助学生构建更为完整的知识体系.

2. 内容表征比较

（1）栏目设置

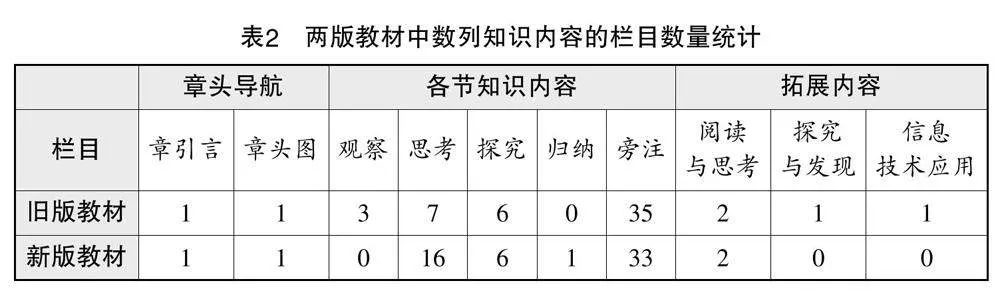
两版教材在数列知识内容的总体结构呈现上，均遵循“章首导航→各节知识内容→拓展内容→小结→复习参考题”的顺序. 本文对两版教材的栏目设置进行了统计，结果如表2所示.

从统计数量来看，新版教材中的“思考”栏目的数量约为旧版教材的2.3倍，更加注重以问题的方式引导学生进行深入思考，凸显“问题导学”理念，培养学生理性思维；新版教材在“思考”“探究”“归纳”等栏目中多次使用“仿照”“类比”等词语，借此来渗透类比、特殊与一般等思想方法，引导学生积累并运用数学活动经验，培养学生迁移能力；新版教材删除了“估计的值”“九连环”“购房中的数学”等拓展内容，丰富了“斐波那契数列”，新增了“中国古代数学家求数列和的方法”，使数学文化的内容与知识联系更加紧密，增加了教材的趣味性与可读性.

（2）素材选取

素材作为数学教学的重要载体，可以使数学教学具有开放性、多元性、动态联系性. 本文对两版教材的素材选取情况进行了统计，结果如表3所示.

从统计数量来看，新版教材的素材总数略少于旧版教材.其中，文化素材的数量增加了6个，使得涵盖的国家或地区从原先的7个扩展至10个，这有助于拓宽学生对数学及其文化背景的认识，让他们体会到数学如何植根于文化之中，并进一步推动文化的进步. 同时，生活素材的数量减少了12个，删减了不能更好地反映数列本质的“高中生人数”“人民币面额”“水库水位”等素材，精简了“银行存款”“购房问题”“人口问题”等反复出现的素材，增加了“天坛圜丘坛”“理财产品”“新能源汽车”“教育网站”等富有时代气息的素材，体现了数学与现实生活广泛且密切的联系.数学素材增加了2个，分别是“除数函数”“欧拉函数”等数学新定义素材，更加强调数学课程学习情境的重要性.

（3）图表设置

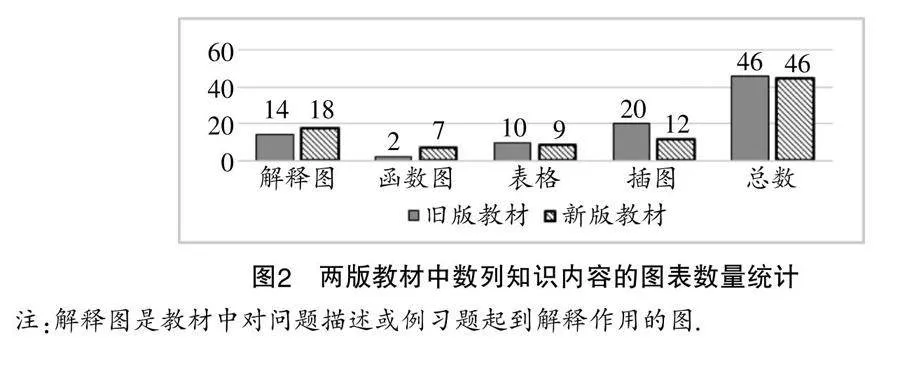
图表作为表征数学知识的重要工具，可以使学生直观、形象地理解抽象的数学概念与性质［1］. 本文对两版教材的图表设置情况进行了统计，结果如图2所示.

从统计图表来看，新版教材精简了仅用于丰富教材画面的插图，为旧版教材的60%，增添了辅助教学的解释图和函数图. 新版教材中有3幅图用于展示数列的表示方法，2幅图用于阐释等差数列和等比数列的通项公式与函数之间的关系，2幅图用于探究数列的性质. 这些函数图的多角度应用，充分体现了新版教材始终贯穿函数主线的教学理念，强调了函数思想与方法的实际应用.

3. 内容呈现比较

教材内容的编写体系分为知识系统和训练系统，知识系统包括研究路径、问题情境、产生发展、方法思想等，具体呈现即知识编排；训练系统包括例题、练习、习题（包括变式、拓展、延伸）等，具体呈现即例习题编排.

（1）知识编排

本文对两版教材的知识编排（必学内容）进行了比较，结果如表4所示.

由表4可知，新版教材按照“背景—概念—表示—性质—求和公式—应用”的研究路径编排知识［2］，强调等差数列与等比数列学习过程的相似性.新版教材在数列概念引入环节中的素材均呈现出两组数之间的对应关系，为理解数列是定义在正整数集或其有限子集上的一类离散函数的本质提供了实际情境基础，情境设置更加恰当.新版教材更注重概念、方法的生成过程，对等差、等比数列概念的编排，紧扣“运算（减法、除法）”这一核心，从“数”到“项”，逐步完成两个特殊数列取值规律的归纳与抽象；对等差数列前n项和的编排，从高斯问题到特殊数列｛ｎ｝，再到一般等差数列｛ａ｝的求和公式的推导，引导学生从特殊到一般，在方法简化的情形下自然而然地发现新方法.新版教材更强调数列的函数属性，通过把“数列—特殊函数”“等差数列—一次函数”“等比数列—指数函数”联系起来，引导学生感受数列与函数的联系与区别.此外，新版教材多次使用猜想或迭代等不完全归纳法，并将数学归纳法作为选学内容补充在数列这一章的最后一节，与前述知识方法形成了一个思维整体，有助于学生构建逻辑严密连贯的方法体系.

（2）例习题编排

从例习题的编排结构来看，旧版教材以“小节”为编排单位，按照“例题—练习—习题”的顺序编排，新版教材以“课时—小节”为编排单位，按照“课时（例题、练习）—小节（习题）”的顺序编排. 新版教材更加注重知识系统与训练系统的有机融合，与教学内容的适配性更佳.

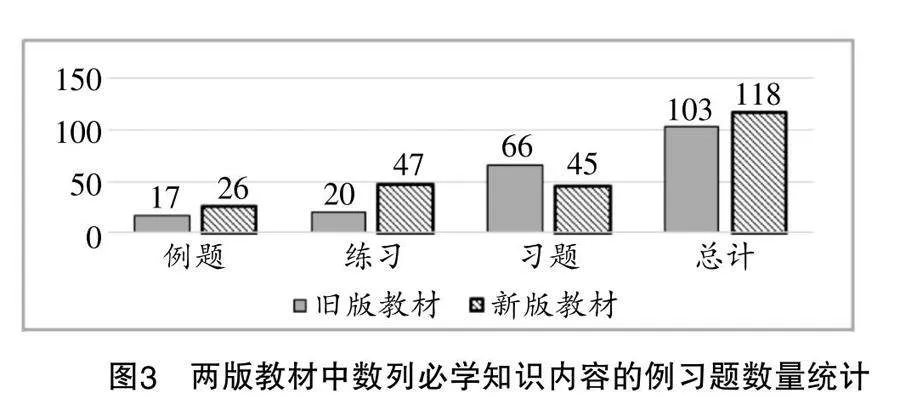
从例习题的数量来看（统计结果如图3所示），新版教材大幅增加了例题、练习，减少了习题，删减了旧版教材中的52道例习题，保留了32道，改编了19道（有4道题目合并成了2道题目），新增了69道，例习题的调整数量高达72.8%. 具体地，新版教材增加了证明题、探究题，适度关注训练系统与高考的关联，提高了应用题的质量. 在旧版教材中，有4道例题所涉及的知识点单一，可直接套用公式求解；在新版教材中，有6道例题涉及“等差×等比”型数列、“等差-等比”型数列、数列构造等，更好地体现了数列模型应用的丰富性与层次性.

从例习题层次来看，新版教材将旧版教材中的“A组”“B组”两个层次的例习题调整为“复习巩固”“综合运用”“拓广探索”三个层次. 本文应用SOLO分类理论［3］对例习题思维水平进行了统计分析，结果如图4所示. 在两版教材中，例习题思维水平层次分布总体相似，单点结构的例习题比例和拓展抽象结构的例习题比例相近，分别约为20%和9%. 在新版教材中，多点结构的例习题比例约为47%，较之前下降了6%；而关联结构的例习题比例约为24%，较之前增加了6%. 新版教材增加了关联结构的例习题比例，使得不同思维水平的例习题分布更为均衡，有效地促进了教学的循序渐进. 多层次的例习题设计，为不同数学基础和思维层次的学生提供了适宜的学习材料，有助于实现因材施教.

图4 两版教材中数列必学知识内容的

例习题思维水平统计

研究启示

通过对两版教材数列知识内容的比较分析，新版教材充分体现了培养数学学科核心素养的特点.研究发现：（1）新版教材注重数学知识的整体建构，突出对研究数学对象基本套路的呈现，按照“背景—概念（定义、表示、分类）—性质—特例（等差数列、等比数列）”编排章节内容，强调数列的函数属性，借助图表的直观作用，促进对数列本质的理解；新版教材以“运算”作为一般观念贯穿数列整章知识编排，引导学生从“运算”的视角来研究数列，深化对数与数量关系基础研究方法的理解.通过从不同角度整体理解数学知识，促进数学思维素养的发展［4］24. （2）新版教材注重知识系统与训练系统的整体设计.知识层面，注重生成过程，借助“思考”“探究”“归纳”“旁注”等栏目，构建问题链，加强教材对学习的引导功能，帮助学生掌握归纳、抽象、类比、推理等数学思想方法，积累活动经验；训练层面，注重知识与训练的统一，优化编写逻辑，合理设计例习题的比例和各思维水平层次的例习题的比例，引导教学循序渐进. 通过两个系统的有机融合，促进数学方法素养的提高［4］24. （3）新版教材注重问题情境的全面丰富，创设了多种类型和层次的学习情境，精选了富有时代气息的问题情境.通过熟悉的情境，帮助学生理解较为抽象的概念、性质等；借助关联的数学情境、科学情境、人文情境等，引导学生感悟数学的科学价值、文化价值、审美价值；依托综合的实际情境，引导学生应用数学知识解决实际问题. 通过运用数学知识和方法解决各类问题，促进数学工具素养的提升［4］24.

1. 注重“四基”，构建知识结构体系

“四基”是培养学生数学学科核心素养的有效载体. “四基”教学要注重知识的上、下位联系，关注结构性，突出整体性. 教学应立足教材编写的主线，从教材结构入手，整体把握数学教学内容之间的内在联系，克服仅关注基础知识、基本技能的教学局限，树立单元整体教学意识. 通过单元教学整合“碎片化”的知识，引导学生把握数学知识的本质，明晰数学知识之间的联系与区别，促进学生形成良好的认知结构. 例如，数列章节的概念教学要紧扣数列与函数的联系，深化项与序号之间的函数关系，理解给定一个序号就有一个确定的数与之对应的数列本质，理解通项公式是函数，前n项和公式也是函数；在教学等差数列与等比数列时，应充分利用它们知识结构的相似性，将“差”变为“商”，引导学生积累并应用数学活动经验.

2. 发展“四能”，内化数学研究方法

“四能”是发展学生数学学科核心素养的重要途径. “四能”教学要以问题为导向，以数学活动为载体，关注情境性，突出过程性.教学应深入理解教材的编写意图，厘清教材中相关内容、素材、例习题之间的关系，多思考教材中的数学问题是如何发现和提出的，明晰数学研究方法，引导学生经历发现、提出、分析、解决问题的学习全过程. 例如，在教学通项公式与求和公式时，要注意数列与函数的区别：函数的研究内容是对应关系、图象和性质，强调运用数形结合思想研究问题；数列的研究内容是通项公式和求和公式，强调运用数学运算研究问题. 在教学时，要重视列举、观察、归纳，强化合情推理. 对于教材中“研究数列｛ａ｝，｛ｂ｝的公共项，以及数列｛ａ±ｂ｝，｛ａ·ｂ｝，”等情境，教学时要引导学生从运算的观点出发，发现并提出新的数列问题. 此外，很多数列问题的分析和解决，离不开数学归纳法的演绎推理，建议面对学情较好的学生，将数学归纳法调整为必学内容.

3. 强化“三会”，提升数学核心素养

“三会”是提升学生数学学科核心素养的行为表现. “三会”教学要“以生为本”，以“三会”等行为表现为目标，关注创新性，突出实践性.教师应多读、多思，舍弃应试教育教学的功利取向，深层次把握知识本质，增强学生数学内部的“三会”表现；多创设好的实际问题，提高学生数学外部的“三会”表现. 例如，从数学内部来看，等差数列的性质与平均数紧密相连，等差中项是平均数的特例，等差数列的前n项和也可以从平均数的角度进行阐释；等比数列的性质与比例的性质紧密相连，等比中项是比例的特例，等比数列的前n项和也可以从比例性质的角度进行研究. 从数学外部来看，教材提供了“垛积术”“隙积术”“圭垛数”等数学文化素材，以及“理财产品”“贷款”等贴近生活的实际问题. 在教学中，不仅要充分利用这些素材来培养学生运用数学知识解决实际问题的能力，还要发挥其文化价值和应用价值，以此来培养学生的综合素养.

4. 变革方法，切实促进学生发展

从”四基”“四能”到“三会”是一条培养学生数学学科核心素养的主线.教学不妨紧扣这一主线，以单元整体教学变革教学方法，促进学生发展. 首先，从单元整体视角设计教学目标. 设计教学目标不仅要关注显性目标，还要关注隐性目标. 不妨从“四基”“四能”“素养”三个层面进行目标设计，既关注学生“学会”，又关注学生“会学”. 其次，将研究方法作为单元教学主题. 数列知识内容的教学，可以把“运算”作为教学明线，把基本套路作为教学暗线，以知识为学习载体，帮助学生掌握研究数学对象的一般方法，把握知识间的内在联系. 再次，按“一般对象—特殊对象”的教材编写逻辑设计学习顺序. 先按照研究方法学习一般数列，再通过类比学习特殊数列，从而感悟研究方法，深化类比思想，促进迁移能力的培养. 最后，通过总结归纳，完善学生的认知结构. 通过连接知识间的关联点，将新知识融入现有的认知框架，进行重塑或改造，从而构建一个逻辑严密、连贯且结构功能完善的知识体系.

参考文献：

［1］ 张定强，梁会芳，杨怡. 数学学科核心素养导向的“三角函数”教材内容变革［J］. 数学通报，2021，60（12）：4-7.

［2］ 章建跃. 通过代数运算研究数列建立数列模型解决问题［J］. 数学通报，2021，60（9）：4-11+19.

［3］ 于涛，薛新建. 基于SOLO分类理论的高考函数与导数模块研究：以全国Ⅰ卷（理科）和新高考卷为例［J］. 数学通报，2022，61（5）：46-51.

［4］ 宁锐，李昌勇，罗宗绪. 数学学科核心素养的结构及其教学意义［J］. 数学教育学报，2019，28（2）：24-29.