我国制造业资本劳动替代弹性和技术进步偏向

关键词：资本劳动替代弹性；技术进步方向；微观数据；宏观加总

DOI：10.19313/j.cnki.cn10-1223/f.20241017.002

一、前言

在常数替代弹性（CES）生产函数的框架下，替代弹性刻画资产和劳动相对价格发生变化时资产和劳动投入的相对变化，是决定要素份额如何随着要素价格变化而变化的关键因素（Hicks，1932）。替代弹性的大小与生产率有关 （ Klump 和 Preissler，2000），与经济增长有关（De La Grandville，1989），与技术进步方向有关（Acemoglu，2003）。特别是在研究劳动份额的分析中替代弹性的估计起到关键性作用（Karabarbounis 和Neiman，2014），当资本劳动的替代弹性大于1 时，劳动相对于资本价格的上升会导致劳动份额的下降；而当弹性小于1时，增加的资本积累或者资本相对于劳动价格的下降会导致劳动份额上升；弹性等于1 时劳动收入份额不变。弹性大于1，资本和劳动是富有弹性的，两者是替代品；如果弹性小于1，资本和劳动是缺乏弹性的，两者是互补品（Acemoglu，2002）。因此，替代弹性是刻画生产函数和技术进步偏向性的重要参数，对于相关的政策分析起到关键性作用（León-Ledesma 等，2010）。

资本劳动替代弹性在理论上非常重要，但是对弹性大小进行估计存在困难，其中之一是难以同时识别CES 生产函数中的替代弹性和技术进步（Oberfield 和Raval，2021）。Diamond 等（1978）证明了不可能定理，指出识别替代弹性和技术进步的前提条件是要素价格变动与技术进步方向是相互独立的，除非已经知道替代弹性的大小，否则技术进步方向是难以检测的。为了解决替代弹性和技术进步相关性的问题，文献中通常对技术进步的变化形式进行设定，通常假设要素技术进步是时间变量的函数，但这样做并不能得到真实的弹性，也没有解决要素价格变动与技术进步偏向之间的相关性问题（León-Ledesma 等，2010；Grossman 和Oberfield，2022）。目前国内外对弹性大小进行测算的文献没有得出一致的结论，不同研究者使用相同或者不同的数据以及不同的方法得到的结论有很大的差异，对于中国资本劳动替代弹性测算的结果大致在0.5-2.0之间。

近年来有文献应用微观企业的截面数据对弹性进行估计，在考虑异质性和要素配置的情况下对微观弹性进行加总，得到行业或者部门的总体弹性（Raval，2019；Oberfield 和Raval，2021）。这种估计方法有几点好处：一是不需要事先对技术进步的方向和速度进行假设；二是能够对不同年份的弹性分别进行测算，进而分析替代弹性是否具有时间常数性或者如何随时间变化；三是企业层面的数据提供了丰富的关于资本强度、规模等异质性的信息，而这些异质性信息可以用来测算加总的弹性，并有助于进一步分析异质性和资源配置对总量弹性的影响。

本文的主要内容是基于 Oberfield 和Raval（2021）和Raval（2019）提出的理论框架，运用中国工业企业数据库以及企业所处地级市行业平均工资的截面数据，首先对制造业28 个行业的局部资本劳动替代弹性进行估计，然后运用从微观到宏观加总的方法，在考虑企业和行业资本强度异质性的情况下，将行业局部替代弹性逐步加总为行业整体替代弹性以及制造业总体替代弹性，在此基础上识别出行业和制造业的技术进步方向，并进一步对要素投入相对价格和技术进步偏向的变化对制造业劳动收入份额变化的作用进行了分解，对影响未来制造业劳动收入份额变化趋势的因素进行了分析。

本文研究主要有以下几点发现：一是我国28个制造业行业的资本劳动替代弹性的差异性较大，在0.5-1.5之间；二是制造业部门的替代弹性呈现下降的趋势，从1998～2001年的1.13下降到2002～2007年的1.06，以及2011～2013年的0.88；三是技术进步方向为资本增强型；四是用测算得到的替代弹性和技术进步方向能较好地解释近20 年来制造业劳动收入份额的变化，并指出技术进步偏向是导致制造业劳动收入份额变化的主要因素；五是利用实证分析的结果对未来制造业劳动收入份额的变化趋势进行了分析，指出未来要素价格变动和偏向性技术进步对劳动收入份额的影响是相反的，要素价格变动对劳动收入份额变动的影响为正，偏向性技术进步的影响大概率为负，劳动收入份额的变化由两者的相对大小决定；六是将替代弹性从来源方进行分解，发现企业的异质性明显扩大了行业局部替代弹性（局部和整体行业替代弹性的概念在后文解释），但扩大效应在样本后期有所减弱。行业之间由于异质性而导致的资源配置效应对制造业部门弹性的扩大效果比较微小。

本文可能的边际贡献有以下几点：一是尝试运用微观企业数据并考虑企业异质性和资源配置效应这一较新的研究方法对我国制造业以及其中28个行业的替代弹性进行了估算，并得出我国制造业替代弹性呈现下降趋势的结论，类似的从微观到宏观的加总方法也可以用于对我国总体替代弹性的估计；二是对引起替代弹性变化的因素进行了分解，对劳动收入份额变化的原因进行了分析；三是从替代弹性与劳动收入份额关系的角度对未来我国制造业劳动收入份额的变化趋势进行了分析和判断。

本文结构如下：第一部分为前言，第二部分为文献综述，对现有文献中有关资本劳动替代弹性的估计方法以及结果进行回顾与总结；第三部分介绍Oberfield 和Rava（l 2021）以及Rava（l 2019）提出的理论框架，以及本文的估计方法；第四部分运用我国工业企业数据对我国28个制造业行业和制造业部门的替代弹性进行测算；第五部分讨论实证分析中的内生性和估计的稳健性；第六部分是结论和总结。

二、文献综述

Diamond等（1978）指出替代弹性不能从产出、投入和边际产出的时间序列中得到识别，识别需要满足要素价格的变动与技术进步偏向相互独立的条件。在对弹性进行估计时，为了满足识别条件，一些文献在生产函数中对技术进步的形式施加约束，比较常用的方法是假设技术进步是无偏的，或者假定要素技术进步偏向是时间变量的函数，增长率是常数或者随时间变化（Antras，2004；Klump等，2007）。在估计方法方面，较早的文献或者用多项式方法将非线性CES生产函数通过泰勒多项式展开为线性表达式（Kmenta，1967），或者基于一阶条件的单方程，用OLS、IV等方法对一阶条件组成的系统进行估计，或者使用非线性估计方法直接对CES生产函数进行估计。Klump 等（2007）以及 León-Ledesma等（2010）提出了标准化供给面系统模型方法，基于CES生产函数和一阶条件组成的方程系统对CES 生产函数进行估计，通过蒙特卡洛实验证明，这一系统方法比单方程估计方法、线性近似方法以及非线性方法等常用的方法有更好的估计效果，之后在CES 生产函数的估计中被广泛使用。

在使用标准化供给面系统模型方法对中国的替代弹性进行估计的文献中，一些文献得到的结果是弹性大于1（陈登科和陈诗一，2018；Manu 等，2022），另一些文献估计的结果是弹性小于1（戴天仕和徐现祥，2010；陆雪琴和章上峰，2013；罗楚亮和倪青山，2016；郝枫，2017）。Manu等（2022）使用供给面系统方法和中国时间序列数据进行估计，假设技术进步是时间可变，样本为1978～2017年，估计结果是1.308。陈登科和陈诗一（2018）运用1998～2007年的中国工业企业数据，使用面板模型，对31个两位数制造业分行业的替代弹性进行估计，替代弹性均明显大于1，基本在1.7-2.1之间。戴天仕和徐现祥（2010）运用正规化供给面系统估计方法，使用1978～2005年中国时间序列数据，估计出我国的替代弹性是0.74；郝枫（2017）利用1978～2014年省份面板数据估计中国替代弹性和技术偏向，结论是我国三次产业替代弹性均小于1；陆雪琴和章上峰（2013）使用León-Ledesma（2010）以及Kmenta（1967）的泰勒展开方法，基于中国1978～2011年时间序列数据估算了CES 生产函数中的参数，估算出的结果为替代弹性为0.78；罗楚亮和倪青山（2016）基于中国工业企业数据对1999～2007年每年的替代弹性进行单方程回归估计，结果在0.65-0.75之间。柏培文和王亚文（2023）估计分行业资本替代弹性，考虑不同技能劳动与资本的替代弹性以及技术进步偏向，对我国31个行业以及第一、二、三产业1995～2014年的资本与高、中、低技能的替代弹性分3个阶段分别进行估计，得到结论是资本和高技能劳动之间替代弹性小于1，是互补关系，与中低技能之间的弹性大于1，是替代关系。

在使用微观数据进行估计时，Houthakker（1955）证明总量的弹性不等于微观弹性，在加总时取决于微观企业异质性的分布。Raval（2019）提出应用截面企业调查数据估计局部产业替代弹性的方法。Oberfield和Raval（2021）提出将局部产业替代弹性加总为产业整体替代弹性和制造业部门总弹性的方法，即加总的弹性是企业层面弹性和需求弹性的线性组合，权重与企业在行业中资本份额的分布有关。运用此方法，不需要对技术进步偏向随时间的变化做出事先假设和限制，而且技术进步偏向和要素价格的变动是相互独立的，使用截面数据还可以估算替代弹性和技术进步偏向随时间变化的情况。

本文首先在Raval（2019）的理论框架下运用中国工业企业数据测算中国制造业28个行业的局部弹性，然后在Oberfield和Raval（2021）的理论框架下估计产业的整体弹性和制造业部门加总的弹性，在此基础上识别出技术进步方向，并对劳动收入份额变化的来源进行分解，对其未来走势进行分析和判断。

沈春苗和郑江淮（2022）同样使用Raval（2019）、Oberfield和Raval（2021）的分析框架，使用中国工业企业数据对我国制造业行业和部门的替代弹性进行了估计。本文在具体数据处理方法和估计方法方面与沈春苗和郑江淮（2022）有所差别，得到的估算结果不完全相同，相同之处是在2011年之后的弹性小于1，不同之处是本文的测算结果显示制造业部门的替代弹性在2007年之前大于1，即资本与劳动是相互替代的。

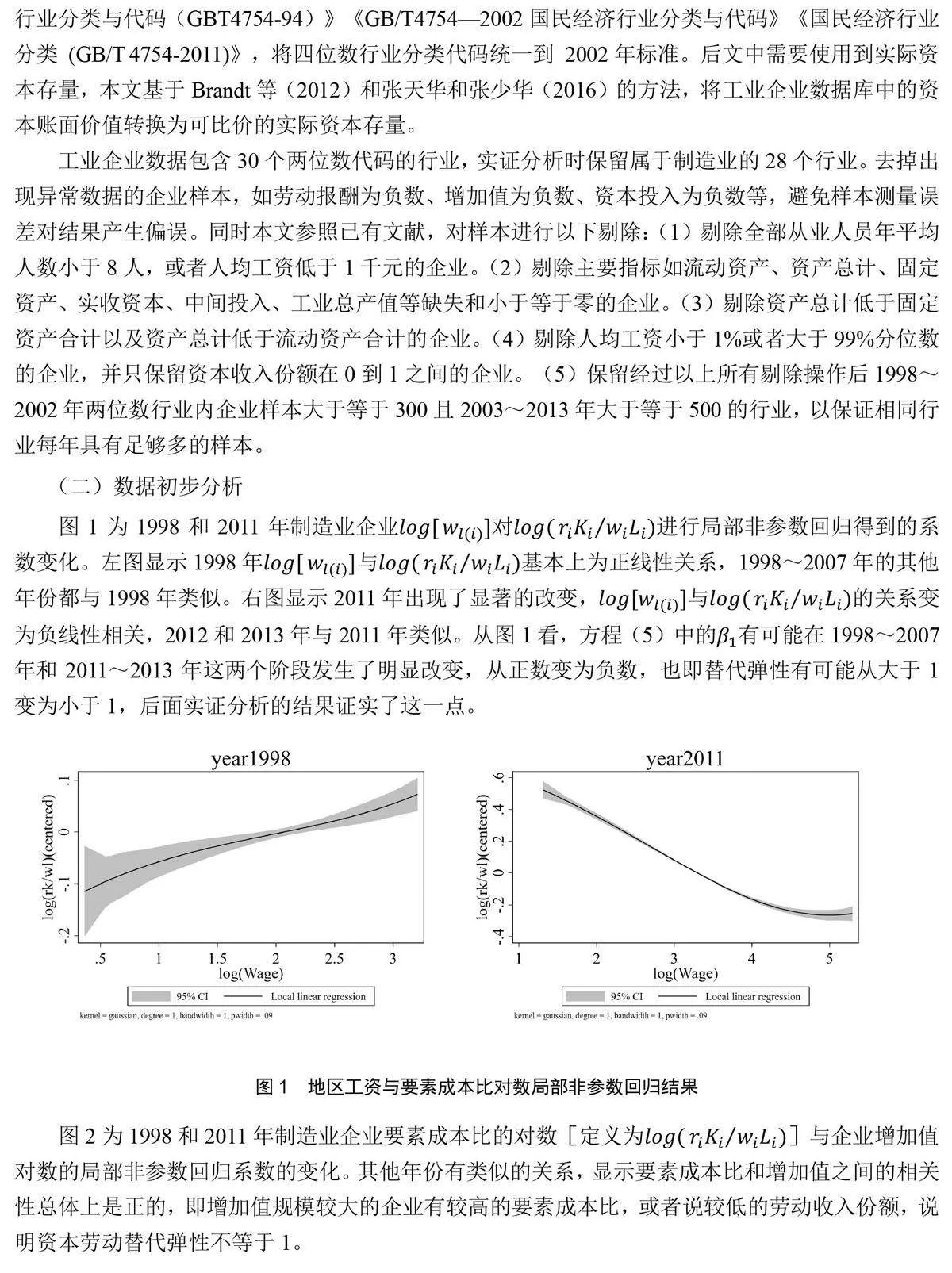
后续实证分析中需要分行业计算，因此需要统一四位数行业的划分标准。本文参照《国民经济行业分类与代码（GBT4754-94）》《GB/T4754—2002国民经济行业分类与代码》《国民经济行业分类 （GB/T 4754-2011）》，将四位数行业分类代码统一到 2002年标准。后文中需要使用到实际资本存量，本文基于Brandt 等（2012）和张天华和张少华（2016）的方法，将工业企业数据库中的资本账面价值转换为可比价的实际资本存量。

工业企业数据包含30个两位数代码的行业，实证分析时保留属于制造业的28个行业。去掉出现异常数据的企业样本，如劳动报酬为负数、增加值为负数、资本投入为负数等，避免样本测量误差对结果产生偏误。同时本文参照已有文献，对样本进行以下剔除：（1）剔除全部从业人员年平均人数小于8人，或者人均工资低于1千元的企业。（2）剔除主要指标如流动资产、资产总计、固定资产、实收资本、中间投入、工业总产值等缺失和小于等于零的企业。（3）剔除资产总计低于固定资产合计以及资产总计低于流动资产合计的企业。（4）剔除人均工资小于1%或者大于99%分位数的企业，并只保留资本收入份额在0到1之间的企业。（5）保留经过以上所有剔除操作后1998～2002年两位数行业内企业样本大于等于300且2003～2013年大于等于500的行业，以保证相同行业每年具有足够多的样本。

（三）对σ、ε、ζ、σ^agg的估计

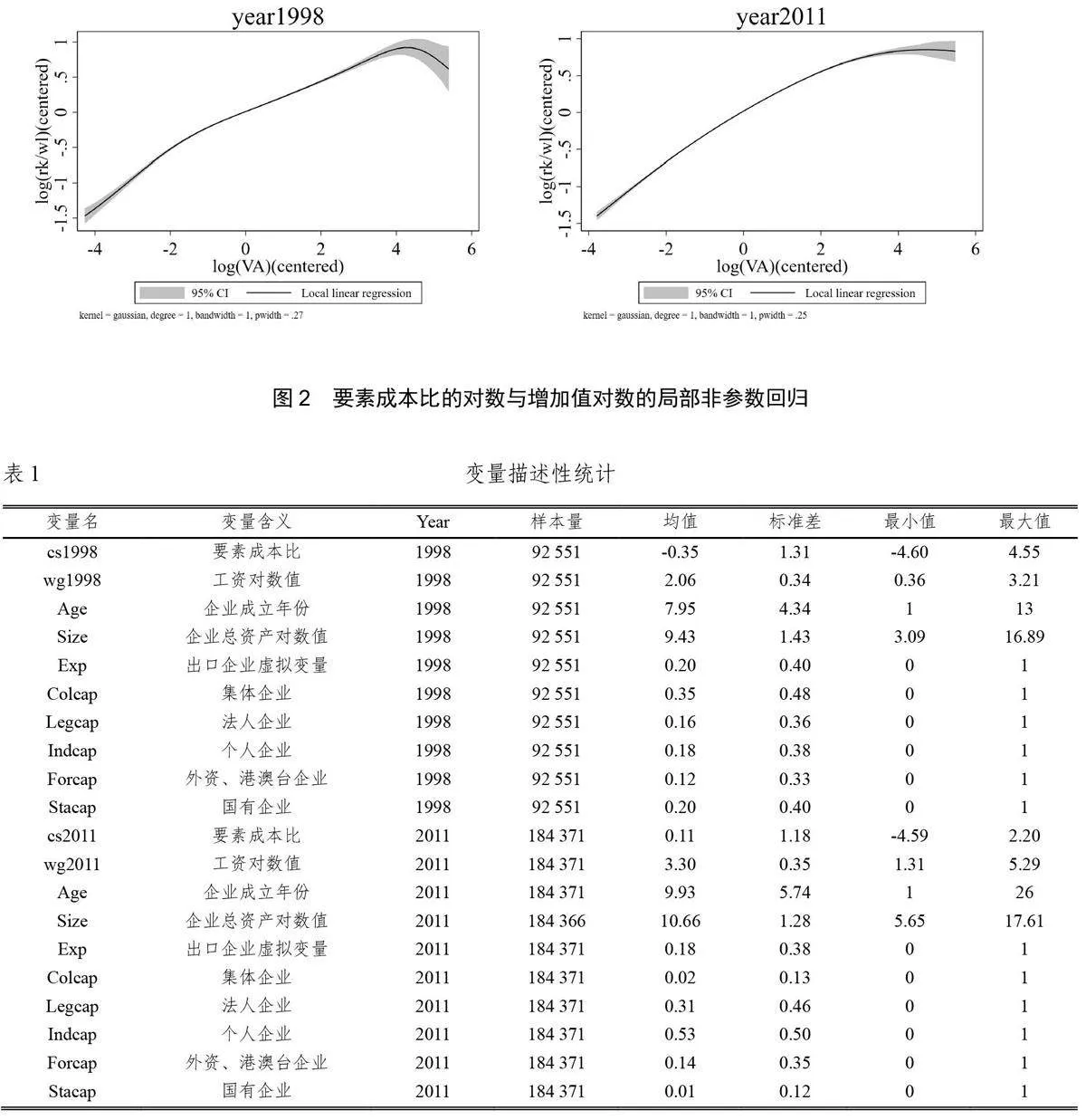
方程（5）中的控制变量为企业所属省份的哑变量prov、企业年龄age、企业规模size、企业类型虚拟变量、企业出口虚拟变量。企业规模size由企业资产总额的对数值代理；企业类型虚拟变量的定义为，根据企业实收资本中所占比例最高来源，将企业类型划分为国有企业、外资企业（含港澳台）、集体企业、民营企业和法人企业等五类；企业出口虚拟变量的定义为，若企业出口交货值占工业销售产值大于20%，则视为出口型企业，出口虚拟变量等于1，否则视为非出口型企业，出口虚拟变量等于0。表1 对数据定义和统计性质（1998和2011年）进行了描述。

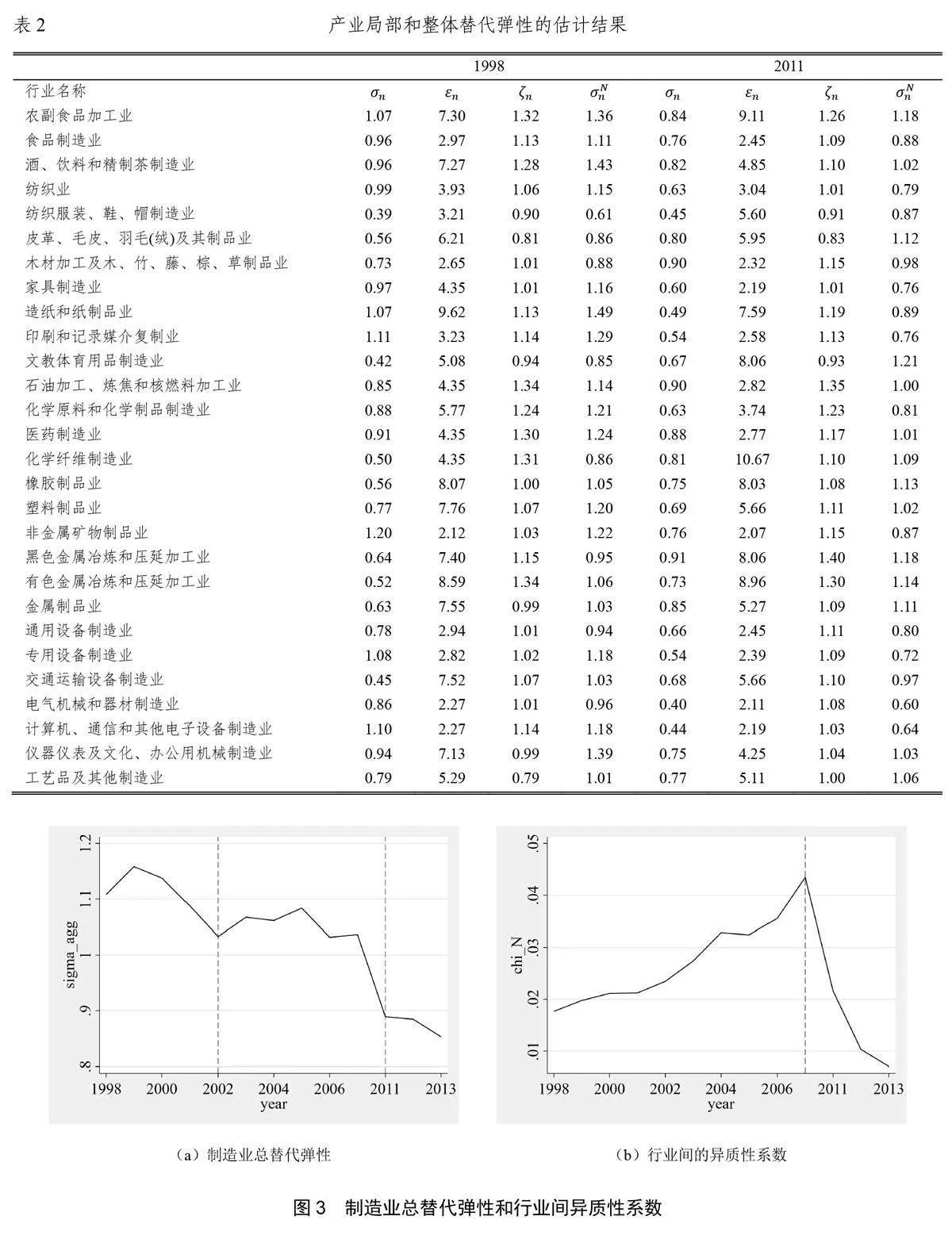
用1997～2007年以及2011～2013年每一年分行业企业的截面数据以及OLS对方程（5）和（6）进行估计，得到28个行业局部弹性的估计结果，在表2 中给出（1998 和2011年）①。

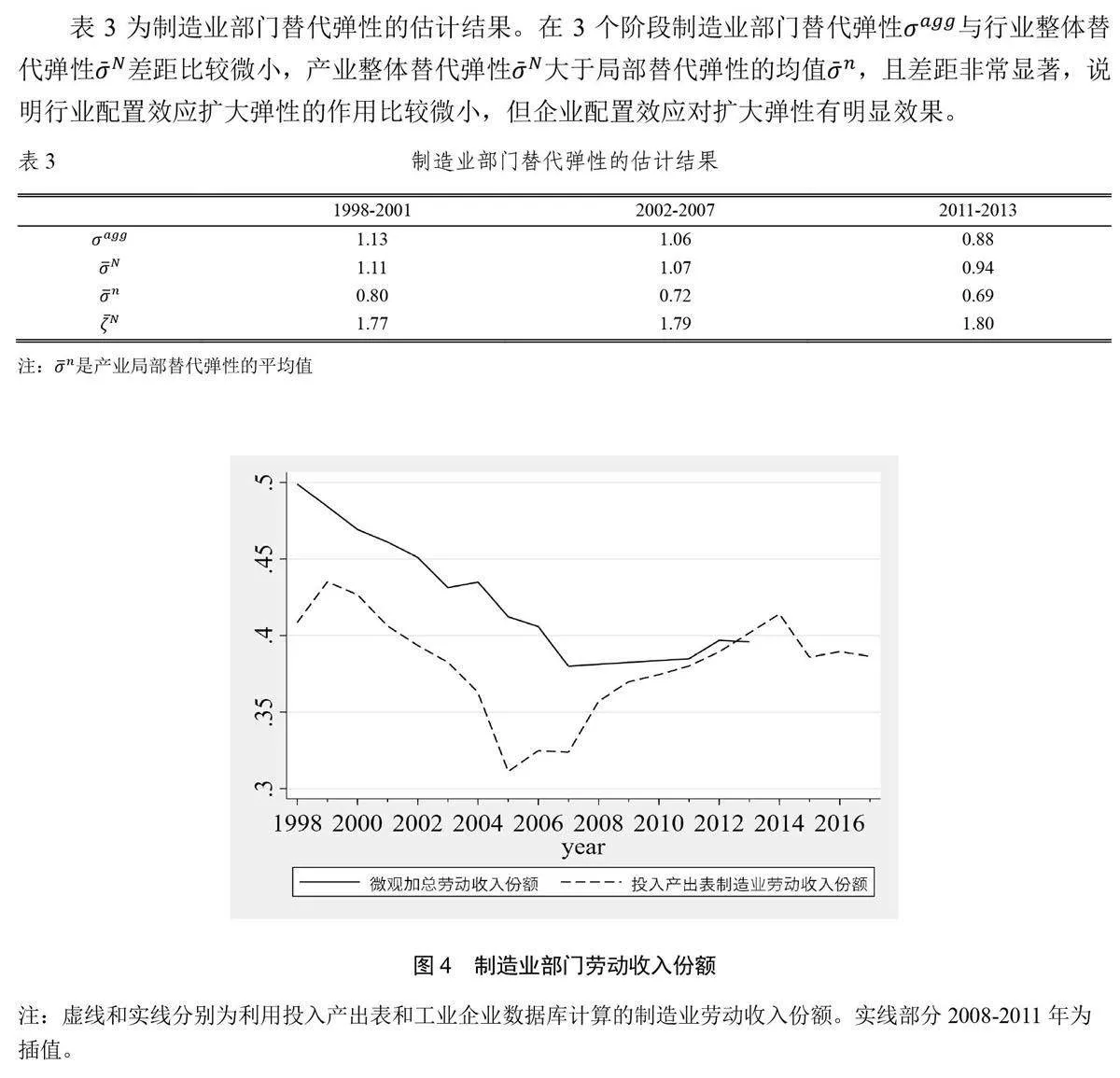
图3（a）和（b）分别为制造业部门替代弹性σ^agg，以及相应的行业间异质性系数X^N的变化。σ^agg呈现持续下降的趋势，在2003～2007年这个时间段内相对比较稳定。X^N在1998～2007 年呈现持续上升的趋势，2011～2013年比2007年明显下降。

（四）劳动收入份额的分解

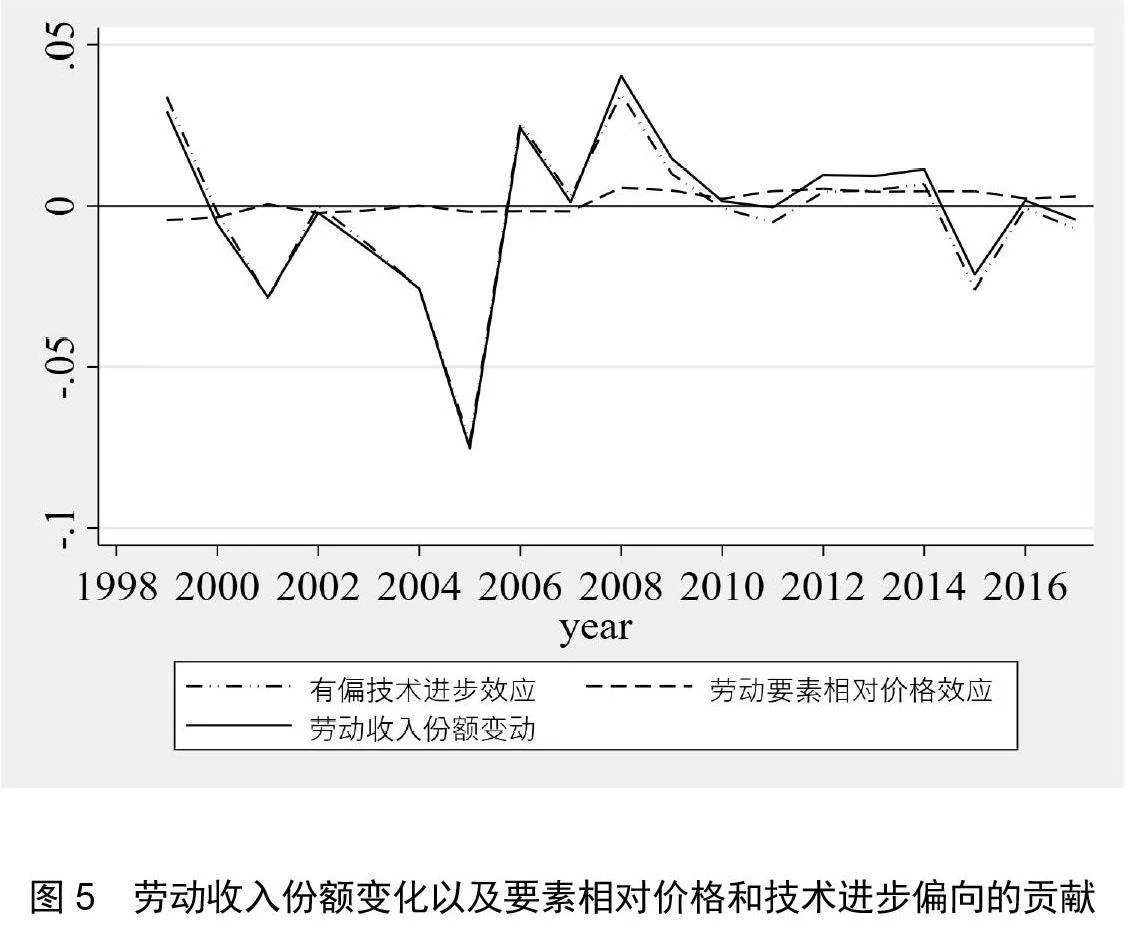
首先利用投入产出表计算制造业宏观劳动收入份额，对于数据缺失年份利用线性插值法补齐（图4 中虚线），同时利用工业企业数据库微观企业加总的数据计算微观劳动收入份额（图4 中实线）。图4显示，两者的变化趋势基本一致，即在过去近20年我国劳动收入份额经历了1998～2007年的快速下降、2008～2014年快速上升，以及2015～2017年保持平稳的3个阶段。

大量文献表明，替代弹性对于劳动收入份额变动具有重要意义（Grossman 和 Oberfield， 2022；汤灿晴和董志强，2017），大部分文献中假设资本劳动替代弹性是固定不变的参数，但是根据本文的测算，资本劳动替代弹性随时间发生了明显变化，从大于1逐渐下降到小于1，资本和劳动从替代关系逐步转变为互补关系，这种替代关系的变动，对于解释劳动收入份额变动的来源具有重要影响。参考Oberfield 和Raval（2021）关于劳动收入份额的分解方法，本文运用前文估计的制造业总替代弹性σ^agg对1998～2007、2011～2017年的劳动收入份额进行分解，其中2014～2017年使用σ^agg在2011～2013 年估计的平均值，劳动份额和要素价格使用制造业的宏观数据。

图5显示有偏技术进步变化是影响劳动收入份额变化的主要因素，但随着资本劳动替代弹性逐渐降低，劳动要素价格的相对上涨对于宏观劳动收入份额上升开始具有推动作用。

（五）对实证结果的进一步讨论

本文采用从不同行业层面的资本劳动弹性出发，逐步加总到产业层面以及宏观层面的弹性的测算方法，对28个制造业行业的替代弹性分别进行估计，发现行业之间存在较明显的差异性。我国正处于产业结构不断调整和升级的过程中，得到的不同产业和行业的替代弹性能够为判断未来产业结构调整所引起的替代弹性变化趋势提供有用信息。

本文的一个重要结论是我国制造业替代弹性在1998～2013年之间呈现下降趋势，而且目前替代弹性小于1（假设弹性在2013年之后没有明显变化），这一发现与德拉格兰德维尔假说 （De LaGrandville，1989）是基本一致的，即资本劳动替代弹性越大，经济增长率越高。在这一时期，我国工业增加值增长速度出现下降趋势，从1993年的19.96%下降到2013年的7.73%以及2023年的4.20%。替代弹性小于1 的结论能够为分析我国技术进步方向以及未来我国制造业劳动收入份额的变化趋势提供有用信息。用测算得到的替代弹性和技术进步方向能较好地解释近20年来制造业劳动收入份额的变化，并指出技术进步偏向是导致制造业劳动收入份额下降的主要因素，对分析我国收入不均等的走势具有一定的政策参考价值。

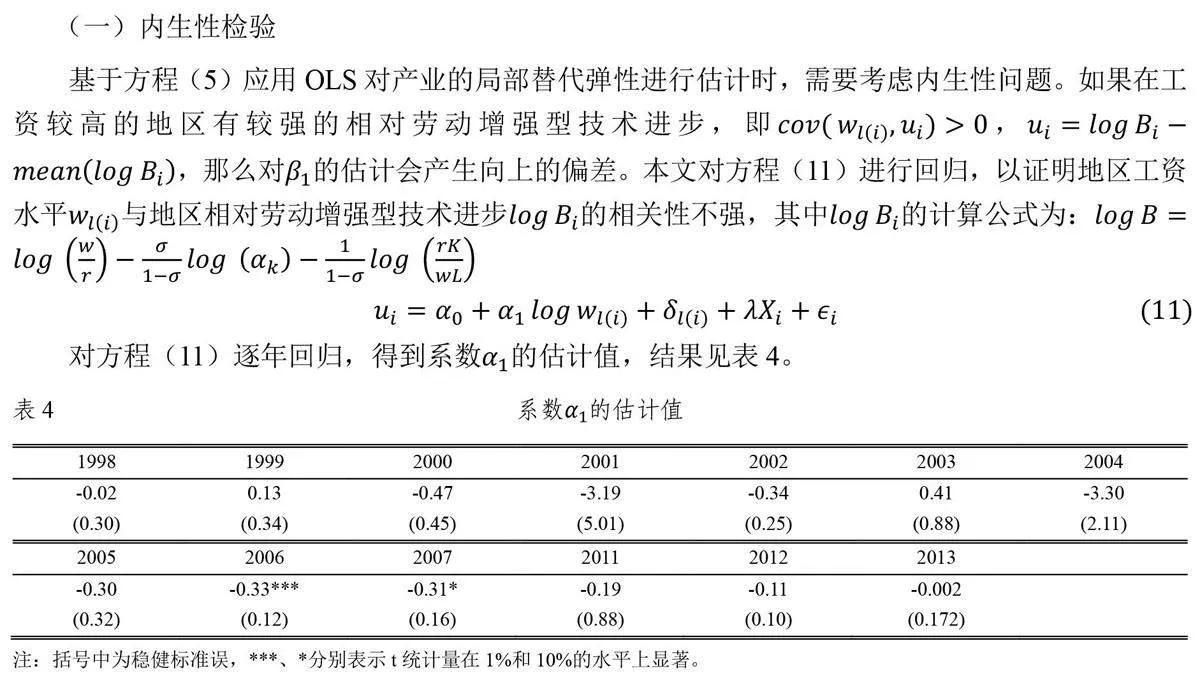
五、内生性和稳健性检验

从表4可知，除2006和2007这两年外，其他绝大多数年份中没有发现在工资较高的地区有较强的相对劳动增强型技术进步，也就是说本文的估计结果不存在明显的偏误。

（二）稳健性检验

为了检验基准模型的稳健性，这里设计了3个稳健性检验。一是使用地级市的平均工资替换基准模型中企业的平均工资。二是采用生产法增加值替换基准模型中的企业增加值，生产法增加值的定义为企业增加值=总产出-中间投入，变量缺失年份参考朱沛华和陈林（2020）的方法补全，即中间投入=总产值*主营业务成本/主营业务收入-应付工资总额-当年折旧+财务费用。三是在解释变量中加入了企业资本回报率。在估计方程（5）时需要考虑的一个问题是企业资本回报率不同会导致估计系数有偏，有些文献利用工具变量等方法解决该问题，但是考虑到工具变量本身估计效率较低，且存在局部平均处理效应等问题，本文测算了企业资本回报率，将其加入方程（5）的解释变量中，直接解决了资本回报率不同导致的估计系数有偏问题。表5 比较了基准模型与3 种稳健性检验的弹性估计值，发现在各种模型设定下结论基本稳定，即在2007 年以前制造业部门替代弹性基本大于或等于1，在2007年后弹性小于1，且均呈现下降趋势。

六、结论和总结

本文实证结果表明，制造业部门的资本劳动替代弹性具有较为明显的下降趋势，在2007年后资本劳动要素替代弹性小于1，这是分析我国劳动收入份额变动时需要考虑的重要问题。

在很多使用时间序列或者面板模型对替代弹性进行估计的文献中，通常假设弹性是不随时间变化的常数，但是从本文的估计结果看，在过去近20年，我国制造业部门的替代弹性有可能发生了趋势性变化，从1998～2002年的1.13下降到2011～2013年的0.88，目前保持较稳定的状态。Oberfield 和Raval（2021）使用相同方法测算其他国家制造业部门的替代弹性，美国、印度、智利分别为0.74、1.2、0.85，也就是说我国制造业弹性高于美国，低于印度，与智利接近。2007～2013年我国资本劳动替代弹性由大于1逐渐下降到小于1，同时，工资率相对于资本使用成本出现上升，在这种情形下2011年之后要素价格的相对变动推动了劳动收入份额上升，同时2007～2013年技术进步的方向是资本增强型，也对劳动收入份额的上升起到推动作用。

假定未来替代弹性仍然小于1，即资本和劳动是互补的，那么未来要素价格变化很可能会继续推动劳动收入份额上升。技术进步方向对劳动收入份额变化的影响不确定，如果技术进步的方向是资本增强型的，那么与要素价格变动的作用方向是一致的，两者都会导致收入份额继续上升；如果技术进步方向是劳动增强型的，会推动劳动收入份额下降，劳动收入份额的变化方向取决于两者贡献的大小。技术进步的方向可能受到两种效应的影响（Acemoglu，2002），一是稀缺要素得到更多的研发投资而改善稀缺要素的生产率，其效果是提高稀缺要素的生产率；二是市场规模效应有利于资源向富裕的要素配置，其效果是提高富裕要素的生产率。未来存在许多影响技术进步方向的潜在因素，特别是数字经济、人工智能、机器人等新技术的发展和应用，将对未来技术进步方向和劳动收入份额变化产生重要影响，也是未来需要进一步研究的主题。