基于贝叶斯网络的道路交通事故致因路径分析

摘要：为了分析道路交通事故的发展过程和演变规律，以云南省某司法鉴定中心收录的2010—2023年间云南省各州、市道路交通事故调查数据库为基础，结合国家车辆事故深度调查体系（NAIS）中对于道路交通事故调查的关键信息记录项，提取出包含时间、道路、人员等4类因素在内的17个致因项，构造事故致因分析数据集。其次，利用基于评分函数的爬山算法对贝叶斯网络（BN）进行结构学习，结合专家经验确定贝叶斯网络的拓扑结构，利用最大似然估计的方法对BN进行参数学习，确定最终的事故致因贝叶斯网络。最后通过敏感性分析识别关键事故致因路径，利用通径模型分析路径的效应水平，确定最大致因路径。结果表明：道路因素是影响道路交通事故形态以及伤亡情况的主要因素，以这两类事故结果为末节点的关键事故致因路径分别有3条、4条，其中最大致因路径分别为“路面结构→道路类型→伤亡情况”“路面结构→道路类型→事故形态”。

关键词：交通安全；道路交通事故；贝叶斯网络；事故致因路径

中图分类号：U491.31 收稿日期：2024-10-24

DOI：10.19999/j.cnki.1004-0226.2024.12.021

1 前言

近年来，全国公安机关以道路交通事故预防“减量控大”工作为主线，全力做好防事故、保安全、保畅通各项工作，实现了全国道路交通事故稳中有降的目标。虽然事故数量有所下降，但每年仍有大量人员因道路交通事故而伤亡。例如，在应急管理部发布的数据中，2024年第一季度全国共发生事故3 570起、死亡3 359人，其中重特大事故4起、死亡82人。因此，对道路交通事故演化过程进行研究，对于降低道路交通安全风险具有重要意义。

当前对于道路交通事故的致因研究多是采用离散选择模型，如有序Probit/Logit模型[1]、混合Logit模型[2]等来分析各类致因对事故结果的影响程度。然而，这类模型往往局限于研究某些单一属性对事故结果的直接影响，缺乏对影响因素之间关联性的研究，即对事故致因路径进行研究[3]。而海因里希事故连锁理论[4]认为事故致因具有连锁效应，即可以通过消除事故路径中某个因素的方式来阻断事故的发生。

分析相关文献可知，此类研究与传统事故致因分析最大的不同之处在于它不再对某个事故致因进行独立分析，而是将它们视作相互关联的一个系统来研究。其主要的思路是先找到事故致因之间的内在逻辑性，然后通过建立树型或网络型结构对相关关系进行阐述，加之适当的数学模型处理，最后得到相应的事故链条，其中比较常见的结构模型有事故树模型[5]、事变树模型[6]、贝叶斯网模型[7]等。特别是贝叶斯网模型，其作为机器训练模型的一种，除了在事故预测方面的应用，也开始被用于对事故致因路径的挖掘[8]。

因此在利用相关事故数据集的基础上，引入贝叶斯网络模型对道路交通事故致因路径进行识别分析，可以为探究道路交通事故演化规律和制定相关事故的预防策略提供新的思路。

2 理论基础

2.1 贝叶斯定理

贝叶斯方法基于已经拥有的经验或者知识，用概率来衡量人们对某个事件真实度的相信程度。假设H是一个事件，K为试验之前已经拥有知识，那么p（H｜K）就是给定K以后关于H的概率或者对它的信仰。如果试验产生了一个数据D，那么就要将概率修正为p（H｜D∩K），这样的修正将包含在给定H发生或者不发生时关于数据的不确定性。在概率论中有三条正式的规则，由其可以推出任意的性质：

2.2 贝叶斯网络

贝叶斯网络（BN）属于概率图形（probabililistic grapical models，GM）族的一种网络模型，它以贝叶斯定理作为理论基础，涵盖了图理论、概率论、计算机科学及统计等领域的概念，主要的组成部分是一个有向无环图（directed acyclic graphic，DAG）结构（图1）。DAG的主要组成部分是节点（node）或顶点（vertex）以及有向边或者说是有向弧。无回路意味着没有节点是它自己的祖先或者后代，简单来说就是顺着网络中箭头的方向一直追溯不会经过已经走过的节点。

贝叶斯网络中的每个节点都对应着一个变量，可以给变量赋予不同的取值，箭头的方向表现了变量之间的依存关系。箭头指向的终点为“子节点”（child），起点称为“父节点”（parent）。和图模型类似，没有父节点的节点称为根节点（root node），没有子节点的节点为叶节点（leaf node），其他节点称为中间节点（intermediate node）。每个节点都附有给定其父节点的（条件）局部概率，因此贝叶斯网络也称为概率有向无回路图模型（probabilistic directed acyclic graphical model）。

3 事故致因贝叶斯网络构建

3.1 网络节点选择

构造贝叶斯网络的第一步是要确定网络节点，通过对相关事故数据库中的3291起道路交通事故的事故调查报告进行分析整理，结合国家车辆事故深度调查体系（NAIS）中对于道路交通事故调查的关键信息记录项[9]，提取出包括时间、车辆、道路等五个方面在内的17个事故参数项（表1），结合具体事故信息构造事故分析矩阵数据集（表2），以该数据集中的参数项及信息作为后续BN结构和参数学习的网络节点和训练数据集。

3.2 参数及结构学习

在多数情况下，BN的结构和条件概率表都是未知的，需要事先给出用于训练的数据集和先验信息（如专家知识和因果关系）来估计节点间的拓扑关系和贝叶斯网络中的联合概率分布，即结构学习（structured learning）和参数学习（parameter learning）。因此本文在matlab中采用基于评分函数的结构学习爬山算法来对BN进行结构学习，通过不断调整节点顺序和数量，得到以“事故形态”“伤亡情况”为末节点的初始拓扑结构。然后在初始结构的基础上结合专家经验对网络结构进行优化，剔除与末节点不相关的中间节点以及不合理的有向线段，得到最终的BN拓扑结构。

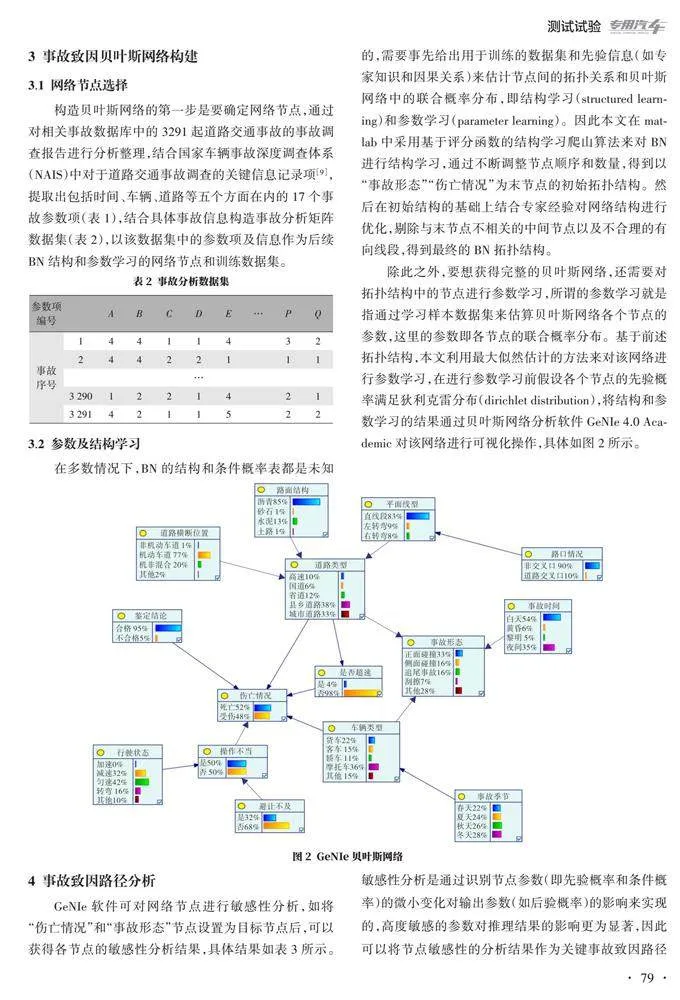
除此之外，要想获得完整的贝叶斯网络，还需要对拓扑结构中的节点进行参数学习，所谓的参数学习就是指通过学习样本数据集来估算贝叶斯网络各个节点的参数，这里的参数即各节点的联合概率分布。基于前述拓扑结构，本文利用最大似然估计的方法来对该网络进行参数学习，在进行参数学习前假设各个节点的先验概率满足狄利克雷分布（dirichlet distribution），将结构和参数学习的结果通过贝叶斯网络分析软件GeNIe 4.0 Academic对该网络进行可视化操作，具体如图2所示。

4 事故致因路径分析

GeNIe软件可对网络节点进行敏感性分析，如将“伤亡情况”和“事故形态”节点设置为目标节点后，可以获得各节点的敏感性分析结果，具体结果如表3所示。敏感性分析是通过识别节点参数（即先验概率和条件概率）的微小变化对输出参数（如后验概率）的影响来实现的，高度敏感的参数对推理结果的影响更为显著，因此可以将节点敏感性的分析结果作为关键事故致因路径识别的依据，其中敏感性分析的评价指标为敏感性指数Max值（记作MSI）。从敏感性分析的结果中筛选出MSI>0.01的中间节点及由这些节点组成的有向线段（具体如表3所示），由这些节点和线段可识别出不同类型事故的关键事故致因路径。从敏感性分析的结果来看，该网络中是否超速-K（0.031）对伤亡情况-O的影响最显著，事故时间-A（0.16）对事故形态-Q的影响最显著，道路横断位置-H、路面结构-E、道路类型-C是这两类目标节点的共同关键致因，道路因素是这两类事故结果的主要因素。

在敏感性分析的基础上对高敏感节点间的有向线段进行影响强度分析，以强度值作为影响强度的评价指标，强度值衡量的是该有向线段对整个链路的影响，由此可得到不同要素组合对路径影响权重。从分析的结果来看，在与伤亡情况有关的有向线段中“道路横断位置-H→道路类型-C”的联系最强（0.201），对事故链条的影响最显著，在与事故形态有关的有向线段中“事故时间-A→事故形态-Q”的联系最强（0.232），影响最显著。这些不同的因素组合可以作为事故预防中重点研究的对象，例如，县乡道路中的机非混合车道容易引发死亡事故，因此应在条件允许的情况下，通过设置护栏、绿化带等物理隔离设施，将机动车道与非机动车道明确分隔，减少机非混行的机会，从而降低事故风险；夜间行车由于视线受限和反应时间延长，更容易引发正面碰撞事故，应合理设置减速指示牌，引导驾驶员适当降低车速，在雨、雪、雾等恶劣天气条件下更是如此。

根据表3的网络分析结果识别出以伤亡情况和事故形态作为末节点的关键事故致因路径，在此基础上，对关键事故致因路径进行通径分析，得到各关键事故致因路径的通径系数，并通过统计分析检验路径的显著性，具体路径如图3所示。由图3可知，识别的关键事故致因路径分别有3条、4条，在与伤亡情况相关联的路径中，“路面结构→道路类型→伤亡情况”的效应水平（即路径通径系数乘积，该路径为0.018）最高，所以该路径为伤亡情况节点的最大事故致因路径；在与事故形态相关联的路径中，“路面结构→道路类型→事故形态”的效应水平最高（0.027），因此该路径为事故形态节点的最大事故致因路径。

在识别关键事故致因路径的基础上，可以通过改变路径中末节点状态概率的方式（如将事故路径中某个事件发生的概率设为100%）来向前推理得到剩余节点在整个事故路径中的更新传播结果，以此进一步分析事故路径的传播规律。例如，以图4中的事故路径为例，可以分析得到正面碰撞事故更容易在平面线型为直线段和右转弯的城市路段发生，侧面碰撞往往发生在县乡道路以及左转弯路段，超速的情况下更容易导致死亡事故等。根据类似的方式可以探究不同条件对各种类型事故的影响，进而为事故预防策略的制定提供有效参考。事故的发生是多个因素造成的，所以除了对重点致因进行防治，还可以从不同要素组合中得到启发，制定相关的预防策略。例如，针对事故多发的转弯路段增加提示性标志、在人员密集的城市道路及路况复杂的县乡道路进行有效划分，对人、车区域进行隔离等。

5 结语

本研究通过构造事故致因贝叶斯网络的方式分析了包括时间、道路等方面14个因素对道路交通事故结果的影响，利用敏感性分析的方法识别出不同类型事故的关键事故致因路径，并对致因路径进行了定量分析，最后通过改变节点状态的方式探讨了不同形成条件下的事故预防策略。具体结论如下：

a.从贝叶斯网络敏感性分析的结果来看，致因参数项中分别有5种、7种因素对事故的伤亡情况以及事故形态具有显著影响，道路因素是这两个末节点的共同主要致因，其中是否超速对事故伤亡情况影响最显著，事故发生的时间对事故形态的影响最显著。

b.利用通径模型分析tPfWtFTcWf3DrgTOvOytmHv/KSN2+vy9/q7pvmdElGk=得到的最大事故致因路径分别为“路面结构→道路类型→伤亡情况”“路面结构→道路类型→事故形态”。

参考文献：

[1]崔枭翔.道路交通事故及其严重程度影响因素研究[D].大连：大连理工大学，2018.

[2]胡宗品，骆仁佳，于淑君.城市死亡交通事故形态影响因素分析[J].交通科技与经济，2022，24（1）：25-29+37.

[3]江玉杰，万征，陈继红.中国沿海水上交通事故致因路径分析[J].大连海事大学学报，2024，50（1）：76-84.

[4]李杰，陈伟炯.海因里希安全理论的学术影响分析[J].中国安全科学学报，2017，27（9）：1-7.

[5]刘畅，夏鸿文，孟兴凯，等.800 km客运班线事故特征及情景研究[J].公路交通科技，2024，41（1）：160-168.

[6]Wang W，Jiang X ，Xia S，et al.Incident tree model and incident tree analysis method for quantified risk assessment：An in-depth accident study in traffic operation[J].Safety Science，2010，48（10）：1248-1262.

[7]刘亦达.基于贝叶斯网络的高速公路蓝牌货车交通事故风险及对策研究[D].长安：长安大学，2023.

[8]熊晓夏，陈龙，梁军，等.基于贝叶斯网络模型的道路交通事故链生成与演化研究[J].公路交通科技，2018，35（5）：99-101.

[9]曹毅，周华，肖凌云，等.基于NAIS数据库中视频信息的人—车碰撞事故特征分析[J].汽车安全与节能学报，2020，11（1）：44-52.

作者简介：

容嘉，男，1998年生，硕士研究生在读，研究方向为交通安全。

何超（通讯作者），男，1980年生，教授，研究方向为汽车排放测试与控制、交通安全。