基于数据驱动的浅海波导声辐射预测方法

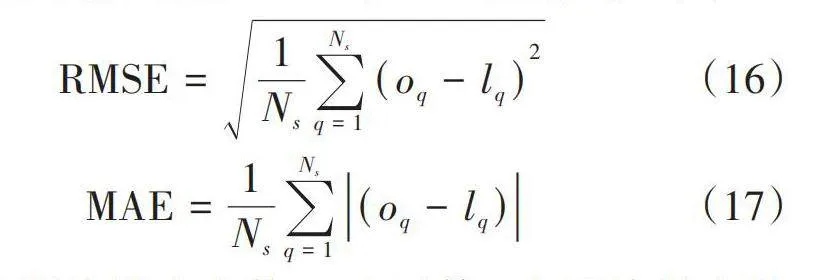
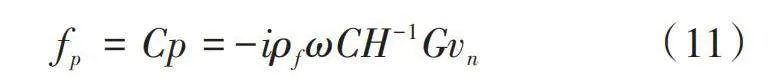
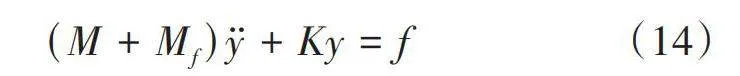
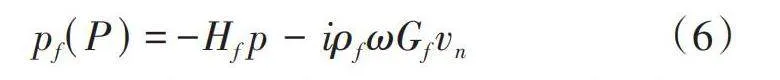
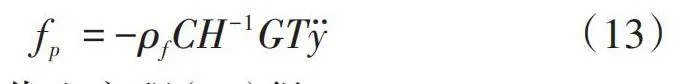
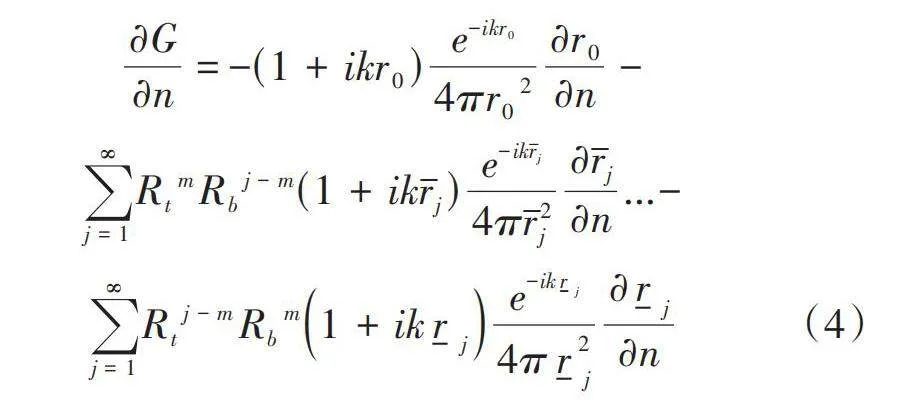
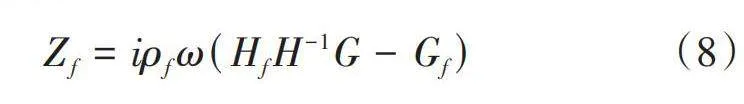
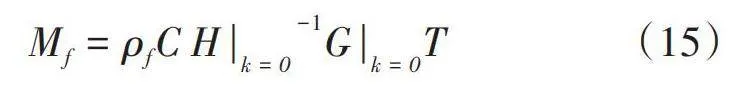
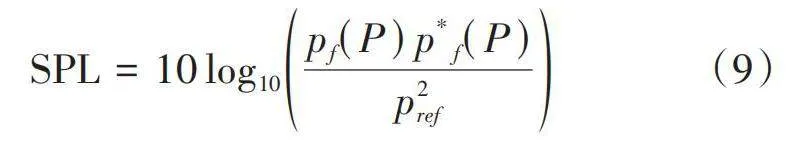
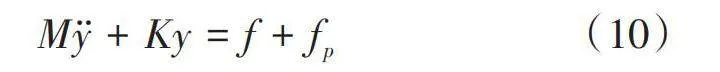
摘 要：结合计算力学和深度学习理论，提出一种基于数据驱动的浅海波导声辐射预测方法。通过集成有限元法—虚质量法—基于虚源法的边界元法的计算框架，获取浅海波导声辐射响应，为深度学习提供大量声压数据；进而，通过训练ConvNeXt卷积神经网络提取采样点声场特征；最终实现浅海水下结构辐射声压级的快速预测，并通过算例表明预测方法的有效性。

关键词：波导声辐射；基于虚源法的边界元法；ConvNeXt网络；深度学习

中图分类号：U674.70" " " "文献标识码： A 文章编号：1007 - 9734 （2024） 06 - 0095 - 08

0 序 言

海洋是人类赖以生存和发展的重要资源宝库。随着人类对海洋资源开发利用的不断深入，海洋工程结构在浅海波导环境下所产生的振动和声辐射问题日益突出，不仅影响到结构本身的安全性能和使用寿命，也对海洋生态环境造成威胁。因此，研究并控制水下声辐射具有重要的意义。

对于浸没于浅海中的结构体，其声辐射不仅由流固耦合振动决定，在声波传播过程中还受到海面和海底的强烈影响。在过去的几十年里，科研人员对结构在浅波导环境中的振动和声辐射特性进行了大量的研究，探索了多种方法来解决理想声介质中结构的声辐射问题。对于陆地边缘的海水，其环境更为复杂，在研究中经常进行许多简化。例如，假设圆柱壳结构处于无限流体中，海面和海床是自由海面、刚性海底等理想的边界条件以及声速恒定等。简化的声环境与真实海洋声环境还有一定的差距，尤其是受海面海底影响较大的浅海环境。因此，除了使用目前主流的方法如波叠加法、有限元法和边界元法等，越来越多的研究人员同时考虑了海洋波导环境中浮体结构流固耦合和声辐射，或者更复杂的边界问题。Guo等[1]提出一种用于求解浸入有限水深的有限长圆柱壳振动响应的解析方法，降低了计算成本，并采用边界元法研究考虑自由海面影响的圆柱壳的远场声辐射问题。Huang等[2]基于波叠加法，提出海洋声环境中任意声速剖面下弹性球壳流固耦合振动和声辐射的综合计算方法，并在近场和远场采用不同的水声传播模型，将近远场作为统一的系统进行分析。Chen等[3]采用双重反射法求解圆柱壳结构声辐射问题，验证其与耦合有限元/边界元法计算结果的一致性。Wang等[4]采用波传播法对水平浸入浅水中的圆柱壳在低频范围内的自由弯曲振动进行分析，同时考虑上下流体边界和附加质量的影响。Jiang等[5]提出一种考虑声速剖面的浅水结构声辐射与传播的综合计算方法，同时考虑到相对复杂的海面和海底边界条件，该方法的效率优于有限元方法，可应用于大型复杂浮体的声辐射计算。Huang等[6]采用有限元法-波叠加法计算有限水深下结构的声辐射，考虑了流固耦合效应，适用于复杂或大型轴对称结构。Zhang等[7]考虑到波导边界对声场的影响，提出一种结合射线理论和波叠加理论的方法来预测浅水中的高频辐射声场，该方法对于复杂的波导环境具有良好的适用性和计算精度。

除了计算与试验的方法，近些年兴起的数据驱动技术给出新的解决方案。深度学习可以从特定问题的数据中学习，自动分析和解决相关任务的问题。它已被证明是一种强大的数据驱动技术，目前用于处理水下声源定位问题，已经取得良好的效果[8-10]。以往的研究大多采用昂贵且耗时的试验数据来训练深度学习模型，而使用计算力学的分析方法获得大量数据来训练深度学习模型并用于水下声辐射预测的研究较少，尤其在浅海波导环境中。本文提出一种有效的数据驱动方法，用于均匀浅海环境下的声压级预测。本文主要模拟简谐激励壳结构水下声辐射，计算浅海波导环境的辐射声压级，并获得大量数据用以训练ConvNeXt深度学习神经网络[11]，训练的模型用于预测浅海环境中的辐射声压级，并通过计算误差来验证模型的性能。

1 浅海波导声辐射分析方法

1.1" 浅海波导中辐射声场的虚源边界元法

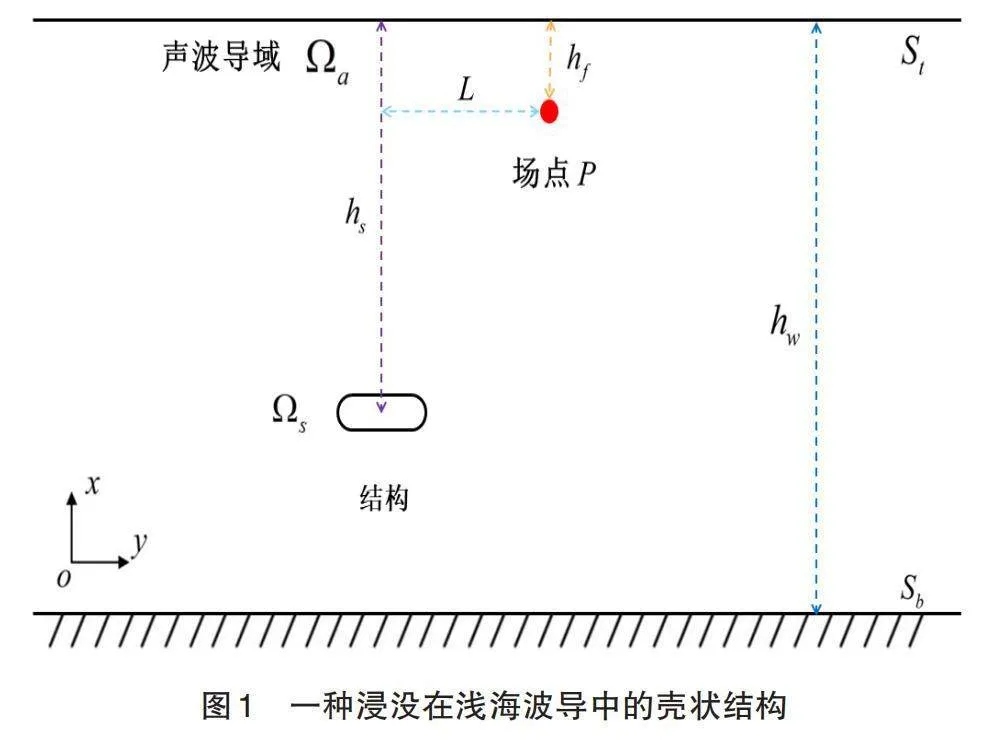
如图1所示，一个胶囊状壳结构[Ωs]浸没在声波导域[Ωa]中。其中，海面边界为St，海底边界为Sb，两者距离为水深[hw]。[hs]表示结构的潜水深度，[hf]为场点深度，L为结构中心到场点的水平距离。这个问题的亥姆霍兹积分方程是：

[CPpP=s∂p∂nQGP，Q-pQ∂G∂nP，QdS] （1）

其中，

[C（P）=1P∈Ω+a0P∈Ω-a12P∈∂Ωa] （2）

p是声压，P是目标场点，Q是结构表面[∂Ωa]的声源点，[∂p∂n=-iρfωvn]，[i=-1]，[ρf]是流体密度。[ω]是圆频率，n是结构表面指向声波导的单位法向量，[vn]是结构表面法向振动速度，G是波导格林函数，[∂G∂n]是它的法向导数，C（P）是一个常数，取决于场点P的位置，[Ω+a]和[Ω-a]分别表示结构的外侧和内侧。

理论上最简单的计算波导格林函数G的方法是虚源法。如图2所示，接收点处的声波可以看作是虚源和原始源的声波叠加，令[Rt]和[Rb]分别表示海面和海底边界的反射系数，波导Green函数的虚源解见文献[12]。

[GP，Q=e-ikr04πr0+j=1∞RtmRbj-me-ikrj4πrj+Rtj-mRbme-ikr j4πr j] （3）

其中，波数[k=ωcf] ，[cf]是流体中的声速，[r0=Q-P]表示源点Q到场点P的距离，同理，[r1=Q-P]，[r2=Q-P]…，[r 1=Q-P]，[r 2=Q-P]…，[P]和[P]分别是海面以上和海床以下的虚源，[P]和[P]的上标是反射的次数。

值得注意的是，方程（3）的第一项是自由空间格林函数，其后的级数表示虚源的贡献。由于波导的上表面为软边界，下表面为刚性边界，因此反射系数[Rt=-1]和[Rb=1]。

方程（3）对Q的坐标在n方向上求导得

[∂G∂n=-1+ikr0e-ikr04πr02∂r0∂n-]

[j=1∞RtmRbj-m1+ikrje-ikrj4πr2j∂rj∂n...-]

[j=1∞Rtj-mRbm1+ikr je-ikr j4πr2 j∂r j∂n] （4）

由于虚源解包含无限数量的虚源，因此必须对序列进行截断。设[Gn]表示在第n对虚源处截断的格林函数G的近似解。

将方程（1）离散化可得

[Hp=-iρfωGvn] （5）

其中，H和G为边界元系数矩阵，p和[vn]为声压和法向振动速度矢量。为简单起见，在对声域边界建模时，将边界元网格与有限元网格一致。在构造H和G时，忽略了波导边界对结构表面声压和法向振动的影响。

通过结构表面的声压，可获取场点P处的声压：

[pfP=-Hfp-iρfωGfvn] （6）

其中，[Hf]和[Gf]是虚源边界元系数矩阵，它取决于结构几何形状、频率和P的位置。然后，将方程（5）代入方程（6），得到

[pfP=Zfvn] （7）

声阻抗矩阵

[Zf=iρfωHfH-1G-Gf] （8）

则声压级计算公式为

[SPL=10log10pfPp*fPp2ref] （9）

其中[pref=1×10-6Pa]为水中参考声压。

1.2" 流固耦合振动的有限元—虚质量法

水下结构动力学有限元方程可表示为

[My+Ky=f+fp] （10）

式（10）中，M和K分别为结构质量矩阵和刚度矩阵。y和[y]分别是位移矢量和加速度矢量。[fp]是水动力的矢量，f是机械力的矢量。则根据方程（5），可将[fp]表示为

[fp=Cp=-iρfωCH-1Gvn] （11）

式（11）中，C为流固耦合矩阵，它将流体压力转化为等效节点力。

值得注意的是，[vn]和[y]有如下关系：

[iωvn=Ty] （12）

其中，T为变换矩阵，得到振动响应的法向分量。通过方程（12），方程（11）可进一步表示为

[fp=-ρfCH-1GTy] （13）

将方程（13）代入方程（10）得

[M+Mfy+Ky=f] （14）

式（14）中[Mf]为体现流体压力对结构动力响应影响的虚质量矩阵。假设结构周围的流体在低频时不可压缩，即波数[k=0]，则可以表示为

[Mf=ρfCHk=0-1Gk=0T] （15）

2 数据驱动方法

2.1" ConvNeXt卷积神经网络

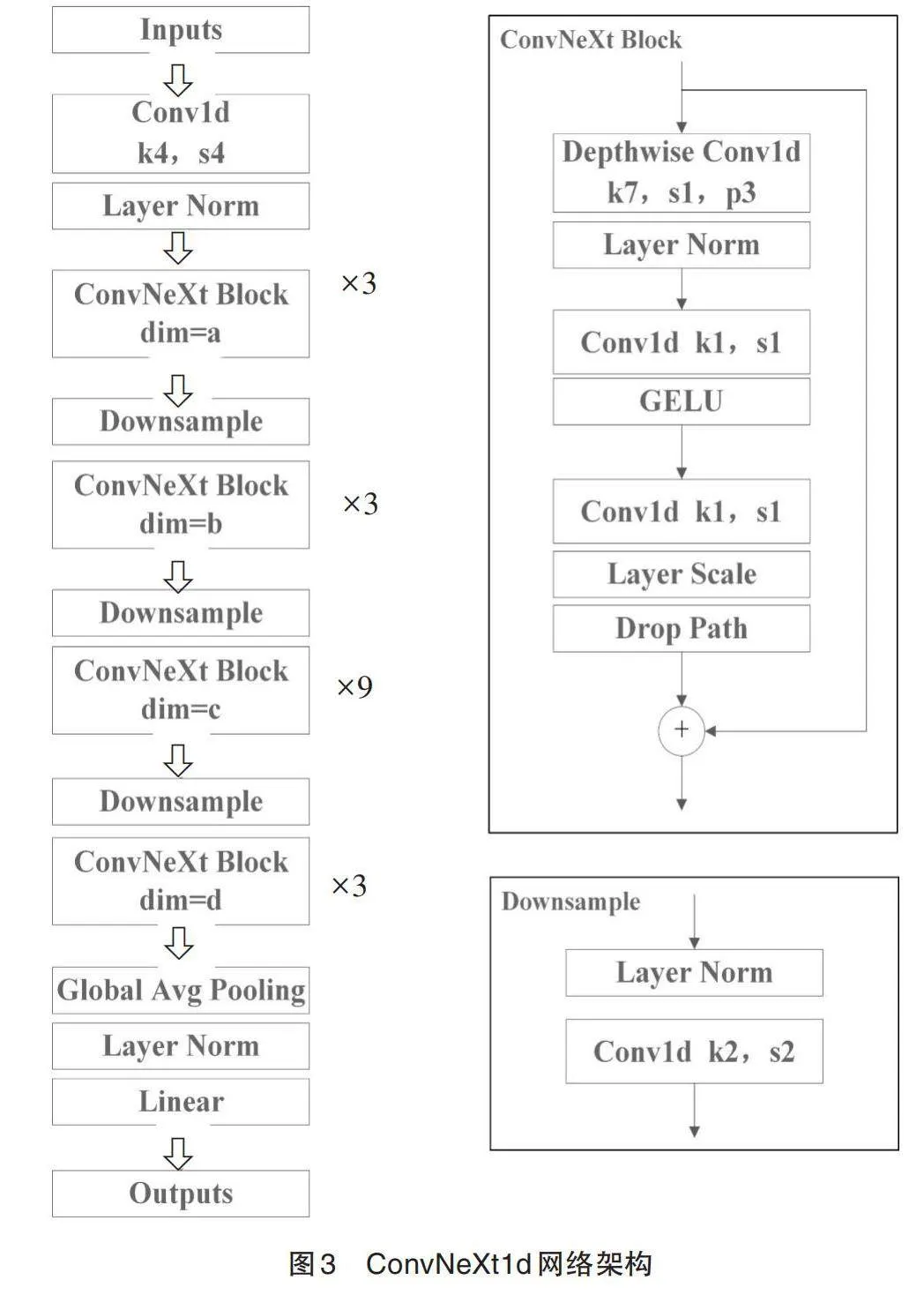
ConvNeXt网络是一种值得关注的纯卷积神经网络（CNN），它将Transformer[13]网络的一些最新思想和技术引入CNN网络的现有模块中，提高CNN网络的性能。ConvNeXt网络架构具有准确性高、可扩展性强以及架构简单等特点，但目前其在水下声辐射预测中的应用较少。本研究将计算力学的方法与深度学习相结合，使用有限元-虚拟质量法/虚源边界元法计算获得大量的声辐射数据来训练ConvNeXt网络，完成声压级的快速预测，探究其应用于水下辐射声场预测的效果。根据源代码绘制的ConvNeXt网络架构如图3所示。

本研究基于文献[11]，修改了架构的通道数，并将原文献中的二维卷积Conv2d修改为Conv1d，以使新搭建的ConvNeXt1d架构达成本研究的目标。根据上文理论方法，编程计算指定工况下的声压级数据。将场点位置、水下结构位置和材料属性等参数处理成一维数据，作为神经网络模型的输入；计算获得的一维声压级（SPL）数据，作为对应输入的预测值，为其打上标签；将训练集/验证集/测试集随机分为90%/5%/5%三个子集。训练过程中在一个小的未见过的数据集上验证评估当前模型，并检查是否有任何潜在的过拟合。本文使用平均绝对误差（MAE）作为loss函数，使用Adam优化器训练模型。采用三阶段步进学习率，每阶段的学习率分别为2[×]10-3，1.5[×]10-3和5[×]10-5，每个阶段分别训练5000，1000和1000个epoch。训练过程的前两个阶段是为了快速优化网络，之后使用5[×]10-5的学习率进行精确收敛。

2.2" 模型评估标准

为了评估下文神经网络模型的预测效果，本研究使用均方根误差（RMSE）和平均绝对误差（MAE）作为模型的评价函数。MSE与MAE的公式如下：

[RMSE=1Nsq=1Ns oq-lq2] （16）

[MAE=1Nsq=1Ns oq-lq] （17）

其中，Ns为训练样本个数，oq表示第q个训练样本的输出值，lq表示第q个训练样本的值。

2.3" 工作流程

本文的具体工作流程如图4所示。

首先，利用浅海波导声辐射模型计算获得声压级数据，然后把数据处理成适合深度学习模型的一维形式，并划分为训练集，验证集和测试集。其次，将训练数据集输入到构建的深度学习模型中进行训练。最后，对训练的模型性能进行了测试，将预测结果与计算数据进行比较，验证该方法的准确性。

3 实验研究

3.1" 浅海波导声辐射数值的获取

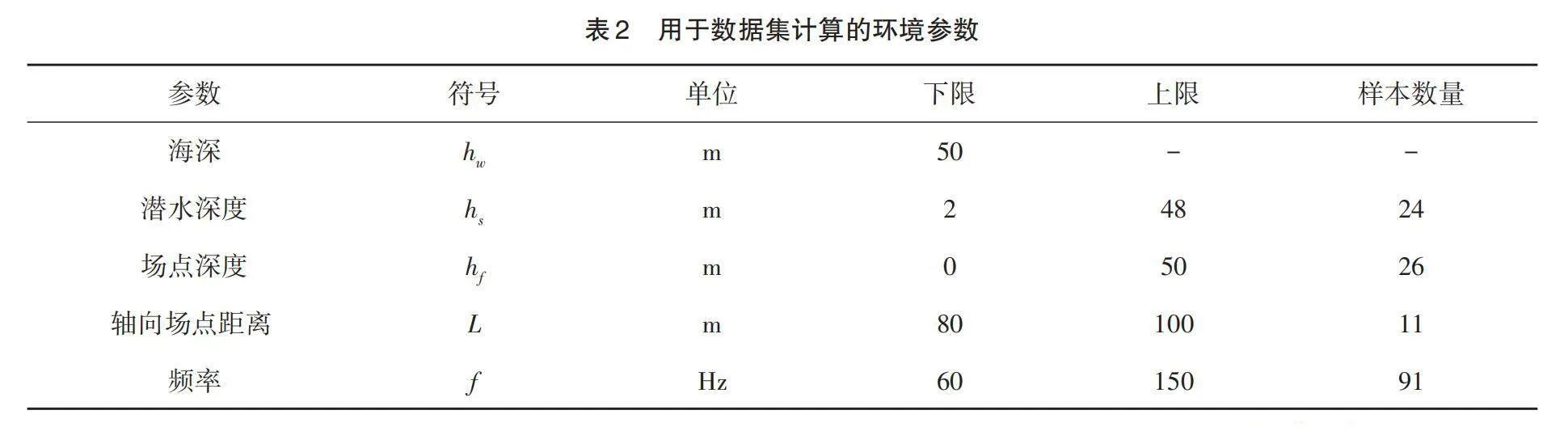
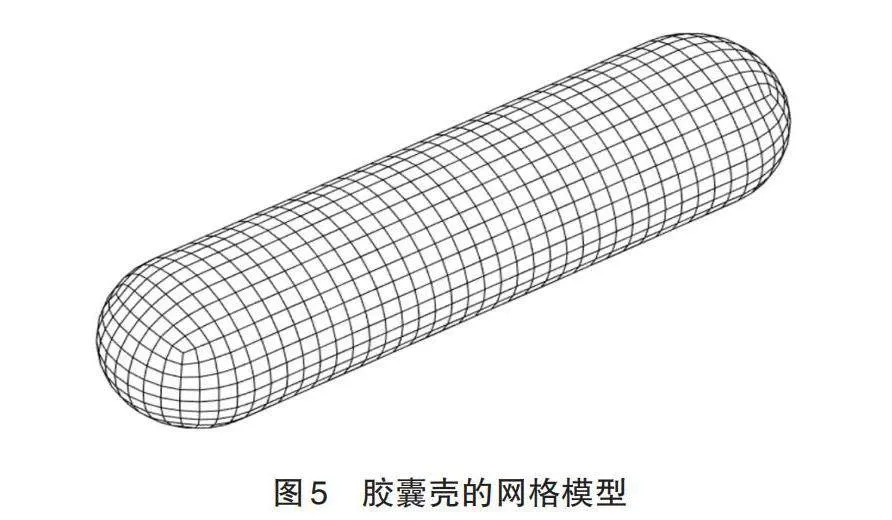
考虑一个结构[Ωs]浸没在浅海波导[Ωa]中，如图1所示。假设海面边界为完全软边界，海底为完全刚性边界。胶囊状壳结构如图5所示，其半径为0.5 m，侧面圆柱长度3 m，厚度为0.008 m。该结构由1344个离散的薄壳单元构成，声学边界划分了1344个四边形单元网格。表1列出了详细的材料和海水参数。结构潜水深度、场点深度和场点轴向方向的采样距离均间隔2 m。在结构表面垂向施加振幅为100 N，频率范围在60 Hz-150 Hz的简谐力，加载位置为侧面中心点。每增加1 Hz，计算该条件下不同场点的声压级数据，得到数据集的详细环境参数见表2。

3.2" 训练模型与实验结果

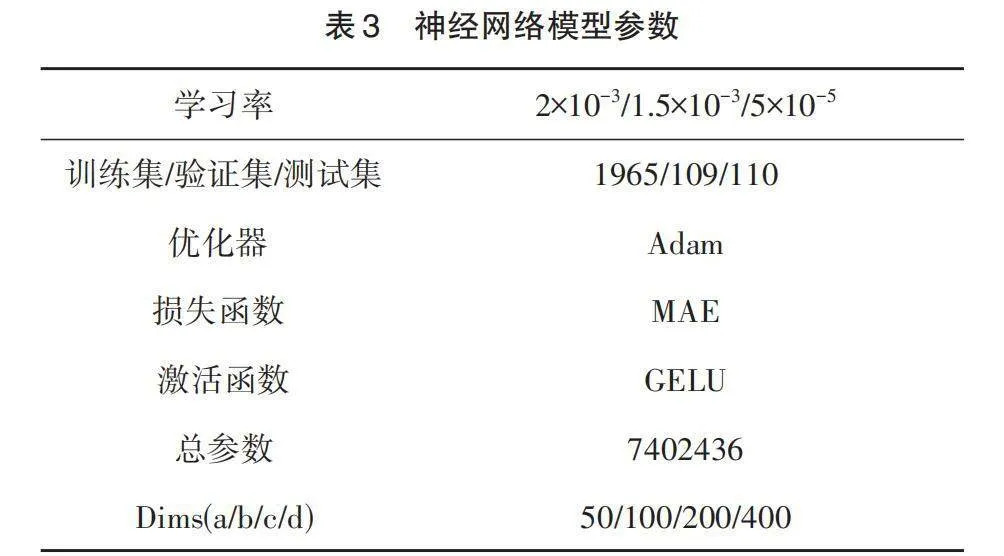
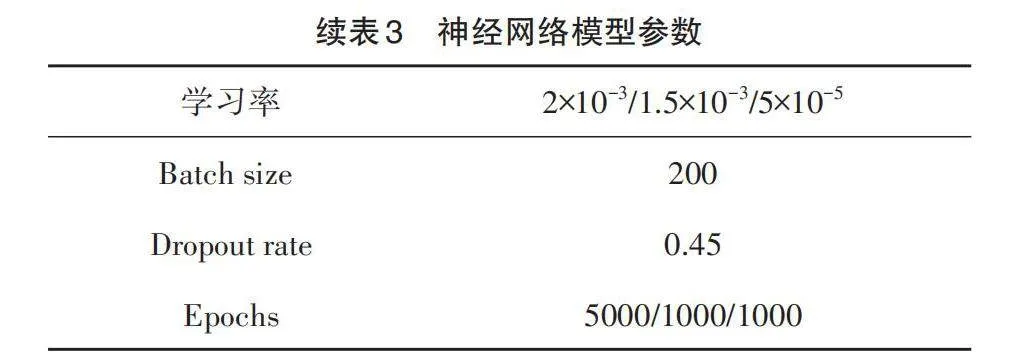
这里使用1965个样本来训练ConvNeXt网络。表3给出了模型结构参数，以及用于训练模型的其他超参数的值。

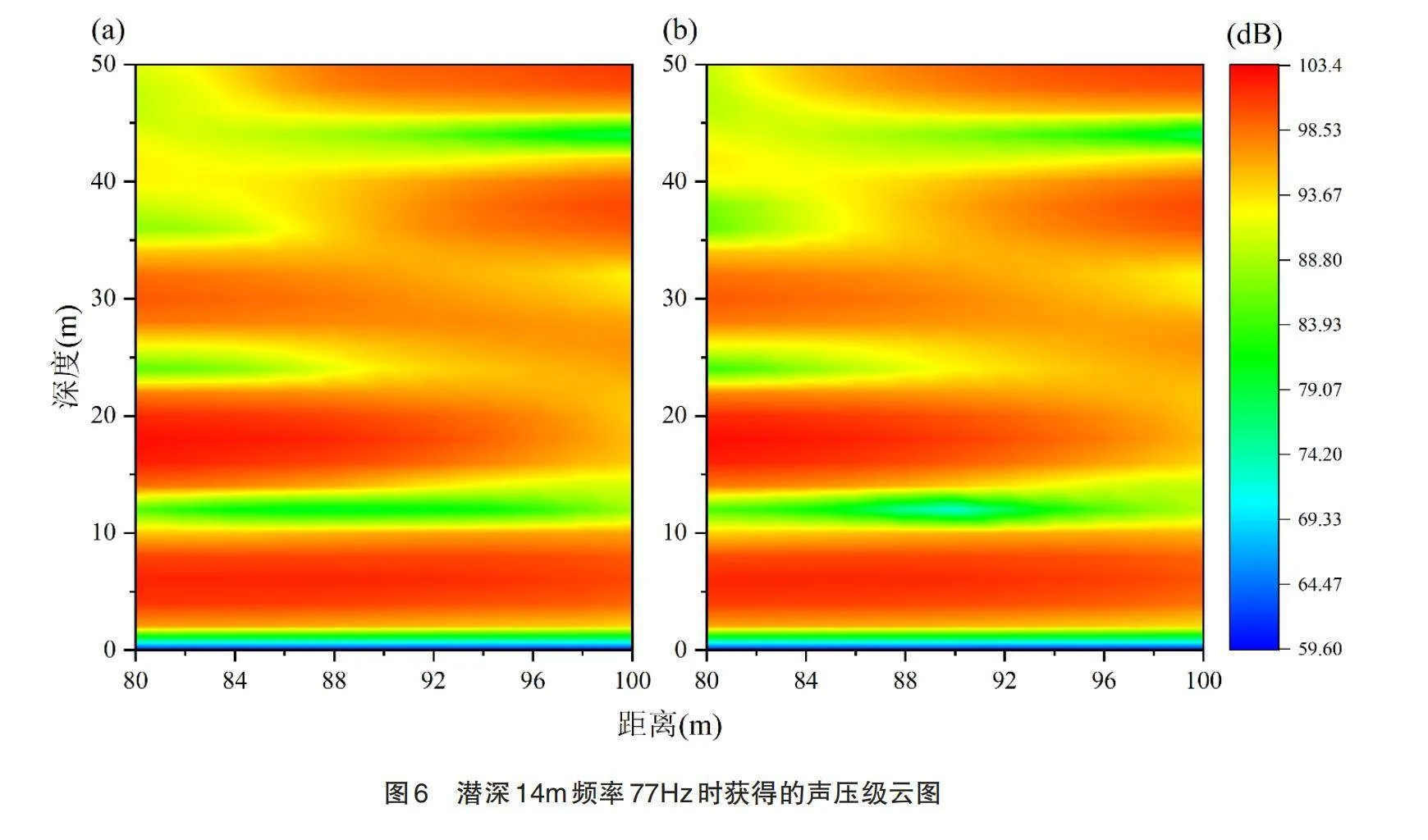
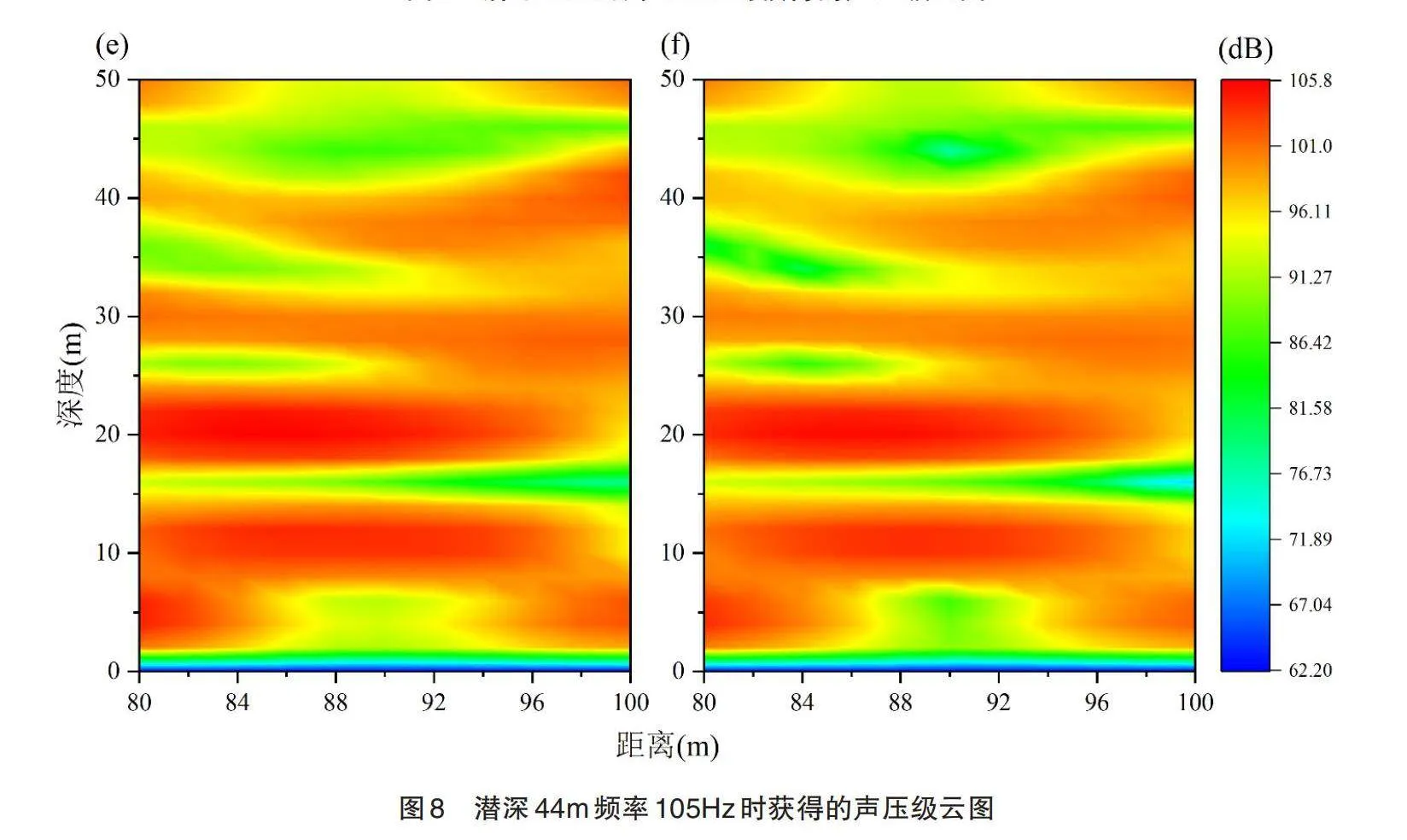
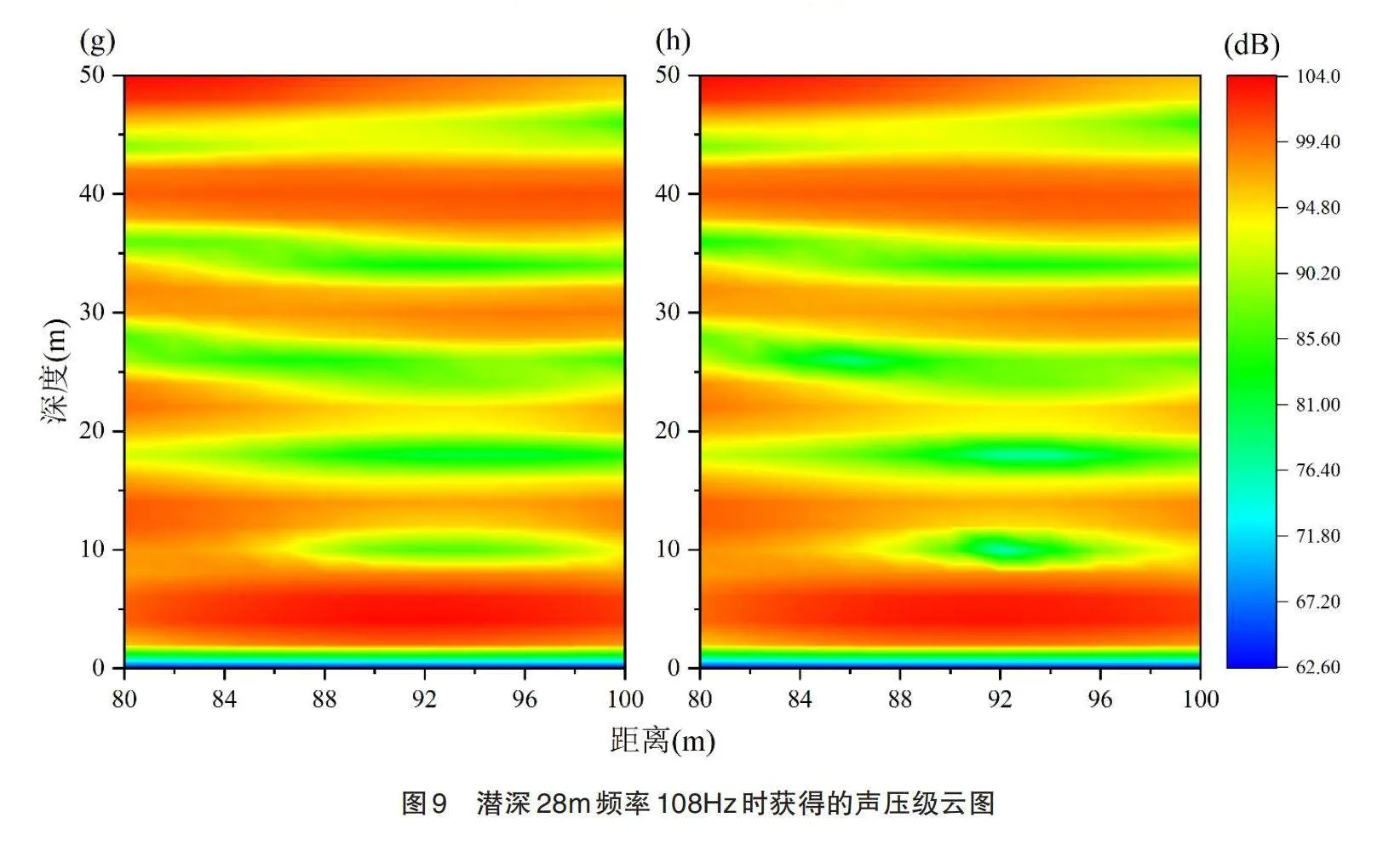
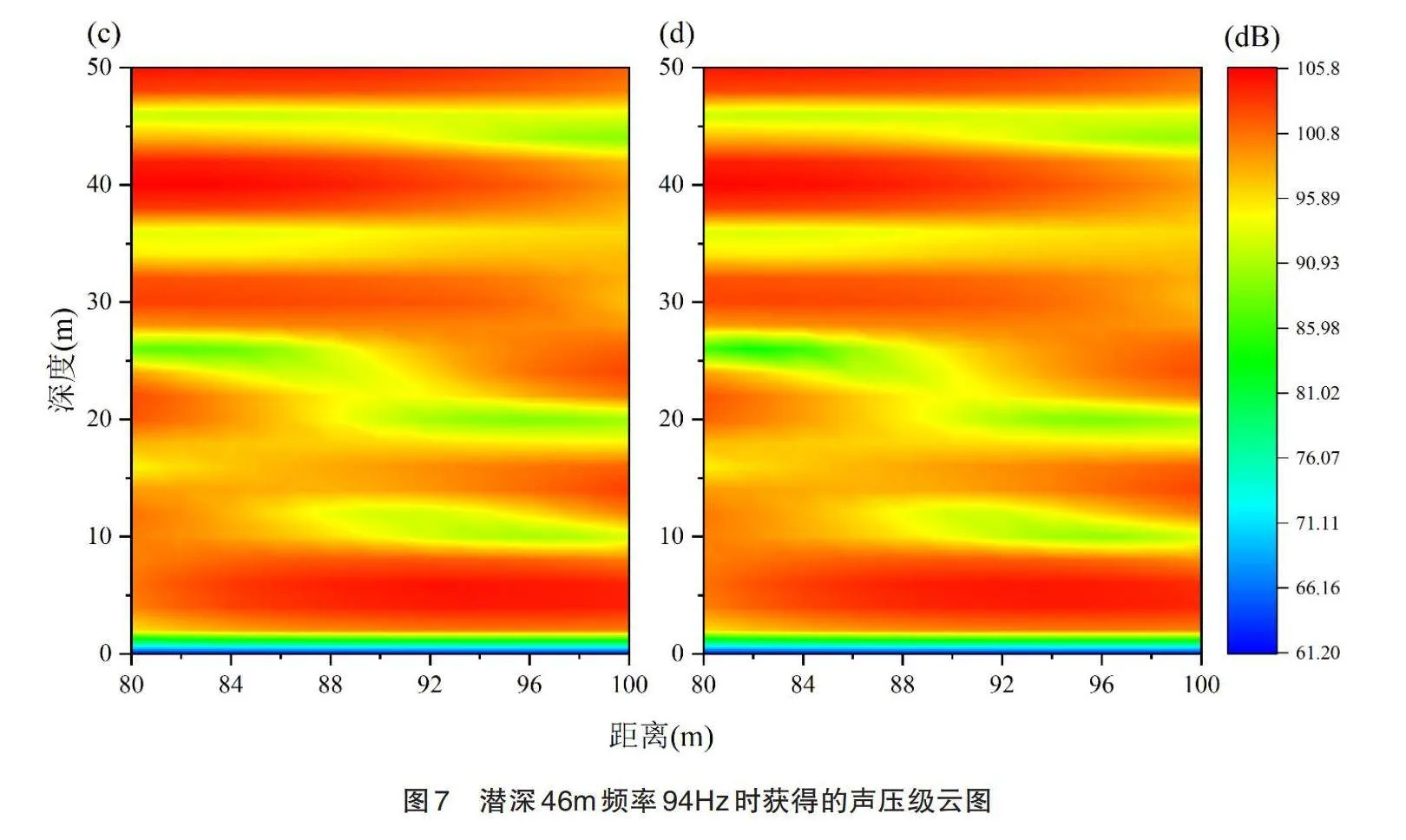
图6到图9展示了深度学习神经网络预测的数据与程序计算获得数据的对比情况，他们以某一频率下的声压级云图的形式呈现。其中图6的物理信息是潜深14 m，频率为77 Hz；图7为潜深46 m，频率为94 Hz；图8为潜深44 m，频率为105 Hz；图9为潜深28 m，频率为108 Hz。（a）、（c）、（e）和（g）是根据神经网络预测获得数据绘制的，（b）、（d）、（f）和（h）是由数值仿真获得数据绘制。图中横轴表示场点到结构的距离，取值范围为80 m～100 m，纵轴表示海水深度，取值范围为0～50 m。对比每组云图，每两张中只有较少的不一致区域，体现了神经网络优异的预测性能。神经网络的统计指标RMSE和MAE如图10所示。可以看出，误差值均在4 dB以内，说明网络模型取得了较好的训练效果。以上结果表明，该神经网络模型取得了较好的声辐射预测效果。

3.3" 与其他网络架构的对比

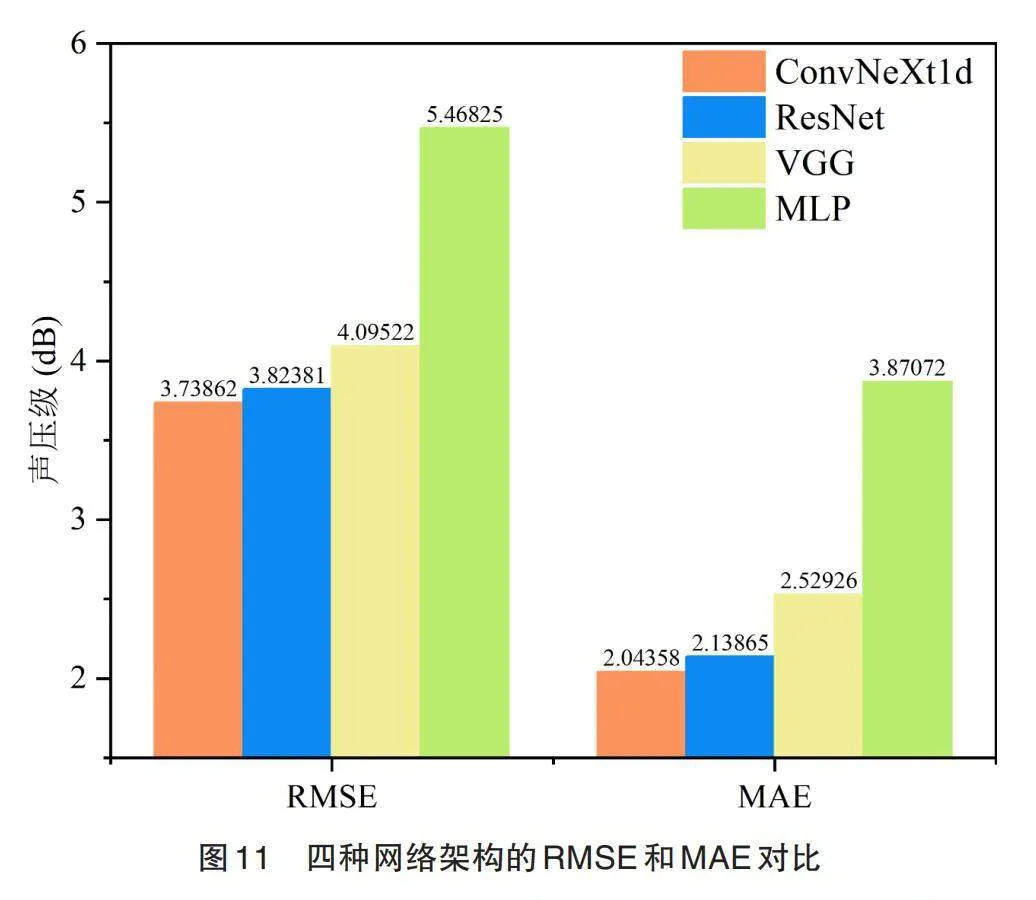
本研究提出的ConvNeXt1d架构是一个准确且高效的预测方法。为了体现该方法的优越性，本文将该网络架构与其他常见网络架构的预测结果进行对比评估。其中包括多层感知机（MLP）、Visual Geometry Group（VGG）、残差神经网络（ResNet）等架构。几种对比方法的输入层与输出层均和本文架构一致，模型参数更新采用的反向传播、使用的Adam优化算法、epochs和MAE作为损失函数也都与本文设置相同。将不同方法预测的结果整合在一起，通过RMSE和MAE作为标准进行评价，结果如图11所示。

不难看出，ConvNeXt1d、ResNet和VGG几种方法在测试集上均表现不错，其中本文提出的ConvNeXt1d方法表现最好，MLP表现较差。总而言之，本文方法取得了较好的声辐射预测效果，对比其他方法也具有一定的优势。

4 总 结

本文提出一种基于数据驱动的浅海波导声辐射预测新方法，通过有限元-虚质量-基于虚源法的边界元法的数值计算框架，获取浅海波导域内样本点处辐射声压级，并将结果数据作为数据集训练ConvNeXt深度学习网络，最终用于水下声辐射的预测。结果表明，该方法可以快速完成胶囊状壳体结构目标工况下的声辐射预测，并且取得较好的预测效果。本研究为浅海水下快速声辐射预测提供了一种有效的手段。然而，对于更加复杂浅海环境下的预测问题，如何快速获取大量数据，仍待未来深入研究。

参考文献：

［1］GUO W，LI T，ZHU X，et al.Vibration and acoustic radiation of a finite cylindrical shell submerged at finite depth from the free surface ［J］.Journal of Sound and Vibration，2017，393：338-352.

［2］HUANG H，ZOU M S，JIANG L W.Study on the integrated calculation method of fluid-structure interaction vibration，acoustic radiation，and propagation from an elastic spherical shell in ocean acoustic environments ［J］.Ocean Engineering，2019，177：29-39.

［3］CHEN L，LIANG X，YI H.Vibro-acoustic characteristics of cylindrical shells with complex acoustic boundary conditions ［J］.Ocean Engineering，2016，126：12-21.

［4］WANG P，LI T，ZHU X.Free flexural vibration of a cylindrical shell horizontally immersed in shallow water using the wave propagation approach ［J］.Ocean Engineering，2017，142：280-291.

［5］JIANG L，ZOU M，HUANG H，et al.Integrated calculation method of acoustic radiation and propagation for floating bodies in shallow water ［J］.J Acoust Soc Am，2018，143（5）：430-436.

［6］HUANG H，ZOU M S，JIANG L W.Study on calculation methods for acoustic radiation of axisymmetric structures in finite water depth ［J］.Journal of Fluids and Structures，2020，98：103115.

［7］ZHANG C，LIU Y，SHANG D，et al.A method for predicting radiated acoustic field in shallow sea based on wave superposition and ray ［J］.Applied Sciences，2020，10（3）：917.

［8］NIU H Q，GONG Z X，OZANICH E，et al.Deep-learning source localization using multi-frequency magnitude-only data ［J］.J Acoust Soc Am，2019，146（1）：211-222.

［9］HUANG Z Q，XU J，GONG Z X，et al.Source localization using deep neural networks in a shallow water environment ［J］.J Acoust Soc Am，2018，143（5）：2922-2932.

［10］HUANG Z，XU J，GONG Z，et al.Multiple source localization in a shallow water waveguide exploiting subarray beamforming and deep neural networks [J].Sensors，2019，19（21）：4768.

［11］LIU Z，MAO H，WU C Y，et al.A convnet for the 2020s; proceedings of the IEEE/CVF conference on computer vision and pattern recognition，F，2022[C].

［12］WU T.On computational aspects of the boundary element method for acoustic radiation and scattering in a perfect waveguide[J].The Journal of the Acoustical Society of America，1994，96（6）：3733-3743.

［13］LIU Z，LIN Y，CAO Y，et al.Swin transformer：hierarchical vision transformer using shifted windows; proceedings of the IEEE/CVF international conference on computer vision，F，2021[C].

责任编校：刘 燕，孙咏梅

A Data-Driven Method for Predicting Shallow Sea Waveguide

Acoustic Radiation

ZHAI Jingjuan ，FU Ning ，SHANG Linyuan*

（College of Aerospace Engineering，Shenyang Aerospace University，Shenyang 110136，China）

Abstract：This article combines computational mechanics and deep learning theory to propose a data-driven shallow water waveguide acoustic radiation prediction method.Integrating finite element method，virtual mass method，and boundary element method based on virtual source method，a computational framework for vibration sound radiation of structures in shallow seawater has been developed to obtain waveguide sound radiation response and provide a large amount of sound pressure data for deep learning.Furthermore，by training ConvNeXt convolutional neural network，the sound field features of sampling points are extracted.Ultimately，the rapid prediction of radiation sound pressure levels for structures in shallow seawater is achieved.The numerical results demonstrate the effectiveness of the proposed shallow water waveguide acoustic radiation prediction method.

Key words：waveguide acoustic radiation；boundary element method based on virtual source method；ConvNeXt network；deep learning