福建中考数学几何试题特点及学生解题策略研究

作者简介：林蕉苹（1982～），女，汉族，福建福州人，福建省漳州市第三中学，研究方向：数学教学。

摘 要：文章以福建省中考数学几何试题为研究对象，对近年来福建中考数学几何试题进行分析，总结了试题的特点，并针对学生解题过程中存在的问题，提出了相应的解题策略。研究发现，福建中考数学几何试题重视基础知识的考查，注重考查学生的空间想象能力、逻辑推理能力和数形结合思想，也重视与实际生活的结合。为此，学生应掌握基本定理和公式，加强图形的观察与分析，灵活运用数形结合的方法，培养良好的解题习惯。

关键词：福建中考；数学试题；几何；解题策略

中图分类号：G633.6 文献标识码：A 文章编号：1673-8918（2024）42-0086-04

数学是中考的重要科目之一，其中几何部分占有较大比重。福建省的中考数学试题题型灵活多变、注重能力考查。文章将对福建中考数学几何试题的特点进行分析，并针对学生解题过程中的问题提出相应对策，以期对初中数学教学提供参考。

一、福建中考数学几何试题的特点

（一）重视基础知识的考查

福建中考数学几何试题注重对基础知识的考查，试题涵盖了初中阶段所学的各个几何知识点，如图形的基本性质、全等三角形、相似三角形、平行线、圆、投影与视图等。这些基础知识是解题的前提和基础，只有扎实掌握这些知识，才能在解题过程中熟练运用。

（二）注重考查学生的空间想象能力

空间想象能力是学习几何的重要能力之一，福建中考数学几何试题通过多样化的题型，如立体图形的三视图、展开图、旋转与平移等，考查学生对空间图形的想象与理解。这些试题要求学生在头脑中形成清晰的空间图像，并能灵活地对图像进行移动、变换和重组。

例题1：已知一个长方体ABCD—A′B′C′D′，其中AB=3 cm，BC=4 cm，AA′=5 cm，点P是棱B′C′上的一点，若BP⊥CC′，求BP的长度。

解析：本题考查学生对长方体空间位置关系的理解和空间想象能力。学生需要在脑海中想象出长方体的形状，并根据已知条件，利用空间向量或者勾股定理求解BP的长度。

（三）考查学生的逻辑推理能力

几何证明题是考查学生逻辑推理能力的重要题型，福建中考数学试题中几何证明题的比重较大，这些试题通过已知条件和待证结论，考查学生的逻辑推理和论证能力，学生需要根据几何定理和公理，通过演绎推理得出结论，论证过程要严谨、缜密。

例题2：在Rt△ABC中，∠C=90°，CD⊥AB于D，CE平分∠ACB，证明：AD=BD。

解析：本题考查学生对直角三角形性质的理解和逻辑推理能力，学生需要根据已知条件，利用三角形的全等条件、中线定理等，通过逻辑推理论证出AD=BD。

（四）体现数形结合的思想

数形结合是数学的基本思想之一，其在福建中考数学几何试题中多有体现。试题通过将代数方法与几何知识相结合，考查学生的解题能力。学生需要灵活运用所学的数学知识，通过代数计算解决几何问题，或者通过几何图形的性质分析简化代数计算。

例题3：在矩形ABCD中，AB=3 cm，BC=4 cm，点P在对角线AC上，且∠PDC=45°，求AP的长度。

解析：本题考查学生数形结合的能力，学生可以利用矩形的性质，通过勾股定理求出对角线AC的长度，再利用三角函数求出AP的长度，体现了几何性质与代数计算的结合。

（五）联系实际生活

福建中考数学几何试题注重联系实际生活，经常通过生活化的题材考查学生的数学应用能力。这些试题将几何知识与实际问题相结合，学生需要运用所学知识解决实际问题。

例题4：某学校操场是一个半圆形，直径长100米，现需要在操场边缘铺设一圈跑道，跑道宽2.5米，铺设跑道需要多少平方米的面积？（π取3.14）

解析：本题将几何知识与实际生活相结合，考查学生的应用能力。学生需要根据半圆形操场的形状，利用圆的面积公式，求出跑道的面积，体现了几何知识在实际问题中的应用。

综上所述，福建中考数学几何试题重视基础知识，注重考查学生的空间想象能力、逻辑推理能力和数形结合的思维方式，同时，注重联系实际生活。这些特点反映了试题的全面性和综合性，对学生的几何素养提出了较高的要求。

二、学生解题存在的问题

（一）基础知识掌握不扎实

基础知识是解决几何问题的前提和基石，如果学生对基本定理、公式和性质掌握不牢、理解不透，就会在解题过程中束手无策，难以找到突破口。具体来说，学生在以下几何知识点方面经常出现问题：

1. 平行线知识

平行线是几何学习的重要内容，涉及平行线的判定、性质、证明等多个方面，学生往往对以下知识点掌握不清：平行线的判定定理：同位角相等、内错角相等、同旁内角互补等。平行线的性质定理：两直线平行于第三条直线，则这两直线平行；两直线截割一组平行线，所得的同位角、内错角、同旁内角分别相等。平行线的证明方法：利用三角形全等、角平分线、梯形的性质等。学生常常混淆这些概念，在遇到平行线问题时思路不清，解题速度慢。

2. 全等三角形与相似三角形

全等和相似是研究三角形的重要方法。学生对以下知识点的混淆会导致解题障碍：全等三角形的判定定理：SAS、ASA、AAS、HL、SSS（不常用）。相似三角形的判定定理：AA、SAS、SSS（其中AA最常用）。全等三角形的性质：全等三角形对应边相等，对应角相等。相似三角形的性质：相似三角形对应角相等，对应边成比例。学生常常记不清全等和相似的条件，或者搞不清全等和相似的异同，从而无法正确运用相关性质进行证明。

3. 圆的知识

圆是平面几何的重要内容，涉及圆的性质、圆与直线的关系、圆与圆的关系等。学生易犯的错误有：搞不清圆心角、圆周角、弧、弦等基本概念，记不住圆周角定理、弦切角定理、弦弦角定理等重要定理，混淆切线的判定、性质与证明方法，对圆的位置关系（内切、外切、相交）缺乏直观理解。

只有打牢基础，才能在解题时做到快速反应、融会贯通。教师在教学中，也应重视基础知识的教学，通过测试讲评、知识梳理等教学环节，帮助学生夯实知识根基，掌握解题的基本功。

（二）空间想象能力欠缺

空间想象能力是解决立体几何问题的关键，然而，许多学生的空间想象能力较为欠缺，难以在脑海中形成清晰的立体图像，尤其对图形的位置关系和空间变换缺乏直观认识，导致学生在解题时无法准确分析图形，难以找到解题的突破口。

（三）逻辑推理能力缺乏

逻辑推理能力是几何证明题的核心要求，一些学生在证明题中表现出逻辑推理能力的不足，主要表现为：证明思路不清晰、论证不严谨、无法找到合适的证明方法等，这导致学生在解题时思路混乱，难以得出正确结论。

（四）数形结合思想运用不够

数形结合是解决几何问题的重要思想方法，但一些学生在解题时对数形结合的运用不够熟练。主要表现为：不善于用代数方法解决几何问题，不能很好地将图形转化为数量关系，对代数与几何知识的综合运用不够灵活等，导致在解题时思路受限，难以发挥数形结合的优势。

例题：在△ABC中，AB=AC，D是BC上的点，且AD平分∠BAC，证明：BD=CD。

解析：这道题考查学生的逻辑推理能力，学生需要根据已知条件，通过演绎推理得出结论。如果学生无法找到合适的证明思路，如利用全等三角形或者角平分线的性质，就难以完成证明过程。

（五）审题能力有待提高

审题能力是解题的基础，但一些学生在解题时存在审题不仔细、理解不准确的问题。主要表现为：遗漏重要条件、误解题意、未能把握问题的关键等，这导致学生在解题时走入误区，得出错误结论。

针对以上问题，教师应加强学生基础知识的学习，培养学生的空间想象能力和逻辑推理能力，指导学生灵活运用数形结合的思想方法，并提高学生的审题能力。同时，教师应指导学生加强习题训练，通过多样化的题型帮助学生巩固知识，提高解题能力。

三、学生解题策略

（一）夯实基础知识，掌握基本定理和公式

几何学习的基础是扎实的定理和公式功底，学生应熟记并理解各种几何图形的性质、判定定理、计算公式等基本知识。只有对这些知识点烂熟于心，才能在解题时迅速调用、灵活运用。建议学生重视基础知识的学习和巩固，在记忆的基础上，深入理解其中的原理和推导过程，形成完整的知识体系。同时，还要注重练习和应用，通过大量习题巩固知识，提高运算能力。教师要引导学生系统复习重点知识，查缺补漏，并适时进行测试和强化训练。

（二）加强图形观察与分析，提高空间想象能力

空间想象能力是学习几何的重要基础，学生要学会从不同角度观察分析图形，在头脑中形成清晰的空间图像，并能对图像进行移动、变换、组合等。建议学生多观察生活中的几何形体，并进行主动分析和思考，可以借助实物模型、多媒体演示等直观教具，加深对图形的理解。同时，还要多做空间想象题，如对图形进行ba767f0104acb8fa9c46dcf5362f4633aba043c31200a56e5e011753761469c8截切、折叠、旋转等操作，锻炼思维的灵活性。教师则要创设形象生动的教学情境，引导学生探索图形的多面性，培养学生由直观到抽象、由具体到一般的思维能力。

（三）重视逻辑推理，培养严密的数学思维

几何证明离不开严密的逻辑推理，学生要养成抽丝剥茧、环环相扣的思维习惯，做到论证过程严谨缜密，层次分明。要学会运用演绎、归纳等推理方法，根据已知条件逐步推出结论，做到有理有据。建议学生重视逻辑思维的训练，多做需要推理论证的题目。解题时要学会把握题目条件，理清推理线索，列出论证思路，每一步都做到有根有据。平时也可以阅读一些数学史料、名家证明，学习严谨的数学语言和规范的表述方式。教师则要注重引导学生树立形式化思维，鼓励学生尝试多种证明方法，培养不怕困难、敢于质疑的探究精神。

（四）运用数形结合，提高解题能力

数形结合是数学的重要思想方法，在解决几何问题时，学生要学会利用代数方法将图形抽象为数量关系，再用数学运算揭示事物的内在联系，从而探求问题的解决途径。建议学生加强代数和几何知识的融合，理解二者的内在联系。解题时要善于从图形中提取数量信息，灵活运用坐标系、参数方程、向量、三角函数等工具，将问题转化为代数运算。同时，还要注重从几何直观中领悟代数法则，用形象思维理解数学抽象。教师则要引导学生发现数形结合的典型例题，启发学生从多角度分析问题的数学实质，体会数学的简洁与美妙。

综上所述，要提高几何解题能力，学生应从夯实基础、观察分析、逻辑推理、数形结合、规范习惯等方面入手，教师则要从多角度引导学生，激发学生学习兴趣，培养学生的数学思维和创新意识，促进学生几何核心素养的全面发展。

四、例题分析

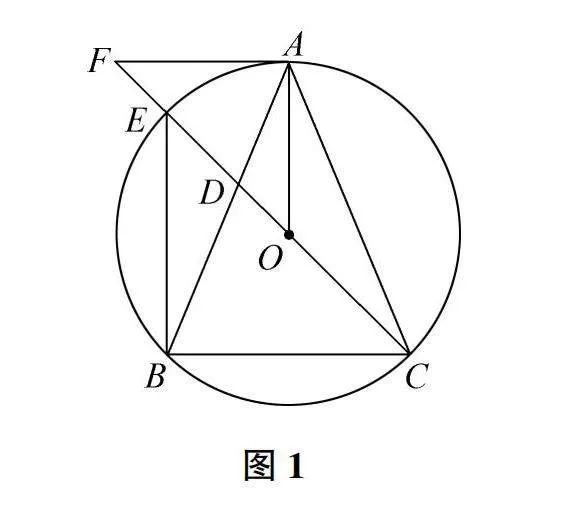
如图1，已知△ABC内接于⊙O，CO的延长线交AB于点D，交⊙O于点E，交⊙O的切线AF于点F，且AF∥BC。（1）求证：AO∥BE；（2）求证：AO平分∠BAC。

（1）求证：AO∥BE

证明：①连接OB，在△ABC中，OC⊥AB（△ABC的内心性质），∴∠OCB=90°。②∵CO延长线交AB于点D，∴∠OCD=90°（∵∠OCB=90°）。③∵在⊙O中，OC为直径，∴∠OEB=90°（圆周角定理）。④∵∠OCD=∠OEB=90°，∴BE⊥OC。⑤∵AO⊥OC（△ABC的内心性质），∴AO∥BE。

解析：本题考查学生运用圆周角定理、三角形内心的性质进行逻辑推理证明的能力。证明过程需要学生深刻理解并灵活运用以下知识点：（1）内接三角形内心的性质：内心到三边的距离相等，内心与外心、重心的连线互相垂直；（2）圆周角定理：圆周角所对的弧度数为圆心角的一半，直径所对的圆周角为直角；（3）平行线判定定理：两直线垂直于同一直线，则这两直线平行。要完成证明，学生需要进行缜密的逻辑推理，层层递进，体现了严谨的数学思维。

（2）求证：AO平分∠BAC

证明：①连接BO，在△ABC中，AO=BO（△ABC的内心性质），∴△ABO是等腰三角形。②∵△ABO是等腰三角形，∴∠BAO=∠ABO。③∵AF∥BC，∴∠BAF=∠ACB（同位角）。④∵∠ABO=∠BAF（∵圆周角∠BEF所对弧∠BAF=圆心角∠BOA的一半），∴∠BAO=∠BAF=∠ACB。⑤∴AO平分∠BAC。

解析：本题进一步考查了学生综合运用三角形内心性质、圆周角定理、平行线性质进行逻辑推理的能力。在证明过程中，学生需要发现△ABO是等腰三角形，从而得出∠BAO=∠ABO，然后利用平行线的同位角性质，得出∠BAF=∠ACB，再利用圆周角定理，得出∠ABO=∠BAF。通过层层推理，最终得出AO平分∠BAC的结论。这个过程体现了由特殊到一般、由局部到整体的数学思想，需要学生具有全局观念和缜密思维。

通过以上分析，我们可以将这道题的解题策略总结如下：①明确已知条件和结论目标，把握题目中的几何元素（如△ABC、⊙O等），构建解题思路。②运用三角形内心的性质（如内心到三边等距离、垂直于外心和重心的连线等），结合题目条件进行推理。③灵活运用圆的性质（如圆周角定理、直径所对圆周角为直角等），探究图形之间的内在联系。④善于利用平行线的性质（如同位角相等），将不同位置的角度联系起来，简化推理难度。⑤层层推进，步步为营，进行严密的逻辑论证，最终得出结论，让每一步推理都经得起推敲。⑥注重解题过程的规范性，在草稿纸上将图形画清楚，将推理步骤一一列出，让他人能看懂解题思路。

参考文献：

［1］王秋娟.探究解题策略内化数学思想——例谈中考数学压轴题的解题策略［J］.数理化解题研究，2024（2）：71-73.

［2］唐雪儿.核心素养视角下的数学中考试卷分析［D］.上海：华东师范大学，2022.

［3］雷秀花.基于推理能力的福建省中考数学试题研究［D］.闽南师范大学，2022.

［4］曹瑾.中考数学二次函数压轴题常见题型及解题策略［J］.数理天地（初中版），2024（5）：50-52.

［5］陈平.运算素养视角下高中数学解题教学策略研究——以某一圆锥曲线综合问题为例［J］.数理化解题研究，2024（6）：56-58.

［6］巩莹.基于思维可视化的小学数学解题策略研究［J］.教育艺术，2024（2）：33-34.