利用轴对称求线段和最值

求线段和的最值问题是中考的热点，利用轴对称性质对已知线段进行转移拼接，是解决这类题的基本方法. 下面举例介绍，供同学们参考.

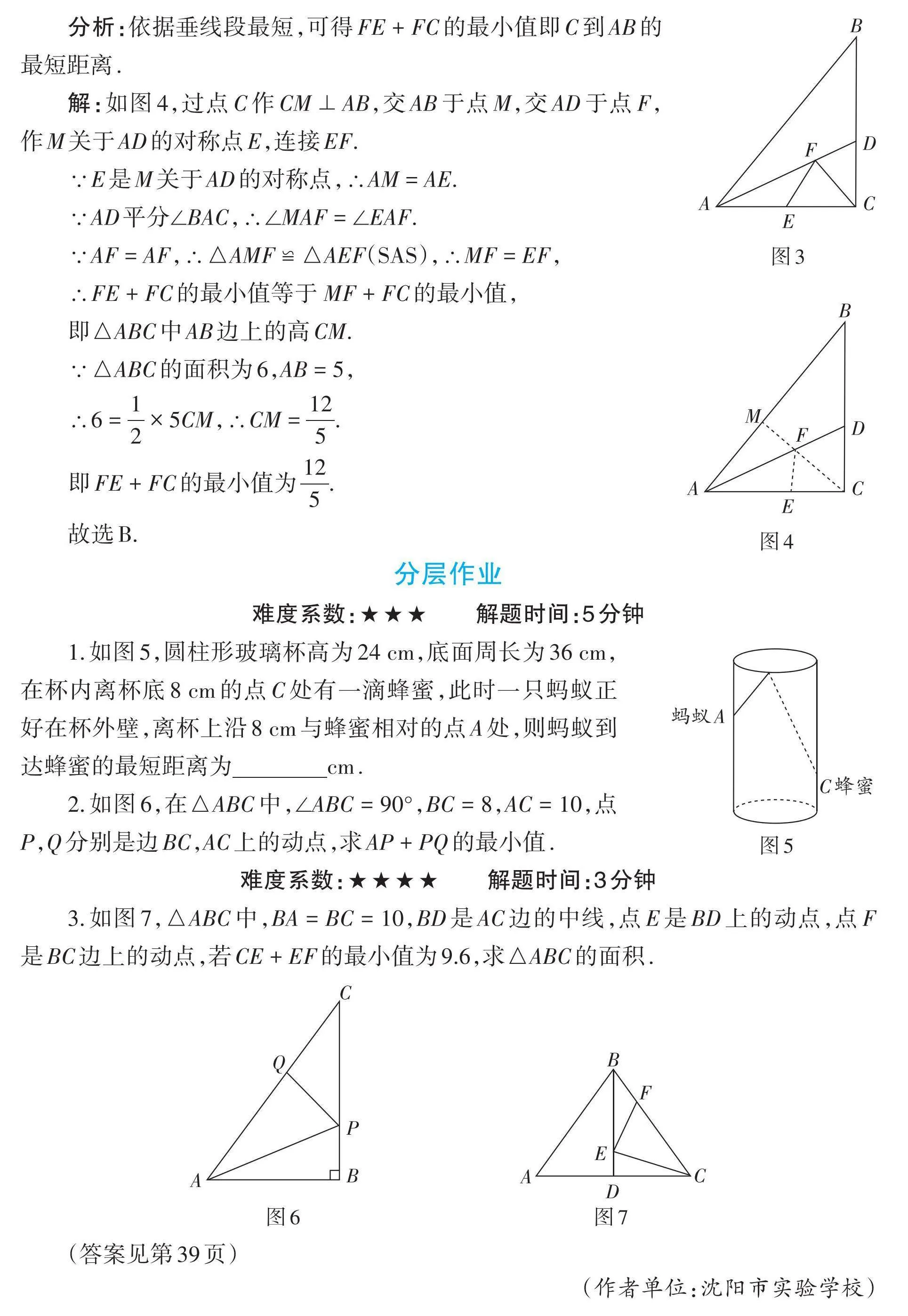
例1 如图1，在等腰三角形ABC中，AB = AC = 5，AD是△ABC的高，BC = 6，E，F分别是AB，AD上一动点，则BF + EF的最小值为 .

分析：连接CF，CE，如图2，由等腰三角形的性质得到AD垂直平分BC，BD = CD = 3，点B关于AD的对称点是点C，则BF = CF，故当C，E，F三点共线且CE ⊥ AB时，BF + EF有最小值，最小值为CE的长. 利用勾股定理求出AD的长，再运用等面积法求出CE的长度即可.

解：如图2，连接CF，CE，

∵在等腰三角形ABC中，AB = AC = 5，BC = 6，AD是△ABC的高，

∴AD垂直平分BC，BD = CD = 3，点B关于AD的对称点是点C，

∴BF = CF，∴BF + EF = CF + EF，

∴当C，E，F三点共线，且CE ⊥ AB时，CF + EF有最小值，即此时BF + EF有最小值，最小值为CE的长.

（作者单位：沈阳市实验学校）

答案：1. 30 2. [48/5] 3. 48