聚焦数学本质，关注数学品格

【教材分析】

本课呈现出各种各样的轮子，引发学生提出轮子为什么设计成圆形的疑问，引出对画圆以及圆的特点的研究，学会画圆、掌握直径与半径的关系，解释轮子做成圆形的原因。本节课是在学生已经初步认识了长方形、正方形、平行四边形、三角形、梯形这些平面图形的基础上进行学习的，为后续圆柱表面积和体积、圆锥体积的计算打下基础。

【教学目标】

1.结合生活实际认识圆，会用圆规画圆，培养规则意识；理解圆心、半径、直径的意义，掌握圆的特征，理解同一个圆（或等圆）里半径与直径的关系，发展空间观念。

2.在探究圆的特征的过程中，培养学生全面思考、细致严谨的思维品质，以及大胆质疑、言必有据的理性精神；在观察、操作、想象、解释等活动中，积累数学活动经验。

3.体验数学与生活的密切联系，从数学的角度感受圆的美，激发爱国主义情感。

【教学重难点】

教学重点：认识圆，在探索中发现圆的特征。

教学难点：通过画圆理解、感悟、发现圆的特征。

【教学准备】

圆形纸片、直尺、圆规、学习任务单等。

【教学过程】

一、创设情境，提供素材

（一）出示情境图，引发思考

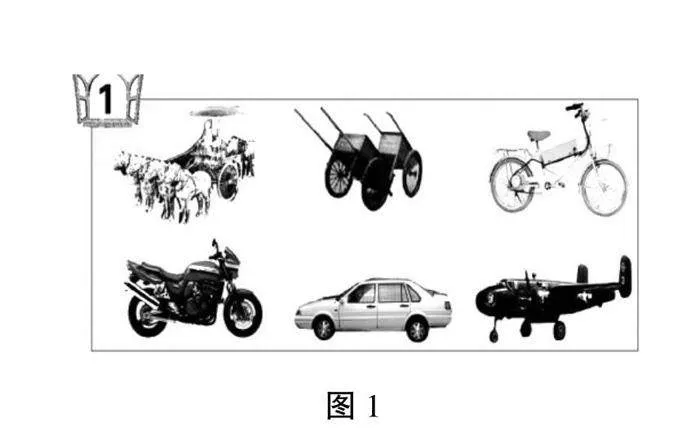
师：随着时代的进步，我们的交通工具也在不断发生着变化，看，你认识它们吗（如图1）？

生：马车、人力车、自行车、摩托车、汽车、飞机。

师：交通工具在变，但有一点没变，你发现了吗？

生：都有轮子，而且轮子都是圆的。

师：深入想一想，轮子为什么是圆的呢？

生1：圆形轮子易于滚动。

生2：圆形轮子滚动起来平稳且不颠簸。

师：大家都有生活体验，那圆和我们之前学习的平面图形有什么不同？

生：长方形、正方形、平行四边形、三角形和梯形，这些图形的边都是直的，圆的边是弯曲的。

师：也就是说，我们以前所学习的平面图形是由线段围成的，而圆形则是由一条曲线围成的平面图形。看来轮子设计成圆形和圆的特点有很大的关系，这节课我们就对圆做进一步的研究。（板书课题）

（二）回顾方法，迁移经验

师：既然都是平面图形，它们在研究方法上就有相同之处。回顾一下，研究长方形、正方形等平面图形时都用到了哪些常用的研究方法？

生：画一画，量一量，折一折。

师：我们把这些方法迁移到今天的学习上，一起探究圆的特征。

【评析】通过创设变化中的交通工具这一情境，激发学生的好奇心和求知欲：车轮为什么要设计成圆形的？学生对所学内容产生了浓厚的兴趣，把潜在的学习欲望变成实际的学习动力，调动学习积极性，使数学课堂充满生机和活力，同时通过回顾之前平面图形的研究方法，实现今天对圆研究方法的迁移。在本环节中，教师一连串的问题引发学生深入思考圆和以前所学的平面图形的不同之处，激发学生探究圆的本质特征的欲望，培养学生独立思考、勇于探索的精神。独立思考与探索精神的培养，不仅有利于优化学生的思维质量，提高创新能力，更能为学生的终身教育蓄养能量。

二、观察操作，研究图形

（一）初次画圆，感受圆是曲线图形

师：既然我们要研究圆，那先画一个圆吧。画在你的学习任务单上。

交流：

生1：我是把杯子盖放在纸上画出来的。

生2：我是用圆规画的。

生3：我把图钉扎在纸上，拉紧绳子画出来的。

师：无论是用什么方法，在画圆的过程中你们是不是进一步体会到圆是由一条曲线围成的平面图形。

（二）二次画圆，体会圆规画圆的普适性

师：你们能用刚才画圆的工具画一个再大一些的圆吗？

学生尝试画圆，讨论交流。

师：老师发现有的同学遇到困难了，说一说你为什么不画了？

生1：用实物比着画，圆的大小是固定的，没法画出更大的圆。

生2：用图钉TYreB6CaZ5LHDAy+Uxf/tyrny0KXY480F5kOXP2Q21I=线绳画，绳子的长度有限，没法画更大的。

师：圆规可以画出大小不同的圆吗？

生：把圆规两脚分开的大些，可以画出一个更大的圆。

师：使用圆规画圆，可以画出大小不同的圆，圆规是我们在纸上画圆的常用工具。

（三）三次画圆，掌握方法，感悟特征

师：我们借助圆规画出一个圆，边画边思考如何能画得又好又快。

师：老师发现这位同学是第一个画完的，并且画得非常好，我们请她来给大家介绍一下方法，好吗？

生：针尖要固定好，圆规叉开的两脚距离不动，旋转一周。

师：这位同学抓住了画圆的关键，画圆时要固定针尖这个点即定点，固定针尖到笔尖的长度即定长，然后旋转。下面我们跟随微课具体来看一下如何运用圆规画圆。

小结：图钉线绳画圆与圆规画圆的道理是一样的。图钉固定的位置就是定点，线绳的长度就是定长，旋转一周就能画出一个圆。生活中我们常用这种方法画圆。

【评析】画圆是本节课的重中之重，由于高年级学生已经具有丰富的生活经验，于是第一次画圆，教师不做任何指导，让学生用自己喜欢的方法画圆，这一环节充分关注学生知识起点的同时，体悟圆作为曲线图形与以前所学的平面图形的不同之处；第二次借助圆规画圆，感受圆规画圆的普适性，在画中反思，归纳出圆规画圆的技巧。这一过程，不仅关注了学生画圆技巧形成的动态过程，还培养了学生反思质疑、实事求是的科学态度。教师将圆规画圆与“钉绳画圆”进行比较，让学生体会不同的画法有着相同的本质，即定点、定长，为后续学习半径及特征打下基础；第三次带着问题画圆，引发学生进一步思考，原来定点决定圆的位置，定长决定圆的大小。教师引导学生用数学的眼光去观察、用数学的思维去分析、用数学的语言去表达，将对画圆的感性认识提升到对圆本质特征的把握，凸显数学的严密性与思想性。

三、引导建构，认识图形

（一）认识圆各部分的名称

1.圆心

师：大家都掌握了圆规画圆的方法，请你们用这种方法再画一个圆，听清要求：新画的圆要和刚才的圆在同一位置上，比刚才的圆小一点。

师：哪位同学到前面来说一说你是怎样画的？

生：找到上次针尖扎的那个点，将圆规两脚间的距离缩短一些，就可以画出来了。

师：通过这次画圆，你又有什么新的发现呢？

生：定点的位置就是圆的位置，定长的长度就能决定圆的大小。

师：老师在黑板上画一个圆，画圆时固定的一点你知道叫什么吗？

生：圆心。

师：圆心通常用字母“O”来表示。

2.半径

师：你能在圆上画一条线段表示圆规两脚间的距离吗？谁愿意到黑板上画一画，其他同学画在学习单上。这样的线段有多少条呢？

生：无数条。

师：你知道这样的线段叫什么吗？

生：半径。

师：仔细观察，半径是一条怎样的线段？

生：一个端点在圆心，另一个端点在曲线上的线段叫半径。

教师在与学生的交流中介绍圆上、圆内、圆外。

师：连接圆心到圆上任意一点的线段叫作半径，一般用字母r来表示。

师：你是怎么理解“圆上任意一点”的？

生：圆上有无数个点。

师：对，圆上有无数个点，每一个点都对应着一条半径，这无数个点也可以看作是由一个点绕圆心旋转得到，这样就形成了一条完美的曲线，这就是我们所说的“点动成线”。

3.直径

师：圆除了圆心、半径还有直径，你们听说过吗？谁能画出圆上的一条直径？还有吗？

师：观察并且思考，直径又是一条怎样的线段呢？

生：从圆上一点到对面圆上一点的线段。

师：这条线段是直径吗？为什么不是？

生：没有过圆心。

师：那直径要满足几个条件？

生：两个，过圆心并且两端都在圆上。

师：正像同学们所说，通过圆心并且两端都在圆上的线段，叫做直径，一般用字母d来表示。

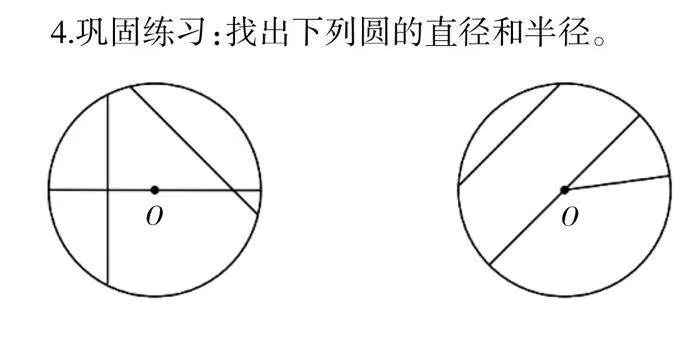
4.巩固练习：找出下列圆的直径和半径。

（二）探索圆的特征

师：同学们，刚才我们认识了圆心、半径和直径，其实圆还蕴藏着许多丰富的特征呢，想不想自己动手来研究？以小组为单位动手折一折、量一量、画一画，并将你的发现记录在学习任务单上。

小组合作探究，全班交流。

生：半径有无数条，长度相等。

师：数学要有理有据，你们是怎样发现的？

生1：画出几条半径，量一量长度。

生2：将圆对折后发现半径完全重合，所以半径有无数条，长度相等。

师：如果不量、不折，怎样知道半径的长度都相等？

生：画圆的时候圆规笔尖到针尖的距离不变，这段距离就是圆的半径，所以半径的长度都相等。

师：你真善于思考，联系刚才画圆的经验得到半径的这一特点。

师：（出示大小不等的两个圆）这两个圆的半径相等吗？在什么情况下才相等？

生：在同一圆内。

师：对，如果不在同一圆内，两个相等的圆这个结论也是成立的。所以我们说“半径都相等”时加上“在同圆或等圆内”这一前提就更加严谨了。

师：对于直径，你们有什么发现？是怎样发现的？

生1：画一画，量一量。

生2：折一折，量一量。

生3：一条直径等于两条半径的长度，半径的长度都相等，所以直径的长度也相等。

师：同一圆内直径和半径的长度有什么关系？怎样简洁地表达它们之间的关系？

生：d=2r，r=d

师：用字母表示，这就是数学的简洁之美。对于圆，你还有其他发现吗？

生：圆是轴对称图形，有无数条对称轴。

师：它的对称轴在哪里？

生：就是它的直径。

师：对称轴是直线，直径是线段，这样说不合适。

生：对称轴是直径所在的直线。

【评析】数学思维是数学教学的灵魂。当学生通过动手操作得出“半径的长度都相等”这一结论时，教师没有急于纠正，而是先引发学生思考、辨析，体会“半径都相等”的结论应该加上“在同圆或等圆内”这一重要前提，有效培养学生表述的准确性和数学思维的缜密性。由于画圆时学生已经积累了足够的感性经验，所以对圆的半径与直径的特点都有感悟。教师将用力点放在引导学生通过画、量、折、比等方法开展验证活动。通过几次追问“你是怎样发现的？”引导学生不仅用动手操作的方法直观发现半径与直径的特征，还通过具有启发性的问题“如果不画、不量、不折，能不能验证？”引导学生用推理证明的方法深刻理解圆的本质特征。

四、巩固新知，拓展应用

师：早在2000多年前，我国伟大的思想家墨子就说过：“圆，一中同长也。”“一中”是什么意思？“同长”呢？

生：一中是指一个圆心，同长是指半径同样长。

师：“一中同长”这四个字高度概括了圆的本质。同一时期《周髀算经》也记载了“圆出于方”，你是怎样理解这四个字的？

生：圆形可以由正方形得到。

通过视频感受“圆出于方”的数学美与极限思想。

师：回顾上课开始的问题，你能运用今天学过的知识解释一下车轮为什么会做成圆形的吗？

生：在同一圆内，半径的长度相等，所以圆形的车轮行驶起来更加平稳。

小结：车轮之所以做成圆形，并使车轴通过圆心，是因为当车轮在地面上滚动时，车轴离开地面的距离总是等于车轮半径那么长，这样行驶起来才会平稳。椭圆形车轮滚起来会怎么样？你能用手比画一下吗？方形车轮呢？

【评析】通过解决课前问题“车轮为什么要设计成圆形的”，使学生体会数学来源于生活又服务于生活的道理，培养学生的问题意思、应用意识。数学有着丰厚的历史沉淀，是先哲智慧的结晶。数学的博大精深有待教师引领学生通过学习去感受，人类的智慧与文明有待教师带领学生去领略。本环节“一中同长”“圆出于方”等数学文化的介绍，从历史的视角去丰富学生原有的认知结构，探寻古老的数学文化与数学极限思想的契合，感受祖先智慧的光辉。

五、总结反思，欣赏拓展

师：一节课很快就要结束了，通过本节课的学习，你有什么收获？

学生从知识、方法、情感三个方面进行回顾。

师：带着这些收获让我们一起回顾本节课的学习过程：通过观察不同时代的交通工具，我们提出了轮子为什么要设计成圆形这一问题，开始了对圆特征的探究；在画圆的过程中我们认识了圆心、半径和直径；通过动手操作研究了圆的特征，明白了轮子做成圆形的科学道理。

师：除了车轮是圆形的，其实圆在我们的生活中无处不在，古希腊哲学家毕达哥拉斯说过：一切平面图形中最美的是圆形。我们一起来欣赏圆的美，希望同学们在生活中做美的发现者、创造者和探究者。

【评析】育人始立美，美育不应成为音乐、美术课的专利。小学数学教学中恰当地渗透美育，将会极大地激发学生对数学的兴趣，让他们感受数学的独特价值。在探索圆特征的过程中，学生通过画、量、折等活动，经历观察、操作、猜想、验证等过程，感受圆的对称美与和谐美。课末欣赏生活中的圆，使学生再次体会圆独特的魅力与数学的美学价值。

总之，教师深刻把握圆概念的本质属性，充分关注学生已有的数学活动经验，设计更加符合学生心理特征的学习活动，让学生积极地参与到教学实践中来，主动经历圆概念本质属性的探索过程，激发学生探究发现的热情，提升学生领悟数学概念的本领。在聚焦数学本质、发展数学能力的同时，蓄养理性精神，历练严谨思维。

（作者单位：青岛杭州路小学）

编辑：温雪莲