基于图神经卷积网络的点云配准算法

摘 要：为了解决现有点云配准算法对配准点云的初始位置或噪声敏感，对独特几何结构的需求以及算法设计复杂、通用性差等问题，本文提出了基于图神经卷积网络的点云配准算法。该算法利用图神经网络在不规则点云图形结构中寻找关键顶点特征，简化原有点云结构，利用在顶点所属对象特征和局部几何信息中学习到的混合特征来构建点对应的分配网络，并提取所需的图特征。同时，通过将模拟配准信息输入另一卷积网络中，计算最佳的配准拟合参数。该算法降低了对配准初始值的依赖，使算法快速收敛，提高了在点云局部可见情况下的配准质量。

关键词：图神经卷积网络；点云；迭代；收敛

中图分类号：P 237 " " " " 文献标志码：A

随着激光雷达（Light Detection and Ranging，LiDAR）、3D体感摄影机（Kinect）等高精度传感器的快速发展以及基于深度学习的点云配准算法的提出，点云已成为表征三维世界的主要数据格式。如何将传感器探测到的有限场景数据组成的点云采用配准算法生成完整的三维场景点云，成为当前的主要问题[1-2]。根据变换矩阵，可以将同一个三维场景或物体的部分扫描点云合并为一个完整的三维点云。

1 点云配准算法现状分析

1.1 基于距离的匹配算法

基于距离的匹配算法包括迭代最近点（Iterative Closest Point，ICP）算法、RPM（Robust Point Matching，RPM）等。ICP算法通过迭代的方式解决点云的刚性配准问题，主要步骤如下。1）基于最近的空间距离寻找hard点的对应关系。2）求解最小二乘变换。其中，步骤1）对配准点云的初始位置和噪声点/离群点敏感，可能导致在迭代的过程中收敛到错误的局部最小值。这类算法对配准点云的初始位置或噪声敏感，因此需要采取措施降低对初始位置和噪声的影响。

1.2 基于特征的匹配算法

一种是基于局部坐标系（LRF）的算法[3]，其中典型的是基于局部特征描述符的旋转图像（Spin Image，SI）。该算法首先将关键点的法向量作为参考轴，其次将局部邻域点投影到以水平和垂直投影距离为坐标的二维平面，最后通过二维累加运算的方式得到1张二维灰度图。这个特征描述符主要依赖采样点的法向量方向，对噪声的鲁棒性较差并且计算复杂度较高。另一种是点特征直方图（PFH）。首先，PFH 描述符采样点和其邻域点的法线和位置差异构建局部坐标系，其次，根据局部坐标系描述两点的局部特征信息，最后，计算所有邻域点两两之间的局部信息并用直方图表示。PFH具有较强的鉴别能力，但是计算耗时较长。为了提高效率，笔者产生了利用简化版点特征直方图（SPFH）来构造快速点特征直方图（FPFH）的思路。FPFH具有快速、鉴别能力强的特点，但是降低了特征维度和通用性。

这类算法要求计算的点云具有独特的几何结构，否则不能有效地进行信息配准。

1.3 基于学习的匹配算法

例如点云配准（PointNetLK）、 深度最近点（DCP）以及PRNet等。PointNetLK将LK算法和PointNet融合到一个单一的可训练的递归神经网络中，具有较好的泛化能力和高效的计算能力。但是它主要用于局部到整体的配准变换，需要主体模板。DCP是局部到局部的配准算法，通过一种基于注意力机制的深度神经网络模型（Transformer）中的注意力机制计算出1个“假想的目标点云”。这个假想的目标点云与待调整点云之间点的对应关系已知（soft matching：使用一种概率方法来生成从一个点云到另一个点云的“软映射”）。再通过损失函数约束，间接使假想的目标点云向真正的目标点云不断逼近，最终实现点云的对齐匹配。但是DCP的收敛性不高，在计算中多次使用软映射，导致计算过程较复杂。这类算法大多基于整体特征的提取，不能有效地解决局部到局部的点云匹配问题。同时，算法设计复杂，无法在较短的时间内得到理想的结果。综上所述，现有的配准算法大多通过对应搜索和变换估计2个过程来缩小几何投影误差。这2个过程交替进行，直到几何重投影误差最小。在已知精确对应的情况下，变换估计有一个闭环形式的解[4]。

2 解决方案

针对点云配准的现状，本文提出一种有效的图神经卷积网络。该网络从局部到局部的微分网络保留基于距离匹配算法中对离群点的鲁棒性，同时训练得出所属对象特征中的对应关系，减少对初始值的依赖。具体实施步骤如下。

步骤1：将原始输入的点云命名为X点云数据，将目标点云命名为Y点云数据。在X中，将N个点组成的点云数据定义为一个集合P={p1，…，pN}，其中每个元素pi=（xi，si）。这里，xi为三维坐标系中该点的坐标，si为点属性的k维度向量，这个值包括自身与周围点的信息以及自身的位姿信息和条件信息。给定点云P，使用此点云P作为1个顶点Pi，此时X点云数据就变为1个少量的点云集合I={P1，……，Pn}。

步骤2：对减少后的点云集合I使用FPS最远点采样方法（采用欧几里得距离度量点之间最远距离）。在对第一个点采样的过程中，可以随机从数据中选取1个点，或者求整个数据点（点云）的重心（即所有点坐标求和平均得到的坐标点），选取距离重心最远的点为初始采样点，记为K0。继续选取剩余的所有点中距离初始采样点最远的点，记为K1。对剩下的每个点，分别计算其到K0和K1的距离，并选取距离最小的点作为这个点到K0和K1整体的距离。完成这些距离的计算后，选择距离最大的点，记为K2。重复以上操作，最终取到所需的M个点。根据M个点的特征，概括稠密点云特征，最后进行编码，将其概括为顶点的初始状态si1（表示初始点云所有顶点经过第一次计算后得到的Si）。利用体素滤波再次减少点的数量，然后使用3D稀疏卷积进行特征提取，确立最终的顶点点云数据集合P。在集合中，每个点Pi利用固定的半径r寻找另一个相邻顶点Pj进行连线E，构建图形Gx=（P，E），其中E={（Pi，Pj）| ||xi-xj||2lt; r}。

步骤3：对图形G使用图神经网络（GNN）细化顶点状态进行配准特征提取。这里采用邻接表表达图的关联性，如果采用邻接矩阵，其多表示性（指多种邻接矩阵表示一种连通性）就会导致细化结果不准确，从而影响后续的操作。采用顶点间的相对坐标作为输入，同时根据相邻的顶点结构特征调整坐标，计算得到每个顶点的不同特征信息。如公式（1）所示。

sit+1=gt（ρ（{f（xj-xi+∆xit，sjt）}），sjt） " " " " " "（1）

式中：t为迭代次数；xj为三维坐标系中与Pi相邻点Pj的坐标；sj为与Pi相邻点Pj的属性的k维度向量，这个值是自身与周围点的信息以及自身的位姿信息和条件信息；ρ（…）为聚合每个顶点边要素的函数集合；gt（…）为利用聚合的边特征跟新顶点特征的函数；f（…）为输入变换幅度，用于减少平移和变换造成的特征差异；∆xit为顶点要配准的偏移量大小，由公式ht­（…）决定。

使用多层感知器（MLP）对这些函数进行建模输出。在输出过程中，引入添加残差结构以消除∆x在计算过程中产生的偏移误差。值得注意的是，每个迭代次数t都使用不同的MLP，即每次迭代并不共享MLP。

步骤4：将经过迭代计算后的属性向量特征si写入顶点的元素向量Pi中。同时，为了提高鲁棒性，本文将ρ（…）设置为Max聚类。在完成t次迭代的图神经网络中，使用顶点状态值来预测初步的特征，并对这些特征进行归一化处理，以生成所需的图特征Ux。

步骤5：对Y点云数据进行随机的平移、翻转等变换，并将此时的变换状态记作σ，然后对变换后的Y点云数据按照上述X点云数据的处理方式，求出所需的图特征Uy。

步骤6：通过上述步骤，确定了2个图特征Ux和Uy、它们构成的图形Gx和Gy以及点集I和连线E。将X、Y的点云数据进行标记，并通过通道数模式叠加（即使用concat链接）。然后，通过一个共享参数的MLP结构网络，并使用最大池化层进行归一化和维度缩减，得到所需的2组关联性结果数据α和β。为了确保数值为正，使用leaky_relu作为激活函数。如公式（2）所示。

∆xit=MLPht（sit） （2）

式中：MLPht为t层感知机网络。

步骤7：根据关联性结果数据，并结合基础数据，计算X与Y点云之间的相关性，如公式（3）所示。

（3）

式中：nKC为点与点云核之间的相关度；Qi为目标点云的点；Pi为输入点云对应Qi的点；|E（Qi）|为根据Y点云数据建立的图Gy中求出的关于i的E中所有的点的个数；len（E）为根据Y点云数据建立的图Gy中求出的关于i的E中所有的边的个数；m为当前求和步骤中目标点云的Q点在图Gy中对应的边；n为当前求和步骤中作为对象被分析的点，其属于E（Qi）域；E（Qi）为根据Y点云数据建立的图Gy中求出的关于i的E中所有的点；sn为与Pi相邻点Pj的属性的k维度向量；Kσ（…）为构建核的函数，是高斯函数一种公式，通过相关度⊙点乘参数，扩大顶点之间相关度关系，完成对X、Y点云数据的相关性特征的编码提取。如公式（4）所示。

（4）

步骤8：进行奇异值分解（Singular Value Decomposition，SVD）以求解位姿问题。对给定的2个待配准点云X和Y，其中P为源点云，Q为源点云经过变换后的目标点云，三维点云配准任务为寻找合适的变换参数即旋转矩阵R和平移向量T，使配准后的点云在同一坐标系下对齐。在确定点云之间的对应关系后，变换参数可以通过优化以下目标函数来求得，如公式（5）所示。

（5）

式中：O为函数名；N为整个点云的数量。

在配准过程中，不是所有的点都有一一对应的关系，设置一个权重ωi，增加数据的可用性，减少因为强制匹配产生的错误配准。

使用SVD求解配准变换参数的计算步骤如下：通过下列公式分别计算源点云和目标点云的质心，即求取点云中点的均值，如公式（6）所示。

（6）

式中：N1为点集I中顶点的数量。

求解点云的协方差矩阵H，如公式（7）所示。

（7）

对协方差矩阵H进行SVD分解，如公式（8）所示。

[U，S，V]=SVD（H） " " " "（8）

式中：U、S、V分别为进行SVD分解后得到的降维矩阵的均值、方差与中心矩阵。

求解旋转矩阵R和平移向量T，如公式（9）、公式（10）所示。

R=VUT " " " " " " " （9）

T=-R·+ " " " " "（10）

解算出初始变换矩阵后，将其应用于源点云得到初始配准结果。由于点云位姿变换具有复杂性，神经网络难以一次性地对配准参数进行精确估计，因此利用RANSAC算法（随机抽样一致算法，这是一种通用且非常成功的估计算法，它能够应付大比例野值的情况）的方法迭代将变换后的源点云与目标点云重新输入网络计算，使配准误差不断变小，直到达到最大迭代次数或两次产生的矩阵之差小于阈值，点云精细配准过程如公式（11）所示。

（11）

式中：Rl为最终旋转矩阵；T l为利用RANSAC算法估算后的平移向量。

步骤9：定义Loss函数，在点的分类判断中，1个顶点在1个对象的框中，笔者将对象值赋给这个顶点。如果1个顶点位于任何边界框之外，则它属于背景类。笔者用平均交叉熵损失作为分类损失，如公式（12）所示。

（12）

式中：Lcls为平均交叉熵损失；yi cj为第i个点的真实概率；Pi cj为

第i个顶点的预测概率。

根据变换矩阵网络设计2个损失函数：Lreg和Lest进行迭代传送，并独立计算，使预测配准参数与真实配准参数之间误差最小，如公式（13）～公式（15）所示。

（13）

式中：I为点云内的比例系数；Rgt为真实变换矩阵；tgt为真实平移向量值；Rpred为网络估计的变换矩阵；tpred网络估计的平移向量值。

Lest=||（Rpred）-1·Rgt-E4|| " " " " " " " " " " " " （14）

式中：E4为Rpred与Rgt相等时的单位阵。

Lt=Lreg+λLest " " " " （15）

式中：Lt为两类损失加权求和得到的损失值；λ为权值。

考虑每次迭代的损失，将损失设置为每次迭代损失的加权和并且每次迭代都是独立的，确保最终得到的R、T结果预测值符合真实值。如公式（16）所示。

（16）

式中：L为总体的配准损失；N为总迭代次数；i为当前迭代数；Lti为第i次迭代产生的损失值。

3 本点云配准算法优势

3.1 特征筛选与点云量化改进

步骤1～4利用图神经网络中的点与临近点之间的关系以及自身的位姿信息和条件信息等筛选特征，建立顶点之间的相关性信息。并结合网格绘制（gird-based）和点绘制（point-based）在量化点云的同时使特征被赋予更良好的定位信息，使网络能更好、更快地提取特征信息。

3.2 滤波与平移误差优化

步骤5、步骤6利用初步统计和拟合信息，创建初步的滤波和确定平移误差，并通过残差网络链接至后续的变换网络中，加速计算并使计算结果更方便、准确。

3.3 高斯方程求解与预测变换优化

步骤7、步骤8将计算结果与KC（核相关）算法结合，建立核相关高斯方程，通过密度估计相关性和图形点之间对应关系求解预测变换的R、T值，不断迭代更新直至2次产生的矩阵之差小于阈值，完成预测。

3.4 创立新Loss函数

步骤9创立了新的Loss函数链接预测值和正值，迭代更新且保持迭代的独立性，完成点云配准变换。

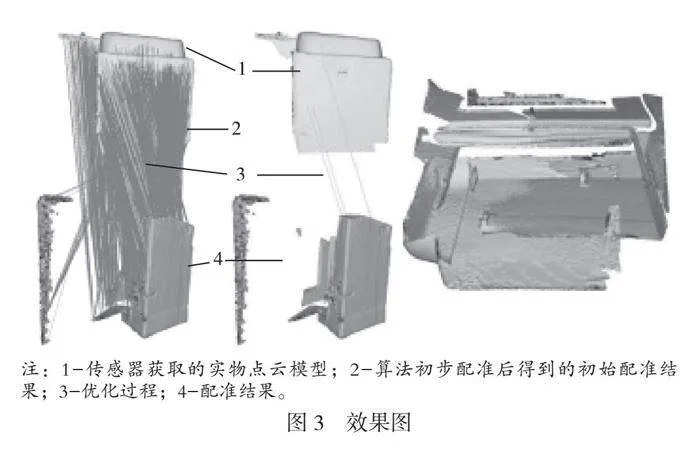
4 效果展示

该算法利用图神经网络考虑点与临近点之间的关系，结合自身的位姿信息和条件信息筛选特征。从而降低了对配准初始值的敏感度，并减少了异常点对算法结果的影响。在存在异常点输入的情况下（如图1所示），该算法仍能够输出较为准确的配准结果（如图2所示）。

图3为该算法的配准过程模型图，该过程将持续进行，直到达到最大迭代次数，或者某次迭代与前一次迭代产生的矩阵之差小于预设阈值，最终得到精确化的配准模型。

5 结语

截至2023年底，基于距离的匹配算法仍然容易受到噪声的干扰，而基于特征的匹配算法则要求计算的点云具有独特的几何结构，否则无法有效地进行信息配准。与此同时，基于学习的匹配算法较为复杂且收敛性较差。基于图神经卷积网络的点云配准算法则利用点与邻近点之间的关系简化了点云的结构，确立了顶点间的相关性，同时提供了更准确的定位信息。在配准计算中，该算法通过残差网络加快了计算过程，并得到了更精确的R、T结果。与KC算法的结合使其在迭代更新中计算出的矩阵差值能够收敛于阈值内，同时保证了每轮迭代的独立性。最终，该算法能够完成点云配准变换，为相关领域的研究和应用提供了有力的支持。

参考文献

[1]杨必胜，董震.点云智能研究进展与趋势[J].测绘学报，2019，48（12）：1575.

[2]王畅，舒勤，杨赟秀，等.利用结构特征的点云快速配准算法[J].光学学报，2018，38（9）： 175.

[3]耿国华，刘晓宁，周明全.基于局部坐标系和哈希技术的空间曲线匹配算法[J].计算机工程， 2003， 29（4）：3.

[4]GUO Y，WANG H，HU Q，et al.Deep learning for 3d point clouds：

A survey[J].IEEE transactions on pattern analysis and machine intelligence，

2020，43（12）：4338.