基于深度强化学习的城市公共交通票价优化模型构建

摘 要：本文介绍了一种基于深度强化学习的城市公共交通票价优化模型，构建该模型的目的在于提高城市交通系统的效率和服务质量。首先，分析了该模型的基本假设和建立过程。其次，探讨了使用DQN方法对模型进行训练和优化的过程，最后，该文展示了持续监测系统性能、乘客数量、收入和交通拥堵情况等票价模型的优化结果，以期为城市公共交通系统的管理和改进提供一种前瞻性方法。

关键词：深度强化学习；城市公交；票价优化模型

中图分类号：U-9 " " " " " " " 文献标志码：A

随着城市化的快速发展，公共交通成为减少城市交通拥堵、减少污染、提高居民生活质量的关键组成部分[1]。而公共交通票价策略是管理城市公共交通系统的关键因素之一，合理的票价策略不仅可以吸引更多乘客乘坐公共交通，还可以提高运营效益，减少拥堵，降低碳排放。基于此背景，深度强化学习（Deep Reinforcement Learning，DRL）应运而生。DRL结合深度学习和强化学习的技术，能够使系统在与环境的互动中学习并适应最佳策略。本文的目标是开发一种基于DRL的城市公共交通票价优化模型，该文将详细介绍基于深度强化学习的城市公共交通票价优化模型的构建和训练过程，通过模拟和学习，使模型能够自主决策最佳票价策略，有望为城市交通管理者提供一个灵活、自适应的工具，以优化票价策略，提高乘客体验，降低交通拥堵，并最大化运营收益。

1 城市公共交通票价优化模型

1.1 基本假设模型

假设城市公共交通市场存在一定数量的潜在乘客，那么这些乘客具有出行需求，前往不同的目的地、出行时间和距离各不相同[2]。这个需求可以根据不同地点和时间段而变化，形成一个动态的需求曲线。而市场中存在一定数量的公交车、地铁列车等交通资源，用于满足潜在乘客的出行需求，这些资源在不同线路和时段提供不同的服务。根据乘客的出行需求选择使用公共交通，而交通资源会根据需求提供相应的服务。因此，需求与供给之间存在一定的匹配关系，交通资源的利用率会受到乘客需求的影响。在模型中，假设市场存在私人汽车、出租车以及共享单车等多种出行方式，这些方式会构成城市公共交通的竞争或替代。当乘客出行时，会考虑这些替代方式，根据其特点和成本来选择最适合自己的方式。同时，票价是乘客出行选择的一个重要因素，当其他出行方式提供相似的服务时，公共交通的票价策略可能会影响乘客的选择。因此，模型需要考虑在竞争环境下的票价策略，以吸引乘客选择公共交通方式。当乘客选择出行方式时会综合考虑票价、出行时间以及便捷性等方面，而模型需要考虑这些因素来制定具有竞争力的票价策略。

1.2 模型建立

在模型建立的过程中，对状态空间的定义、动作空间的设定以及奖励函数的设计等要素都是构成深度强化学习模型的核心[3]。模型的状态空间包括城市的不同交通线路、不同时段、天气情况以及乘客需求等多个因素。状态空间可以表示为S={s1，s2，...，sn}，其中每个sn表示一个状态因子，例如，s1表示线路，s2表示时段，s3表示天气等。动作空间（Action Space）包括不同线路或时段的票价设定，其可以表示为A={a1，a2，a3，.....am}，其中每个am表示一个票价策略，例如，a1表示提价Δp1%，a2表示降价Δp2%，以此类推。此外，建立模型设置奖励函数，用于评估模型每个动作的好坏，其主要影响模型的学习和决策过程。奖励函数R（s，a）考虑多个因素，如乘客数量、收入以及交通拥堵情况等，如公式（1）所示。

R（s，a）=ζ·（pinewci）·qi " " " " " " " " " " " " （1）

式中：ζ为奖励系数；pinew为新的票价；ci为单位成本；qi为出行需求。

此外，建立模型还需要构建一个虚拟环境，以模拟乘客的行为、交通流量以及票价策略的影响等。这个模型将与深度强化学习代理进行互动，提供有关城市交通系统的反馈信息。深度强化学习代理将使用神经网络Q（S，A）来表示价值函数，其中S表示状态空间，A表示动作空间。价值函数表示了在给定状态下采取某个动作的预期回报。模型将基于贝尔曼方程来更新Q值，以逐步优化策略。

2 基于深度强化学习票价优化模型训练

2.1 DQN法训练

在基于深度强化学习的票价优化模型中，该文主要采用了深度Q网络（Deep Q-Network，DQN）来进行模型训练[4]。DQN是一种强化学习算法，用于训练智能代理以学习最佳的决策策略。DQN法训练的核心思想是使用深度神经网络来估计每个状态-动作对的价值函数，以便选择最佳的行动。具体步骤如下：1）神经网络的输入是状态空间的表示，输出是每个动作的Q值估计。神经网络结构包括输入层、隐藏层和输出层。输入层接收状态空间的表示，描述城市交通系统当前状态的信息，每个状态因子都被编码为网络的输入节点，这些输入节点构成状态向量，作为神经网络的输入。隐藏层是神经网络的核心，包括多个神经元节点，用于处理输入数据并提取特征。隐藏层通过学习权重和偏差来逐步优化状态-动作对的Q值估计。输出层的节点数等于动作空间的大小，每个节点对应一个不同的票价策略。输出层的值表示每个动作对应的Q值估计。而神经网络的训练目标就是使输出层的Q值逼近真实的最优Q值。2）在神经网络结构的基础上估计Q值，对于每个状态-动作对（s，a），将状态s作为输入，通过前向传播计算神经网络的输出，即预测的Q值，表示为Q（s，a）。这个预测的Q值估计是基于模型学到的知识来估计在状态s下采取动作a的长期回报。在训练阶段，神经网络会通过与环境的互动来不断调整其参数，以更准确地估计Q值。模型会根据当前策略选择动作a，进入下一个状态s'，并观察获得的即时奖励R（s，a）。3）用贝尔曼方程用于更新Q值，计算模型当前预测的Q值和目标Q值之间的误差，逐步优化模型的决策策略。具体更新如公式（2）所示。

Q（s，a）=Q（s，a）+a[R（s，a）+γ·max（Q（s'，a'））-Q（s，a）] （2）

式中：α为学习率，控制每次更新的幅度。R（s，a）为采取动作a后在状态s下获得的即时奖励。γ为折扣因子，代表未来奖励的重要性。s'为下一个状态，a'为在下一个状态下选择的最佳动作。该预估公式主要利用误差进行反向传播，调整神经网络的权重和参数，使预测的Q值逐渐逼近目标Q值。此步骤允许模型不断更新Q值，以更准确地估计每个动作的长期回报，从而指导模型选择最佳的票价策略。

总之，DQN法的训练过程是一个迭代的过程，模型不断尝试不同的动作并观察奖励，以学习如何制定最佳的票价策略。通过该过程，模型可以优化城市公共交通系统的票价，以满足乘客需求并最大化运营效益。

2.2 优化模型

为了提高模型训练的稳定性，可使用经验回放技术观察模型的状态、动作、奖励和下一个状态的数据点存储在一个经验缓冲区中，然后随机抽样这些经验数据来构建训练批次[5]。主要技术要点如下。在每个时间t，将当前状态st、采取的动作at、获得的即时奖励rt和下一个状态s{t+1}组成如下经验元祖。

这些经验元组将被存储在一个经验池中，而经验池的大小通常是有限的，较大的经验池可以存储更多的经验元组，但也需要更多的内存空间。在训练过程中，从经验池中随机抽样一批数据，通常包括N个经验元组，其中N是抽样的批次大小。随机抽样可打破数据的时间相关性，提高训练的稳定性。由于经验池包括了之前的经验，因此模型可以在不同的状态和时间步上进行训练，而不仅是在连续的时间步上。对于每个抽样的经验元组（st，at，rt，s{t+1}），采用公式（4）计算更新Q值。

（3）

式中：Qt表示目标Q值，即更新的Q值；rt表示即时奖励，即在状态st下采取动作at后获得的奖励；γ表示折扣因子，代表未来奖励的重要性；max（Qtnext）表示下一个状态s{t+1}中可选动作的最大Q值。这个目标Q值Qt用于计算Q网络的损失，通常采用均方误差损失，计算过程如公式（5）所示。

（4）

式中：Qt表示目标Q值，即通过贝尔曼方程计算得到的目标值；Q（s，a）表示模型估计的Q值，即模型在状态s下采取动作a的估计值。通过调整模型参数可优化这个损失函数，使模型估计的Q值逐渐逼近目标Q值。在深度强化学习中，通常使用梯度下降或其变种来优化MS损失，通过反向传播算法来更新神经网络的参数，以提高模型的性能。

3 票价模型优化结果

乘客数量是监测模型优化的关键指标，可以用于评估模型的效用。跟踪不同线路和时段的乘客数量，并与模型的票价策略进行对比。具体结果如图1所示。

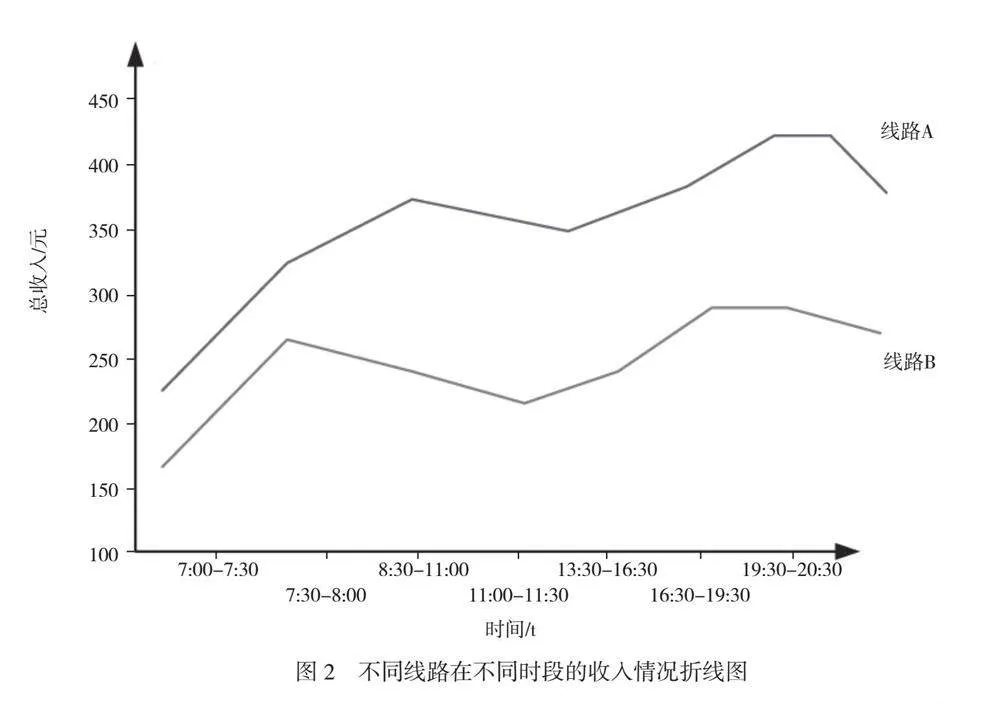
由图1可知，在所有时段中，线路A的乘客数量都明显高于线路B。这表明线路A在吸引乘客方面表现更好。在早高峰和晚高峰时段，乘客数量相对较高，而在非高峰时段，乘客数量较低。这符合通常的交通模式，乘客更容易在高峰时段使用公共交通工具。如果模型的票价策略能够成功地吸引更多的乘客，那么乘客数量值可能会上升，这表明模型的优化结果在增加乘客数量方面取得了成功。收入是城市公共交通系统的重要经济指标，模型的优化应该能够平衡提高乘客数量和增加收入之间的关系。具体结果如图2所示。

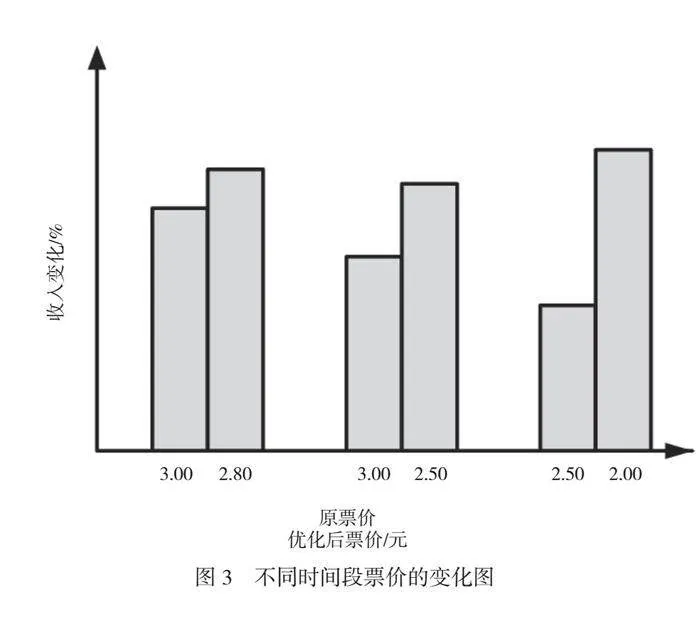
由图2可知，在给定的时段下，线路A的总收入明显高于线路B。早高峰时段，线路A的总收入最高为450元，而线路B的最高总收入为300元。对每个线路在不同时段的收入进行比较，可以看到在07：00—08：00早高峰时段收入最高，在08：30—11：00非高峰时段的收入较低。这种时段间的差异可能受到乘客数量和需求的影响。线路A和线路B在各时段的收入都不同。这表明不同线路的乘客数量和票价策略可能有差异，导致2个线路的收入不同。城市公共交通原票价、优化后票价以及由此带来的收入变化，都反映了模型优化对城市公共交通系统的影响，原票价代表了在模型介入前的公共交通票价水平。这些价格通常根据市场需求、运营成本和其他因素设定。优化后票价反映了深度强化学习模型在考虑乘客需求、交通拥堵情况和城市经济状况等多个因素后，对票价策略进行调整后的结果，这些调整可以包括提价或降价，具体取决于线路和时段的情况。通过观察收入变化，可以判断模型的票价策略是否在经济上有效。具体结果如图3所示。

由图3可知，大多数情况下，模型的优化导致了票价的降价或提价变化。这种变化可能会影响乘客数量和城市公共交通的收入。在优化票价后，交通收入的变化是呈正值趋势增长的，这表示模型的优化策略在经济上是有效的。在不同时段的票价优化结果不同。在早高峰时段，模型降低了票价，导致乘客数量上升，在晚高峰时段，模型提高票价，但仍然提高了收入。总的来说，模型的票价优化策略在不同线路和时段表现了灵活性和适应性，有助于提高收入并在某些情况下减轻交通拥堵。这对于城市公共交通系统的可持续发展非常重要。

4 结语

城市公共交通票价策略对于减少交通拥堵、提高居民生活质量以及降低环境污染具有重要影响，本文结合深度学习技术，研究构建一种基于深度强化学习的城市公共交通票价优化模型，用于优化城市公共交通的票价策略，同时在训练该模型的过程中采用DQN法训练，不断更新模型的Q值，以更好地估计最佳策略，提高模型训练的稳定性。通过本文的研究，希望提高乘客体验，减轻交通拥堵，最大程度地提升城市公共交通的运营收益。

参考文献

[1]李雪岩，张汉坤，李静，等.基于深度强化学习的城市公共交通票价优化模型[J].管理工程学报，2022，36（6）：12.

[2]郑欣宇，毛俊，弓埔政，等.地铁共线公交线路的优化调整方法研究——以大连地铁二号线为例[J].内江科技，2022，43（10）：41-42.

[3]周杰.智慧城市轨道交通发展模型的构建及其发展趋势探讨[J].城市轨道交通研究，2023，26（6）：7-11.

[4]钟力文.一种基于DQN模型提取交通信号配时决策树的方法：CN202310189392.X[P].2023-10-16.

[5]李兰鹏.基于蚁群算法的城市轨道交通列车节能运行优化模型仿真分析[J].城市轨道交通研究，2023，26（2）：11-15.