可再生能源条件下配电网重构研究

摘 要：可再生能源的不断发展使其成为解决气候变化和能源安全问题的重要路径之一。本文目的是分析在可再生能源存在的情况下配电网每小时重新配置的意义。为此，本文设计了一套数学模型，通过每小时重新配置来最大限度地减少每日电网能量损失。该模型是一个混合整数二阶锥规划问题，通过求解器求解。本文考虑了一天中电力需求的变化和可再生能源发电量的波动，将该方法应用于总线系统，并讨论了包括关键参数灵敏度分析在内的结果。

关键词：可再生能源；配电网重构；潮流计算；成本考量

中图分类号：TM 73" " " " " 文献标志码：A

可再生能源的特殊性，尤其是太阳能和风能的不稳定性和间歇性，给电力系统的带来了新挑战。传统电网结构面临可再生能源接入的难题，产生了各种电压不稳定、频率波动等问题。因此，在可再生能源条件下进行配电网重构研究，实现电力系统的可持续发展和稳定运行越发重要。本文考虑了小时负荷的变化、可再生能源发电的波动以及切换成本，对提高可再生能源发电的配电网（DN）每小时重新配置以减少潜在损耗进行了全面评估。

1 系统设计

1.1 总体分析

配电网（DN）重构问题是一个高度复杂的组合问题，是一个混合整数非线性优化问题。可再生能源条件下的配电网重构主要是在大规模接入可再生能源的情况下，对传统的配电网进行调整和改造，以更好地适应可再生能源的高波动性和间歇性特点。

到目前为止，文献中已经应用了大量算法来解决这个问题，可以分为4组，即混合启发式和优化、单独启发式、元启发式和数学方法[1-2]。除数学方法外的所有方法都不能保证取得最优解。使用优化分解方法可解决重构问题。该问题被划分为主级和从级。建模为混合整数非线性规划问题（MINLP）的主级确定了开关的状态，为非线性规划问题的从级验证了解决方案的可行性，这2个阶段使用线性折弯机切割连接。有研究提出3个凸模型，即二次规划（QP）、二次约束规划（QCP）和二阶锥规划（SOCP）来解决重构问题。QP模型在处理时间上是有效的，也给出了相对良好的解决方案，而SOCP模型在更多的处理时间下可以获得更好的解决方案。运用广泛的另外一种混合整数线性规划（MILP）模型估算了线路电流和母线电压的平方值，并用分段线性函数代替。解决方案的准确性取决于工件的数量，缺点是没有评估整体重组是否有益[3-5]。

1.2 潮流方程

潮流计算是电力系统配电网重构研究中的重要部分，主要用于计算电力系统中各节点的电压相位、幅值以及各支路上的功率流向，并及时处理潜在问题，保障电力系统安全、稳定运行

首先，潮流计算通常基于潮流方程。作为一组非线性方程，潮流方程由有功功率平衡方程和无功功率平衡方程组成，描述了电力系统中各节点间的电压和功率关系，需要通过不断迭代计算才能得到稳定的解。其次，潮流计算是电力系统分析中的核心内容，能帮助研究者更好地了解系统的运行情况，并计算系统中各节点的电压和功率，以便做出正确的决策并采取相应的调控措施，保障电力系统的安全、稳定运行。

进行潮流计算时，需要考虑各节点的电压幅值、导纳、相角以及各支路的阻抗等参数，并考虑负载水平、发电机输出等因素。通过潮流计算，可得到系统中每个节点的电压情况，最后判断系统中是否存在电压不稳定、过载等问题，并采取相应的措施进行调整。潮流计算结果对电网的稳定运行和电能质量的保障至关重要。配电网（DN）的功率流通常使用总线注入模型进行建模。该模型含节点变量，如总线电压和功率注入。潮流计算在电力系统规划、运行和故障处理等方面都具有重要作用。通过对系统进行潮流计算，可有效评估系统的运行状况，指导电网的规划建设。支路流量模型侧重于流经支路的电流和功率。无任何损耗的分支流模型的一般形式分别如公式（1）～公式（3）所示。

Vm-Vn=ZmnImn，（m，n）∈E （1）

Smn=VmIm*n，（m，n）∈E （2）

（3）

式中：Vm为线路m处的电压相量；Zmn为线路mn两点阻抗；Imn为线路mn两点间的电流相量；Smn为线路mn间的视在功率；Im*n为Imn共轭复数；E为一组线路；Slm为线路lm间的视在功率；Zlm为线路lm两点阻抗；Ilm为线路lm的间电流相量；Ym*为线路m处对地分流导纳的共轭复数；K为线路组合。

公式（1）满足欧姆定律，支路功率流通过公式（2）进行计算，公式（3）表示所有总线处的功率平衡约束。通过在上述公式中消除电压和电流的相位角，可得到分支流模型的功率公式，分别如公式（4）～公式（6）所示。

（4）

vn=vm-2（RmnPmn+XmnQmn）+（R2mn+X2mn）imn （5）

（6）

式中：PGm为线路m处的有功功率；PDm为线路m处的有功功率需求；Pmn为线路mn两点有功功率；Plm线路lm间有功功率；Rlm为线路lm电阻；Ilm为线路lm间电流有效值；Gm为线路m处电导；vm为线路m处电压幅值的平方；vn为线路n处电压幅值的平方；QGm为线路m处的无功功率；QDm为线路m处的无功功率需求；Qmn为线路mn两点无功功率；Qlm为线路lm无功功率；Xlm为线路lm电抗；Bm为线路m处电纳；imn为线路mn两点间电流的平方。

这种公式被称为DistFlow方程。鉴于非线性等式约束，即公式（6），DistFlow公式是非凸的，为了使模型呈凸性，可以放宽到不等式约束，如公式（7）所示。

（7）

用公式（7）代替公式（6），可利用配电潮流的二次曲线算法。二次曲线公式的主要优点是其为凸性，可确保全局最优解。如果所有不等式约束（公式（7））都收敛到等式约束（公式（6）），那么具有角度松弛的最优潮流的解对于径向DN总是精确的，并且具有圆锥松弛的最优功率流的解为精确的解。

1.3 公式重构

为了对每小时的配电网重新配置进行建模，应修改重新配置模型，以便考虑每小时的负荷和发电量变化。为此，每小时应分别考虑所有约束条件，即维数乘以重新配置小时数。实践中既不考虑切换动作的成本，也不考虑其数量的限制，就能独立获得每小时最优配置。然而，通过限制切换动作的最大数量，或通过在目标函数中考虑切换动作的损失成本来减少切换动作是必要的。在2种策略中，切换动作的数量必须是已知的，切换操作次数的计算方法分别如公式（8）～公式（10）所示。

χmn，h≥αmn，h-αmn，h-1，（m，n）∈E，h∈T （8）

χmn，h≥αmn，h-1-αmn，h，（m，n）∈E，h∈T （9）

（10）

式中：αmn，h表示连接母线m和n的线路在h小时的状态。如果线路的状态从时间h-1变为h，χmn，h则变为1；NS表示进行的切换操作的总数。

现在可以制定切换动作的链接约束。如上所述，可以利用2种不同策略来建立配置小时问题间的联系。第一种策略是对切换操作的最大数量设置上限，可以通过在公式中添加公式（8）～公式（10）来完成，可得NS≤NSmax（NSmax表示最大切换操作次数）、（表示小时重构数学模型）。第二种方法是考虑切换动作的惩罚成本，并将其整合到目标函数中，可以将公式（8）～公式（10）添加到问题中，并用（closs为单位能量损失成本，csw为单位切换操作成本）来实现。

考虑NS≤NSmax和，防止出现对配电网络损耗无影响或影响可忽略的切换动作。这些约束在连续几个小时内建立DN配置间的链接，2个表达式都可避免频繁的切换操作。将NS≤NSmax施加的上限作为一个硬约束，限制切换动作的总数，使模型消除利润较低的重新配置。此外，在与切换动作相关的成本和它们的利润间进行折衷，消除了无益的操作。

1.4 编目构造分析

编码建议包括在类似于编码的矢量中对电气系统的分支进行编码。在该编码中，对于总线nb和分支nl的系统，前（nb-1）元素表示径向拓扑中的分支，其被定义为N1集合，而其他（nl-nb+1）元素表示连接分支，并被定义为集合N2，p为2个集合间的分离点。

使用这种编码可以生成仅由径向拓扑形成的初始种群，并使重组和突变算子从初始种群中的径向拓扑生成新的径向拓扑。很明显，编码方案的解码过程是琐碎的，因为径向拓扑已经由N1的元素形成。本文使用总线测试系统拓扑结构，必须注意的是，在编目中，第一个（nb-1）分支对应树中的分支，其余的（nl-nb+1）分支对应连接分支。还必须注意到分支在2个子群A和B中的排序顺序是无关的。

该编码提案可保证如果初始种群由径向配置组成，就有可能开发重组和突变算子，以在生成的后代中保留径向拓扑。这一协同建议和实现的重组是本文的主要亮点，因为它们消除了非径向拓扑的生成，并允许以类似于自然遗传重组的方式生成后代。

1.5 局部改进

重组后产生的后代进入局部改进阶段。这一步骤实现了算法推广中导出的启发式算法。该策略包括连续检查系统中存在的所有可能的环路，如果找到更好的拓扑，就替换当前拓扑。由于每个环路中存在较低电压，因此需要对支路进行排序，排序的第一个环路是在其任何终端总线中具有较低电压的环路。每个回路中的分支也按照这样的方式排序，即连接到具有较低电压的总线的分支最先被排序。对于每个环路，模拟连接支路和环路中每个支路间的切换。当在循环的两侧发现质量比当前拓扑质量差的拓扑时，该过程停止。如果找到更好的拓扑，将其替换当前拓扑且该过程必须重新开始，以识别剩余连接交换机形成的新环路和每个环路中分支的新顺序。

局部改进步骤包括以下5步。1）生成的子代被转换为当前拓扑，并被认为是局部改进步骤的现任者。2）识别所有连接支路（径向配置之外的支路，原因是它们闭合了一个回路）的2个极端电压。3）根据任何极端电压较低的连接支路对回路进行分类。4）对要分析的回路内部的分支进行排序：第一组要分析的分支形成从电压较低的终端总线到变电站的路径的分支，第二组形成从另一个终端总线到变电所的路径的支路。5）模拟将连接分支替换为每组（循环两侧）循环中的分支而创建的所有邻居拓扑。发现质量比当前任职者差的拓扑时，或者分析所有分支时，该过程停止。如果在循环的模拟中发现了更好的拓扑，就将其替换当前的拓扑，并返回到步骤2，以分析下一个循环。否则，在分析当前拓扑中的所有循环后，局部改进步骤结束。

现任者代表改良后的后代，但在将其引入群之前，有必要验证其可行性，并相应地进行数据存储。

2 试验研究

在本节中，将混合整数二次规划（MICP）模型作为DN重新配置的有效工具应用于DN，以展示每小时重新配置的潜力，所提重构模型在通用代数建模系统中编程。该系统是一种高级建模语言，并使用混合整数优化求解器进行求解。选择MICP方法的原因是它可得到全局最优解并能准确地进行灵敏度分析。

值得一提的是，为了使MICP方法实现全局最优解，具有大组合搜索空间的大型网络可能需要大量的计算频次。但通过接受与全局最优解的微小距离，可减少计算时间。已有研究对该方法的性能进行了深入分析，并证明了其对大型DN的适用性。在本文中，与测试系统相关的信息用于研究结果。本文选择文献中广泛使用的33总线系统来分析日内重构的价值。33总线系统的初始配置包括风能和太阳能发电的位置和容量。本文考虑所有荷载点具有相同的24小时荷载分布且负载分为住宅和工业用电，采用2种方式对负荷变化进行建模。

2.1 敏感度分析

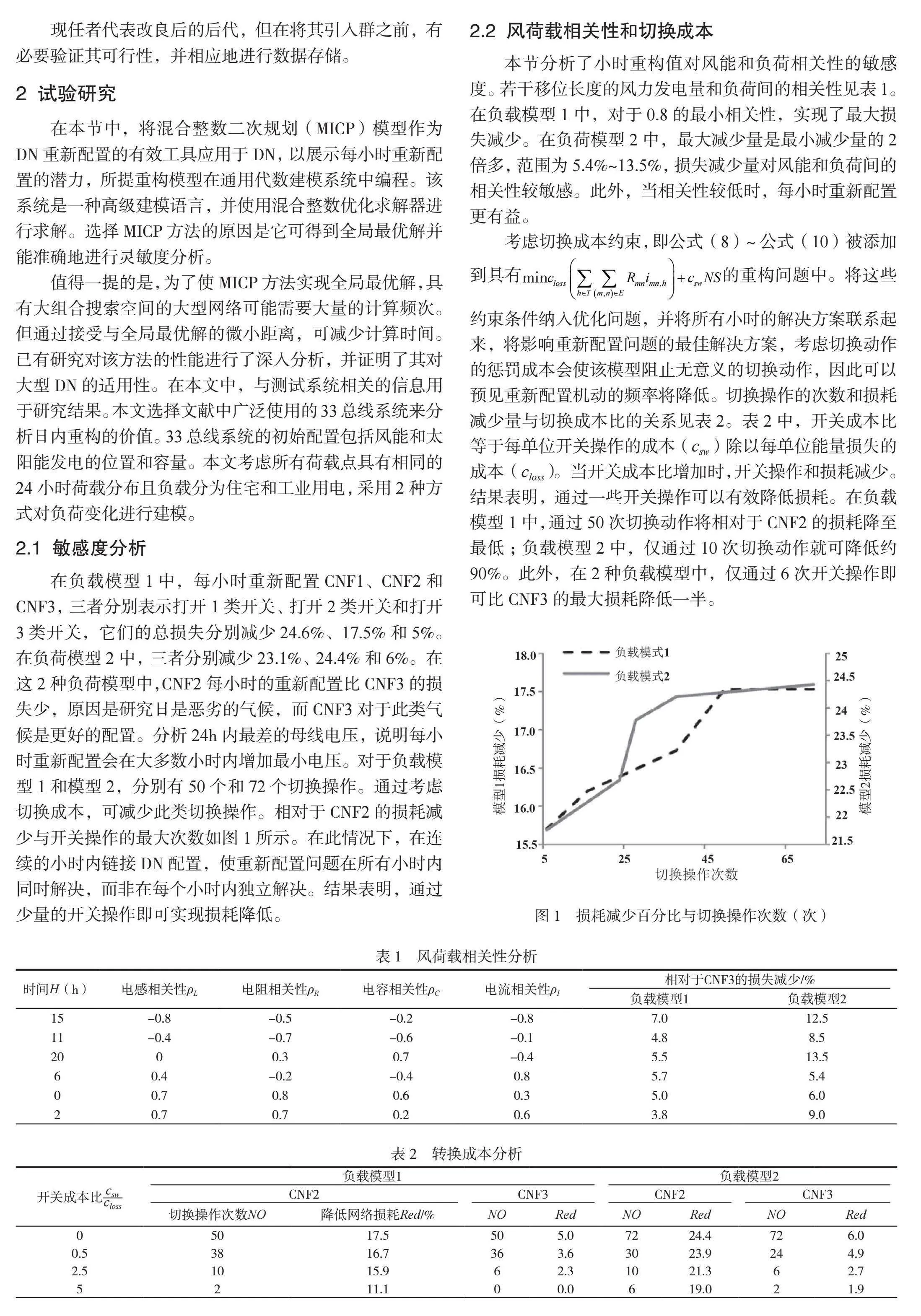
在负载模型1中，每小时重新配置CNF1、CNF2和CNF3，三者分别表示打开1类开关、打开2类开关和打开3类开关，它们的总损失分别减少24.6%、17.5%和5%。在负荷模型2中，三者分别减少23.1%、24.4%和6%。在这2种负荷模型中，CNF2每小时的重新配置比CNF3的损失少，原因是研究日是恶劣的气候，而CNF3对于此类气候是更好的配置。分析24h内最差的母线电压，说明每小时重新配置会在大多数小时内增加最小电压。对于负载模型1和模型2，分别有50个和72个切换操作。通过考虑切换成本，可减少此类切换操作。相对于CNF2的损耗减少与开关操作的最大次数如图1所示。在此情况下，在连续的小时内链接DN配置，使重新配置问题在所有小时内同时解决，而非在每个小时内独立解决。结果表明，通过少量的开关操作即可实现损耗降低。

2.2 风荷载相关性和切换成本

本节分析了小时重构值对风能和负荷相关性的敏感度。若干移位长度的风力发电量和负荷间的相关性见表1。在负载模型1中，对于0.8的最小相关性，实现了最大损失减少。在负荷模型2中，最大减少量是最小减少量的2倍多，范围为5.4%～13.5%，损失减少量对风能和负荷间的相关性较敏感。此外，当相关性较低时，每小时重新配置更有益。

考虑切换成本约束，即公式（8）～公式（10）被添加到具有的重构问题中。将这些约束条件纳入优化问题，并将所有小时的解决方案联系起来，将影响重新配置问题的最佳解决方案，考虑切换动作的惩罚成本会使该模型阻止无意义的切换动作，因此可以预见重新配置机动的频率将降低。切换操作的次数和损耗减少量与切换成本比的关系见表2。表2中，开关成本比等于每单位开关操作的成本（csw）除以每单位能量损失的成本（closs）。当开关成本比增加时，开关操作和损耗减少。结果表明，通过一些开关操作可以有效降低损耗。在负载模型1中，通过50次切换动作将相对于CNF2的损耗降至最低；负载模型2中，仅通过10次切换动作就可降低约90%。此外，在2种负载模型中，仅通过6次开关操作即可比CNF3的最大损耗降低一半。

3 结论

本文考虑了负载和风能、太阳能发电的变化，评估了配电网每小时重新配置的价值。对重构问题建立MICP模型，利用该模型可得到全局最优解，解决了在不限制切换操作的情况下每小时重新配置的问题，并将结果与固定配置进行了比较。结果表明，每小时重新配置可减少损失。本文还对风电与负荷相关性、切换成本和风电预测进行了敏感性分析。开关成本分析表明，通过少量的开关操作可大量降低损耗。本文的研究目的是为可再生能源条件下的配电网重构提供理论依据和实践经验，以促进电力系统的可持续发展和能源转型。希望本文研究能为解决可再生能源接入问题和电网运行的可靠性提供新的思路和方法，推动清洁能源的广泛应用。

参考文献

[1]廖秋萍，吕林，刘友波，等.考虑重构的含可再生能源配电网电压控制模型与算法[J].电力系统自动化，2017，41（18）：32-39.

[2]刘佳.适应不确定因素的输配电系统优化规划研究[D].上海：上海交通大学，2019.

[3]赵金利，李雨薇，李鹏，等.基于二阶锥规划的有源配电网SNOP电压无功时序控制方法[J].高电压技术，2016，42（7）：2134-2141.

[4]靳晓凌，赵建国.基于改进二进制粒子群优化算法的负荷均衡化配电网重构[J].电网技术，2005，23（29）：40-48.

[5]邓鹏.基于深度学习的配电网网损及重构研究[D].贵阳：贵州大学，2022.