基于改进多元宇宙算法的配送路径优化研究

摘 要：随着城镇化速度加快，城乡结合区域配送问题受到广泛关注。由于城乡间交通条件存在差距，因此配送车队构成和路径安排成为制约物流运输的主要矛盾。本文针对如何降低城乡混合区域条件下的配送成本，构建了模糊时间窗混合车队的城乡混合区域配送的车辆路径数学模型（The vehicle routing problem in mixed urban and rural and regional distribution of mixed fleet，VRP-MURMF）数学模型，并提出一种基于模拟退火算法改进的多元宇宙算法，采用逆序轮盘赌策略，使其在一定概率下向较差宇宙方向移动，避免陷入局部最优，在对比试验中，在探索后期比其他算法仍然具有较强的寻优能力，证明了本文算法的有效性。

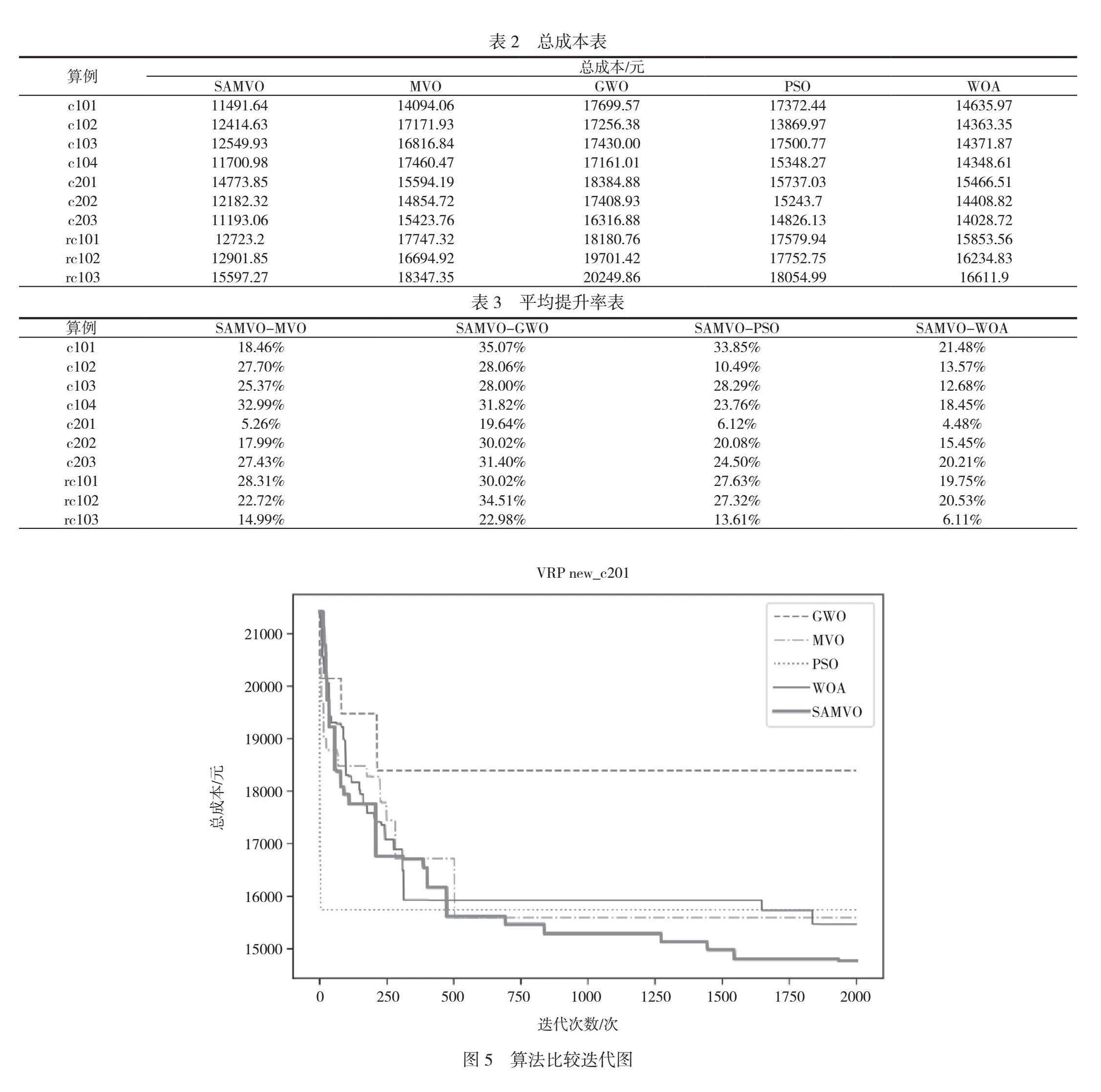
关键词：多元宇宙算法；配送成本；城乡混合区域；车辆路径优化

中图分类号：F 25" " " " " " 文献标志码：A

目前，我国城镇化率不断加快和乡村交通条件进一步提升，城市和乡村不同地区物流配送问题受到持续关注[1]。随着社会发展和技术创新，物流配送方式日益多样化。特别是在混合车队的路径优化中，不同类型的配送工具需要协同运作，使路径规划更复杂并具有挑战性[2-3]。因此本文研究了在模糊时间窗下混合车队的城乡混合区域配送的车辆路径优化问题（VRP-MURMF）。对于配送区域包括城市和乡村2类区域且由一个配送中心的2类配送工具（油车、电车）配送的情况，提出了基于模拟退火的多元宇宙算法，提高了算法跳出局部最优的能力和勘探能力。

1 问题描述与模型构建

1.1 问题描述

本文研究的混合车队城乡混合区域配送问题可以描述为在软时间窗约束条件下，单一配送中心由混合车队对城、乡2类区域进行配送，具体包括以下7个假设。1）一个配送中心。2）每个配送节点只被一辆车服务。3）配送中心有2种车型，即油车和电车。4）载重不允许超过最大载质量，客户位于城市和乡村。5）车辆在乡村和城市能耗速度不同。6）车辆的电量和燃油量充足，每个车型的最大载质量已知。7）每条配送线路的客户总需求量小于等于车辆最大载质量，配送车辆从配送中心出发，最终返回配送中心。

1.2 数学模型

VRP-MURMF针对配送的总成本Fmin构建函数。总成本Fmin包括C1（固定成本）、C2（行驶成本）、C3（能耗成本）、C4（碳排放成本）和C5（惩罚成本）。综上所述，VRP-MURMF的具体数学模型如公式（1）所示。

Fmin=C1+C2+C3+C4+C5 （1）

1.2.1 固定成本

单次配送的固定成本不会随距离等因素变化而变化，通常是配送的汽车数量和单位固定成本的乘积。

（2）

式中：i、j为配送节点；{1，...，N}为客户集合；AKE为电车固定成本；AKC为燃油汽车固定成本；xij为{0，1}决策变量，油车或电车从节点i配送至节点j时xij=1，否则为0。

1.2.2 行驶成本

配送过程中车辆的行驶成本会因行驶里程的变化而变化，如公式（3）所示。

（3）

式中：BKE为电车单位距离成本；BKC燃油汽车单位距离成本；dij为节点i、j间的距离。

1.2.3 能耗成本

在配送过程中，车辆由燃油或电能消耗产生的成本会因车辆行驶距离变化而变化，同时城乡间的道路条件不同，当2个配送节点都是乡村节点时，其单位成本也会不同，公式（4）所示。

（4）

式中：DKE为电车单位距离能耗；DKC为燃油汽车单位距离能耗；gKE为电车单位能耗成本；gKC燃油汽车单位能耗成本；p为农村能耗差异系数。

1.2.4 碳税成本

碳税是一种促进节能减排的重要手段。碳排放成本=碳排放量×单位碳税系数α[4]。乡村区域交通设施不完善，与城市相比，路况有一定不足，因此乡村的碳排放量更高，如公式（5）所示。

（5）

1.2.5 惩罚成本

在配送过程中，客户满意度和配送到达时间的隶属关系函数式如公式（6）所示。

（6）

根据客户满意度可以计算出配送过程中产生的惩罚成本，如公式（7）所示。

（7）

式中：客户最大满意度以时间窗[ETi，LTi]长度的一半为标准，设定客户可接受最早时间为EETi=ETi-（LTi-ETi）/2，可接受最晚时间为 ELTi=LTi-（LTi-ETi）/2；Si为车辆到达节点i的时间；μ（Si）为节点i的客户满意度；n为配送客户数量；Q为单位满意度惩罚成本。

2 基于模拟退火的改进多元宇宙算法

标准的多元宇宙算法针对的是连续性问题，而车辆路径优化问题是典型的离散问题，因此需要对算法进行离散化处理[5]。由于搜索策略以相对最优宇宙作为搜索区域，因此在迭代后期，种群越来越趋于同质化，所选出的最优宇宙趋于相似，搜索效率降低，不易跳出局部最优。针对以上问题，本文提出了基于模拟退火的改进多元宇宙算法（multi-verse optimizer variation，SAMVO）。

2.1 参数设定

SAMVO算法迭代采用轮盘赌机制，对排序后的宇宙膨胀率进行选取，并通过黑洞和白洞进行宇宙间的物质交换，如公式（8）所示。

（8）

式中：r1、r2和r3分别为[0，1]间的随机数，用于后续的随机操作；xkj为通过轮盘赌策略选择出来的第k个宇宙的第j个分量；NI（Ui）为第i个宇宙的归一化膨胀率。

设定WEP（Wormhole Existence Probability）为虫洞存在可能性系数，定义了宇宙空间内虫洞存在的可能。TDR（Travelling Distance Rate）代表物体在最优宇宙附近虫洞转换的距离。二者分别如公式（9）、公式（10）所示。

（9）

（10）

式中：WEPmin与WEPmax分别为0.2与1；l为当前迭代次数；L为最大迭代次数；p为随迭代次数改变的探测速度，该值越高，算法在局部区域探测速度越快，为了开发准确性，设定p=6。

2.2 编码与解码

进行编码时，每个宇宙的编码代表一条配送路径的方案。假设有1个配送中心，kc辆燃油汽车，ke辆电车，v个充电桩，m个城市客户，n个农村客户，各客户节点和配送车辆采用自然数进行编号且编号固定，离散且唯一。进行编码时，先对车辆节点进行随机排序，再将客户节点和充电桩节点随机插入，形成初始随机编码。例如当kc与ke分别为2，l为1，m与n分别为4时，形成的编码如图1所示。

2.3 黑白洞转移

采用随机原子操作（交换、插入和转移操作）[6]，具体操作如下。如果r1≤NI（Ui），就通过轮盘赌策略所选出的较优宇宙Uk进行转移，比较每个Uk和Ui，将第一个不同分量作为操作的起始分量Uia，在该分量后随机选择一个分量Uib，对这2个分量进行随机操作，生成U'i。比较Ui和U'i的适应度膨胀率NI（Ui）与NI（U'i），选取较大者更新为新的Ui。

2.4 关于向最优宇宙进行探索

在最优解的邻域进行开发，结合上述编码方式制定最优宇宙邻域搜索机制。在最优宇宙中随机选择一个车辆节点，对该车辆节点下的2个客户节点进行随机原子操作，生成新的解。如果更新后解的膨胀率比原解的膨胀率大，就将其替换为新的Ui。以插入操作为例，操作过程如图2所示。

2.5 关于向较差宇宙进行移动

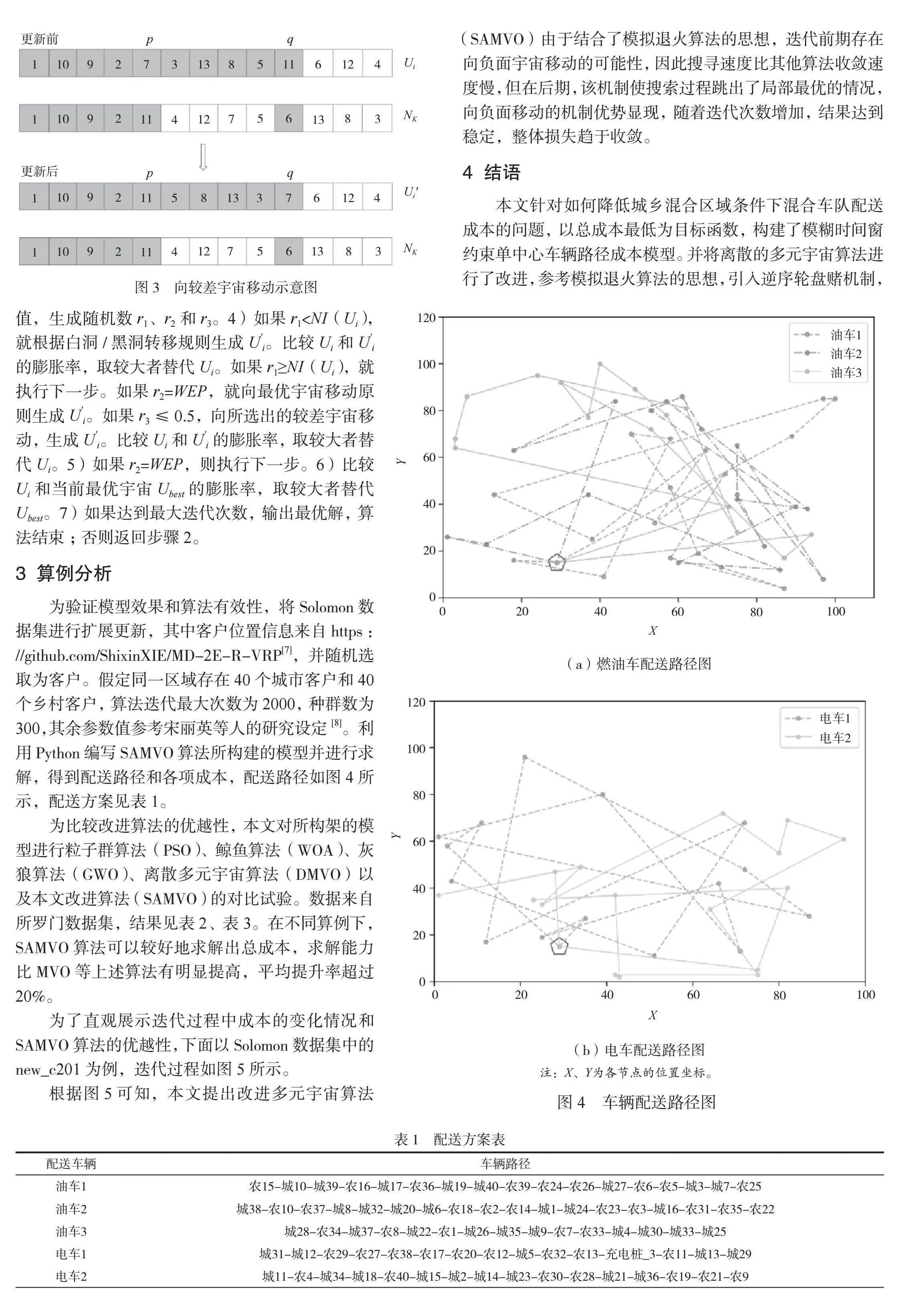
为避免在探索后期陷入局部最优，在搜索机制上结合模拟退火算法的思想和在一定概率下向负面解进行探索，增加了算法的灵活性。如果随机数r3≤0.5，就向通过逆序轮盘赌策略所选出的较差宇宙NK进行移动。比较每个MK和Ui，将第一个不同分量作为操作的起始分量Uip，在该分量后随机选择一个分量Uiq，对这2个分量进行随机的原子操作，生成U'i。比较Ui和U'i的适应度膨胀率NI（U），选取较大者作为新的Ui。以反转操作为例，如图3所示。

2.6 整体算法步骤

整体算法步骤如下所示。1）初始化种群、WEPmin、WEPmax以及最大迭代次数等相关参数。2）计算每个小宇宙的NI（U），用轮盘赌机制（逆轮盘赌机制）选择较优的宇宙个体UK和较差的宇宙NK。3）通过每个个体Ui计算WEP和TDR值，生成随机数r1、r2和r3。4）如果r1lt;NI（Ui），就根据白洞/黑洞转移规则生成U'i。比较Ui和U'i的膨胀率，取较大者替代Ui。如果r1≥NI（Ui），就执行下一步。如果r2=WEP，就向最优宇宙移动原则生成U'i。如果r3≤0.5，向所选出的较差宇宙移动，生成U'i。比较Ui和U'i的膨胀率，取较大者替代Ui。5）如果r2=WEP，则执行下一步。6）比较Ui和当前最优宇宙Ubest的膨胀率，取较大者替代Ubest。7）如果达到最大迭代次数，输出最优解，算法结束；否则返回步骤2。

3 算例分析

为验证模型效果和算法有效性，将Solomon数据集进行扩展更新，其中客户位置信息来自https：//github.com/ShixinXIE/MD-2E-R-VRP[7]，并随机选取为客户。假定同一区域存在40个城市客户和40个乡村客户，算法迭代最大次数为2000，种群数为300，其余参数值参考宋丽英等人的研究设定[8]。利用Python编写SAMVO算法所构建的模型并进行求解，得到配送路径和各项成本，配送路径如图4所示，配送方案见表1。

为比较改进算法的优越性，本文对所构架的模型进行粒子群算法（PSO）、鲸鱼算法（WOA）、灰狼算法（GWO）、离散多元宇宙算法（DMVO）以及本文改进算法（SAMVO）的对比试验。数据来自所罗门数据集，结果见表2、表3。在不同算例下，SAMVO算法可以较好地求解出总成本，求解能力比MVO等上述算法有明显提高，平均提升率超过20%。

为了直观展示迭代过程中成本的变化情况和SAMVO算法的优越性，下面以Solomon数据集中的new_c201为例，迭代过程如图5所示。

根据图5可知，本文提出改进多元宇宙算法（SAMVO）由于结合了模拟退火算法的思想，迭代前期存在向负面宇宙移动的可能性，因此搜寻速度比其他算法收敛速度慢，但在后期，该机制使搜索过程跳出了局部最优的情况，向负面移动的机制优势显现，随着迭代次数增加，结果达到稳定，整体损失趋于收敛。

4 结语

本文针对如何降低城乡混合区域条件下混合车队配送成本的问题，以总成本最低为目标函数，构建了模糊时间窗约束单中心车辆路径成本模型。并将离散的多元宇宙算法进行了改进，参考模拟退火算法的思想，引入逆序轮盘赌机制，减少陷入局部最优的情况。通过本文改进的多元宇宙算法来求解Solomon数据集和扩展数据集中部分算例，证明了本文算法解决该情况下车辆路径问题的有效性和优越性。

参考文献

[1]李英，张鹏威，吴一帆.电动汽车/传统汽车混合车队车辆配置及路径优化模型[J].系统管理学报，2020，29（3）：522-531.

[2]LI Y，ZHANG P W，WU Y F.Vehicle routing problem with mixed fleet of conventional and electric vehicle[J].Journal of systems amp; management，2020，29（3）：522-531.

[3]ISLAM M A，GAJPAL Y，ELMEKKAWY T Y.Mixed fleet based"green clustered logistics problem under carbonemission cap[J].Sustainable"cities and society，2021，72：103074.

[4]许菱，杨林超，朱文兴，等.农村电商物流下无人机与车辆协同配送路径优化研究[J].计算机工程与应用，2024，60（1）：310-318.

[5]唐慧玲，唐恒书，朱兴亮.基于改进蚁群算法的低碳车辆路径问题研究[J].中国管理科学，2021，29（7）：118-127.

[6]方恒，朱建鸿.基于离散多元宇宙算法的柔性作业车间调度[J].组合机床与自动化加工技术，2023（10）：174-178.

[7]张强，姜慧清，王颖等.基于离散多元宇宙算法求解车辆路径问题[J].电子科技大学学报，2021，50（6）：890-898.

[8]谢世鑫，王旭，杜建辉，等.考虑同城配送的多产品多中心两级物流网络设计及车辆路径研究[J].管理工程学报，2023，37（3）：178-190.