“基于思想方法”视角下的高中数学教学探究

数学思想方法是数学学习的核心价值，是数学知识体系架构的灵魂，它如同引领学生深入数学学习的钥匙，能够帮助学生打开理解数学概念、公式、定理等基础知识的大门，既能强化学生对概念、公式、定理等数学基础知识的理解，又能锻炼学生的逻辑和抽象思维，为学生更高纬度的数学学习打下基础。数学思想方法蕴含在数学知识的传授中，具有潜移默化影响的特点，所以教师在规划课堂教学活动时，要深入钻研教材，善于通过对教材和课标的研究，总结归纳出知识中蕴含的基本思想方法，在此基础上，精心地设计教学过程，在知识讲授的同时渗透思想方法，提升学生的数学素养。

1.基本思想方法

数学基本思想源自史宁中撰写的《数学思想方法概论》，先后通过义务教育和高中课程标准呈现。史宁中第一次明确了数学基本思想的判断标准，这些思想首先是数学产生和发展所必须依赖的，其次是通过对数学的学习应该具备的基本思维方式。数学方法是数学思想在实践中的直接体现，它将抽象的数学思想转化为具体、可操作的步骤和程序。数学思想蕴含在数学知识学习中，是指向数学思维活动内部的，是本质性的；数学方法体现在数学解题过程中，是外显的、具体的，指向数学思维活动的外部，具有可操作性。数学基本思想的核心要素（如抽象、推理、模型等）蕴含在数学思想方法中，是抽象、概括更高层次的数学思想方法而形成的更深刻的观点。

数学思想方法是以数学知识和技能为基础，以数学思想为内涵，以数学方法为外延，紧密联系数学教育教学和数学学习过程，指向数学活动经验的积累和思维习惯的形成，二者的交融和统一即数学思想方法。

2.“基本思想方法”视角下的高中数学教学实施

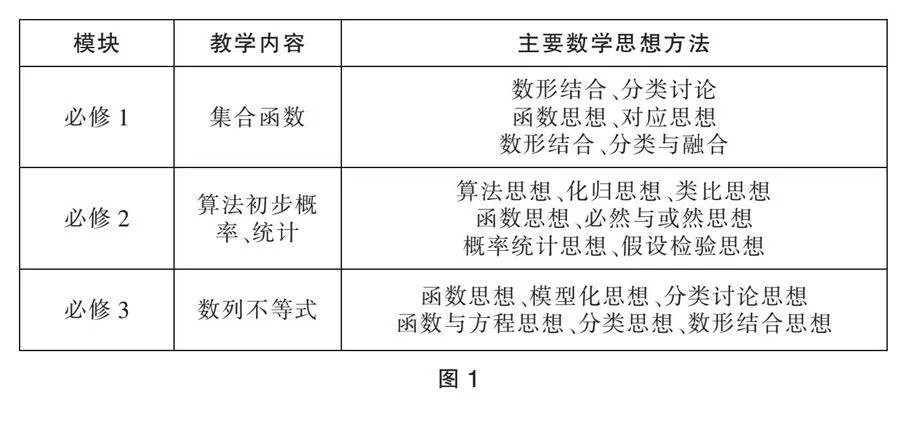
数学思想方法与知识内容相辅相成，共同构成了数学课程的核心，在高中数学教学中要将知识教学与思想方法的培养紧密结合，形成一个有机整体。在新的背景下，教师要深入研究新教材、新课标，做到对教材每个知识点都有深入的理解和把握，同时深入探究知识点中蕴含的思想方法，课堂教学中，在对知识讲解的同时，更注重对学生思维的培养和启迪，让知识的传授过程和思想方法的领悟过程有机融合。比如必修1集合和函数、必修3算法初步和概率统计、必修5数列和不等式，我们可以梳理和归纳如图1。

挖掘高中数学知识中的思想方法是教学中渗透思想方法的前提，只有充分地研究教材、研究课标，才能析出高中数学知识中的思想方法，合理设计教学，在知识的传授中渗透数学基本思想方法，潜移默化地影响学生，下面以不等式知识为例，探究分析不等式中的数学思想方法。

人教版新教材不等式放在了高一必修1第二章，不等式安排在高一年级，衔接起初高中知识，起着承上又启下的作用。不等式知识中包含着高中数学中很多重要的思想方法，例如数形结合、函数与方程、分类讨论、化归等。教师在不等式教学中应注重基础知识与思想方法的有机结合，通过个性化教学、深度挖掘、归纳总结和实践应用等策略，让不等式的知识架构丰盈起来，让知识和思想同步领悟，为学生的数学素养和思维能力的提升奠定坚实的基础。

2.1数形结合思想

数与形作为探究同一数学问题的双重视角，非但不相斥，反而相辅相成，构成了彼此转化的桥梁与通道。在解决数学难题时，数形结合的思想方法尤为关键，它主要分为两大策略：“以形助数”与“数转形现”。

“以形助数”就是利用图形的直观性来理解和解决数学问题，这一过程要求我们将图形的特性、属性转化为代数语言，换而言之就是我们利用代数式、方程或不等式等代数形式表达图形的特征，方便我们依据数学定理、公式进行逻辑推理与求解，使得复杂的数量问题形象化、可视化，而“数转形现”则是一种逆向的思考，它将原本抽象、不太容易直接理解的代数问题，转化为比较直观形象的几何图形问题。数形结合的思想方法串联起了数学中的几何和代数，搭建起了数与形之间的桥梁，数形结合思想是数学中数形和谐统一的完美体现，更是一种高效的解题工具与策略。不等式中有着很多数形结合思想的应用，在日常的课堂教学中，利用不等式的知识渗透数形结合思想方法，在加深学生对知识的理解的同时，也让学生受到了数学之美的熏陶。

（一）基本不等式

在基本不等式章节学习中，利用了数形结合的几何方法理解基本不等式。

如图2，AB是圆的直径，点C是 AB上一点， AC=a，BC=b。过点C作垂直于AB的弦DE，连接 AD，BD。你能利用这个图形得出不等式 ≤的几何解释吗？

如图：

设半径为R，则直径 AB=a+b， R=。

由垂径定理可知CD= 。

由图2可知，CD≤R，

故≤

显然，当且仅当点C与圆心重合，即a=b时，等号成立。

（二）一元二次不等式及其解法

求不等式x2－5x+4≥0的解集。

解：作函数 y=x2－5x+4的图象，如图3，函数y=x2－5x+4与x轴的交点横坐标为x1=1，x2=4。求解一不等式x2－5x+4≥0，即是求满足函数 y=x2－5x+4图像在x轴上或者在x轴上方的所有x的集合，所以原不等式x2－5x+4≥0的解集为x｜x≤1或x≥4。

在不等式知识中，体现了数形结合思想的精妙之处的题型有很多，这些不等式问题如果只是单纯从代数角度思考，是比较繁琐的，比如确定数值范围问题，如果将代数问题转化为几何问题，就能形象直观地分析问题，也可以有效地降低运算量，提升解题效率。数形结合的应用促进了图形与代数知识间的深度融合，加深了学生对数学内在逻辑与结构的理解。

2.2函数与方程思想

函数思想是一种洞察数学对象间动态量变关系，从运动与变化的维度出发，依据给定条件构建或确立函数关系式。函数思想核心在于运用函数的定义、性质以及变换规律，把数学问题转化为函数问题；方程思想则侧重于在动态变化分析问题中的变量变化特征，利用未知数间的等量关系构造方程，方程思想的本质是数学知识中的变与不变。

函数思想与方程思想在高中数学教学中互为补充，相辅相成。函数与方程两种思想的紧密结合，为学生灵活地应对各种数学问题提供了强大的解题工具。在高中数学课堂教学中进行函数与方程思想的渗透，可以帮助学生很好地理解和掌握数学概念和性质，实现数学素养的全面提升，不等式中函数与方程思想应用十分广泛。

如：构造函数求参数取值。

例：已知函数f（x）=1+2x+k·4x，其中k为常数，若当x∈（－∞，2］时，有f（x）>0，求k的取值范围。

分析：含参不等式问题是高中数学的难点，面对这一类问题，我们经常分离参数k，然后构造新的函数，含参问题就可以转化为不含参数的函数问题，进而利用函数的有关知识去解决。

解：当x∈（－∞，2］时，有f（x） > 0成立，即1+2x+k·4x> 0成立，

分离参数后构造新的函数，是含参不等式常用的解题方法，分离参数后求解的问题就转化为了无参数的函数问题，就可以利用函数的有关性质来求解。不等式中涉及多个变量和条件时，我们往往利用方程来建立变量之间的等量关系，将问题中的未知量转化为已知量，从而让复杂的多变量问题变简单。

函数与方程思想对学生深入理解数学的本质和规律有着很大的帮助。因此在高中数学教学中，教师应该注重课堂教学设计，在教学实施过程中培养学生的函数与方程思想意识以及灵活运用这些思想解决问题的能力。

2.3分类讨论思想

分类讨论思想是一种深刻而灵活的数学策略，数学中有很多错综复杂的难题，这类问题要使用一种系统化、条理化的方法，才能够思路清晰地解决问题。分类讨论思想的核心是根据问题本身的特性或内在规律，选取合适的分类标准，然后按照分类的标准将复杂问题拆解为几个相对简单、方便处理的问题，最后归纳各部分的结论，总结出原问题全面的结果。

不等式中分类讨论思想也随处可见，例如在求解分式不等式时，会采用化归的思想，把分式不等式转化为整式不等式，而整式不等式的解决，又要运用分类讨论的思想，按照分母的正负性进行分类讨论；比如在处理含参不等式时，要根据参数的不同取值范围进行分类讨论，分类讨论思想在不等式解题中有着独特的魅力。

如含参比较大小问题。

比较（a+1）2与a2－2a+3的大小关系。

分析：作差比较大小，

分类讨论思想在不等式知识中的应用是一种重要的解题方法，当学生在面对复杂的不等式问题时，通过不等式的性质、结构或条件的不同，把问题分解为几个相对简单问题，然后分别进行讨论解决，最后归纳总结问题的完整解。分类讨论时要做到以下几点：一是分类应逐级进行，避免越级跳跃，以确保讨论的条理性和逻辑性；二是在同一分类级别内，必须采用统一的分类标准，以保持分类的一致性；三是分类时要力求全面，不重不漏。

2.4化归思想

化归是转化和归因的简称，化归是“转化”与“归因”的紧密结合，转化是手段，归因则是目的。化归是把一个问题从难到易、从繁到简地转化出来，转化是高中数学处理问题的方法和途径，本质上就是寻求问题解题思路与方法，当问题比较难或者比较复杂时我们采取的策略。化归是实现新旧知识或问题动态转换的重要数学思想方法，也是有效的思想策略和方法，正确的转化是解题成功的关键。化归思想一般按照以下模式如图4。

如：求分式不等式解集问题。

求不等式≤0的解集

分析：对于分式不等式≤0，第一种思路是把分式不等式转化为已知的分式知识：同号为正，异号为负，分母不为零，即转化为f（x）≤0g（x）>0，或者f（x）≥0g（x）<0，另外一种思路是等价转化为f（x）g（x）≤0g（x）≠0，即将分式不等式通过转化等价于整式不等式，而整式不等式也是我们已知掌握的，化未知为已知，化旧知为新知，这就是化归思想的应用，化归思想求一元二次不等式解集，解决含参不等式问题等中也有体现。

3.总结

数学学习显性的是丰富的知识体系、精确的模型构建以及严谨的逻辑推理，隐性的是数学的基本思想，它们构成了数学学科的核心灵魂，对学生而言，数学基本思想方法，是他们深入理解数学知识，灵活运用数学知识解决问题的钥匙，也是培养他们核心素养、发展高阶思维能力的基石；教师是数学思想方法的传播者和启迪者，课堂教学直接影响着学生对数学思想方法的理解和掌握程度，因此教师在规划课堂教学活动时，要深入钻研教材，善于总结归纳知识中蕴含的基本思想方法；通过对教材和课标的研究，灵活设计课堂教学过程；在课堂教学的实施过程中，通过对教材和课标的研究，总结归纳出思想方法并巧妙地融入课堂教学中，使学生在领会高中数学知识的“体”时又领会了其“魂”，同时又对学生的数学思维能力起到了锻炼作用，提高学生的数学素养。

责任编辑 钱昭君