小学数学教材结构化研读路径

摘 要 帮助学生建立结构化数学知识体系的基础是教师能对教材进行结构化研读。因此，可以以整体联结为核心理念，把握“课时—单元—整体”路径，三维建构知识结构网络；遵循“主题—单元—课时”路径，三层聚焦知识进阶路径；立足“单元—课时—体系”路径，双向架构知识结构体系。

关 键 词 小学数学；教材结构化；知识结构网络；知识进阶路径；知识结构体系

引用格式 龚哲荣.小学数学教材结构化研读路径[J].教学与管理，2024（32）：67-71.

《义务教育数学课程标准（2022年版）》在课程实施的教学建议第二条中指出：“在教学中要重视对教学内容的整体分析，帮助学生建立能够体现数学学科本质的、对未来学习有支撑意义的结构化的数学知识体系。”[1]小学数学教材选用“知识循环、螺旋上升”的方式进行编排，将不同领域的知识内容分散处理，并以单元为“群”、课时为“点”进行教学。基于此，笔者以整体联结为核心理念，针对不同内容、不同需求、不同的切入点探寻三种深度研读教材路径，架构清晰、全面、完整的知识结构体系。

一、“课时—单元—整体”三维建构知识结构网络

知识结构网络的整体架构，不能只是基于单课时教学内容狭隘地“读”教材，而需要在解读课时内容的基础上，对课时内容进行深度剖析，结合要素之间的关联点明确课时结构。然后，依托单元中不同课时之间的联结点厘清单元架构，再从单元内容出发进行同质单元对比和相关单元的勾连，从而架构整体知识结构网络。

1.研读要点，寻找关联，明确课时内容结构“点”

教师应“全方位搜索”教材内容，仔细阅读每道例题、习题以及旁白、提示，在此基础上挖掘其背后所蕴含的内容要点和知识元素，然后厘清每个内容要点和知识元素之间的联系，结合教材分析学习方式和思维路径，明确课时内容结构。

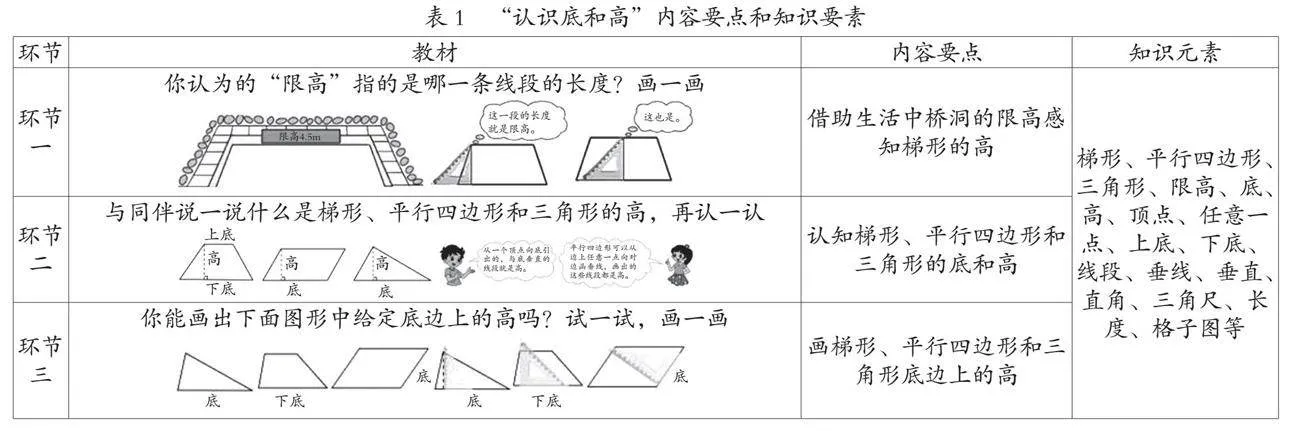
如北师大版《数学》五年级上册“认识底和高”一课，教材编排了3个教学环节和4道练习题，其蕴含的内容要点和知识要素见表1。

从表1中可以看出，本课首先借助生活经验，把桥洞的限高与梯形的高进行对接进而认知梯形的高，同时结合梯形、三角形、平行边形的一致性进行类比迁移，认识高，理解高的本质。在此基础上依托已学的三角尺画垂线，学会画底边上的高，并通过练习1和练习2进行巩固强化。练习3和练习4则借助格子图的创作活动，动态对比体会等底等高、等高不等底图形的多样性和可变性。

2.全面分析，厘清脉络，梳理单元贯通结构“线”

教师要全盘分析每一课时的教学内容和目标要求，把每一课时内容纳入单元整体，从单元视角整体分析各课时内容之间的联系，以及知识呈现路径和学习序列，进而梳理单元知识结构线。

如北师大版《数学》五年级上册“多边形面积”单元安排了6个内容，每一课时的教学内容和目标要求见表2。

从单元整体知识结构出发，6节课分为“铺垫—探索—提升”三个阶段：“比较图形面积”和“底和高”是第一阶段的两节铺垫课，分别指向活动经验积累和基础概念学习，为后续推导图形的面积做好准备；第二阶段是三节面积推导课，从知识迁移、问题探索、方法多元逐层深入推进；练习五是第三阶段的巩固应用。

3.前后联结，整体贯通，建构整体知识结构“面”

教师可以从单元内容出发，用联系的眼光进行整体联结，寻找相关知识内容在不同年段、不同单元的编排，深度挖掘知识之间的来龙去脉，厘清知识发展脉络和学习路径，精准架构整体知识结构网络。

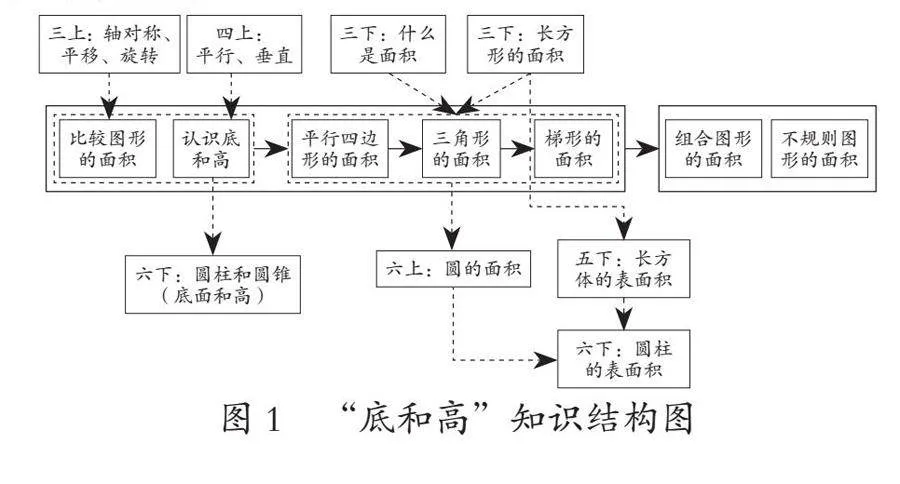
在学习“多边形面积”之前，学生在三年级已经学习了“什么是面积”和“长方形（正方形）的面积”，本册教材还将继续学习“组合图形的面积”和“不规则图形的面积”，到六年级将进一步学习“圆的面积”，此外在研究立体图形的侧面积和表面积时也有所运用。“底和高”的知识储备是四年级点到直线的距离和平行线之间的距离，在后续学习圆柱和圆锥时还会研究底面和高。基于以上分析，就可以形成如图1所示的知识结构图。

二、“主题—单元—课时”三层聚焦知识进阶路径

知识结构进阶路径的分析，要在通盘研读12册教材，了解知识内容编排的基础上，进行逐层解读、分段聚焦。在确立领域和主题的基础上，进行板块分析，了解单元整体进阶体系。针对每个单元进行课时解析、沟通对比，梳理课时内容推进序列。聚焦课时内容，进行深度剖析，联结环节逻辑，明确知识内容学习路径。

1.锚定主题，单元联通，了解单元编排体系

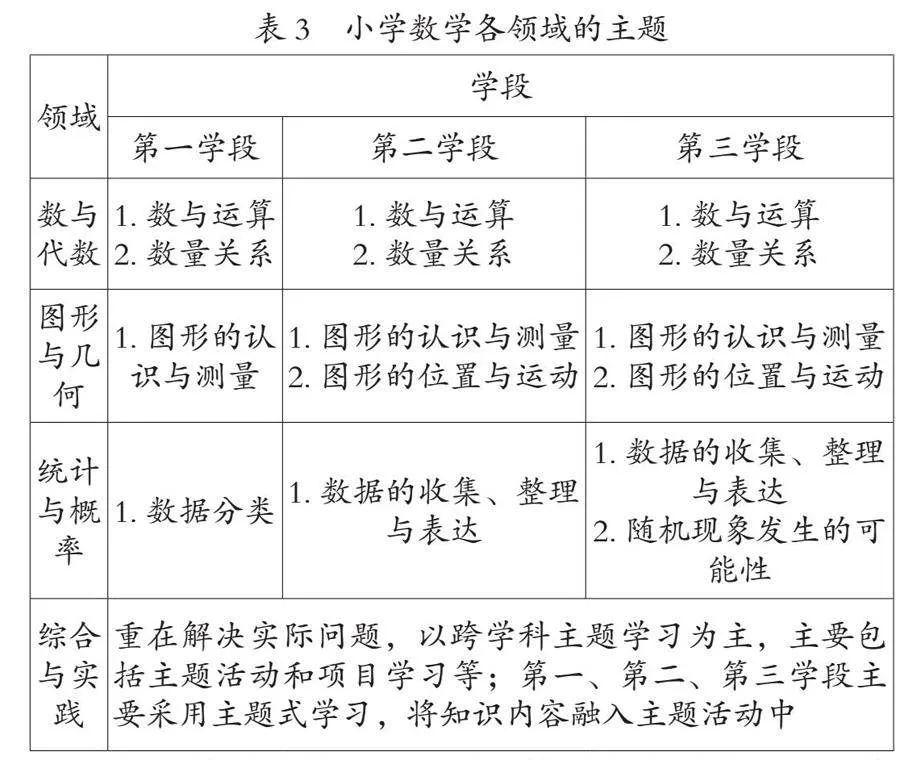
根据《义务教育数学课程标准（2022年版）》要求，数学课程内容由数与代数，图形与几何、统计与概率、综合与实践四个领域组成，每个学段的主题有所不同，具体内容见表3[2]。

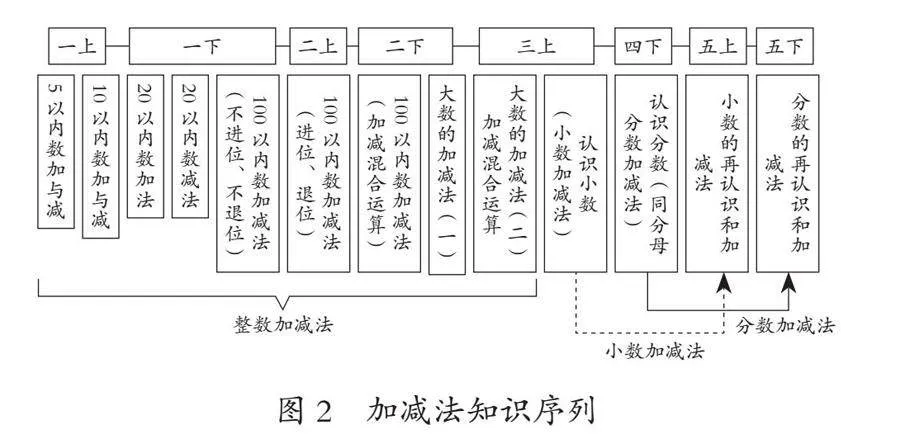
梳理单元编排顺序，厘清单元内容阶段序列，针对每个主题可分解为几个不同的板块内容。如“数与运算”包括“数的认识”和“数的运算”两个板块。其中数的运算包括整数、小数、分数的运算，涉及加减法、乘法、除法等不同运算。以加减法为例，北师大版《数学》用13个单元，以数的扩充为基线，以运算方法提升为坡度，按“5以内的数→10以内的数→20以内的数→100以内的数→大数→小数→分数”序列逐层深入如图2所示。

2.立足单元，课时联动，厘清课时编排路径

以单元编排体系为载体，全盘解析所有单元每个课时的教学内容，并依据课时内容同质联动，从而厘清整个板块课时联结路径。

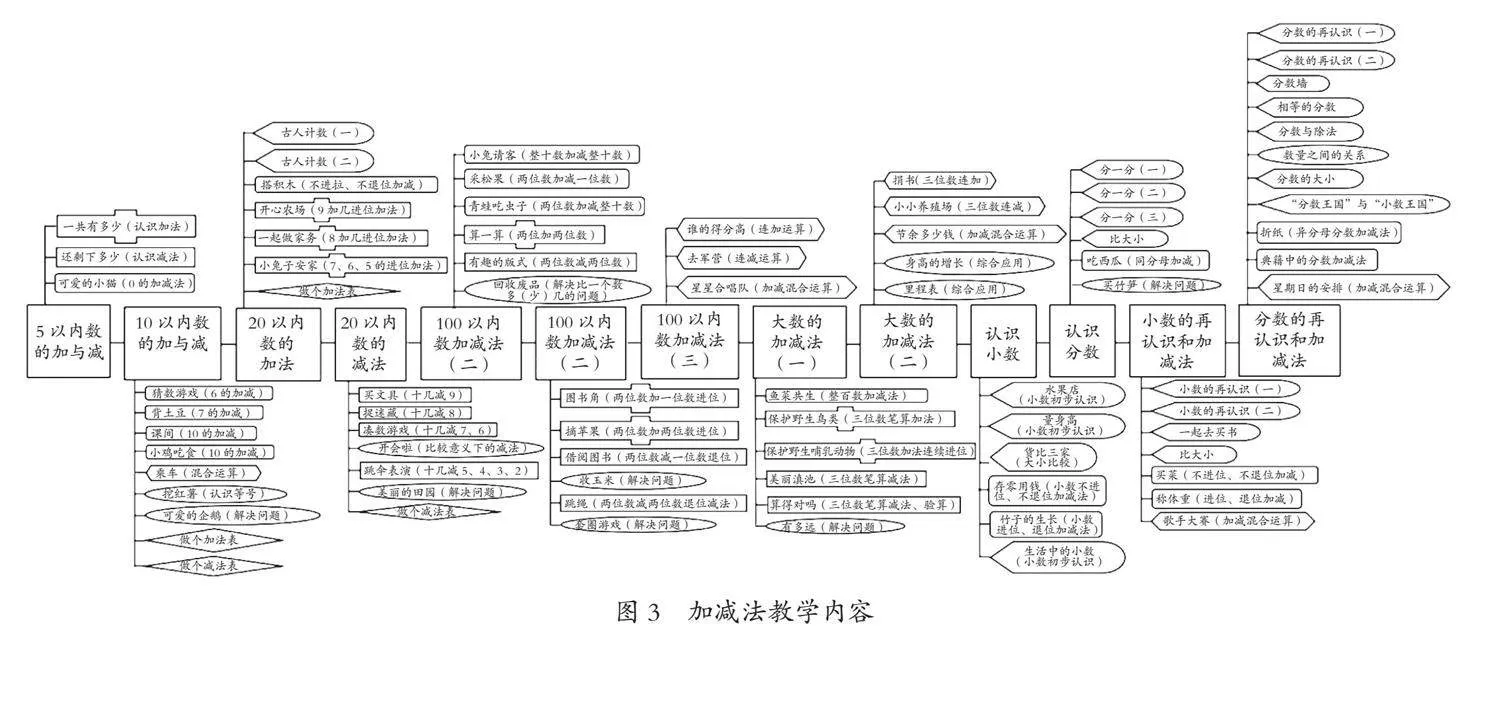
以加减法的13个单元为基础，教材共安排了82个内容（如图3所示），有21个内容涉及到数的认识板块。在余下的61个内容中：解决问题专项有11个内容，在保持数级扩充的同时，按部总关系、相差关系、综合应用逐层深入；混合运算专项有9个内容，在每个数级阶段都有编排；加减运算按原理路径从“相同计数单位相加减（整十、整百、同分母分数相加减）”延伸到“计数单位不同要转化（数位对齐、通分）”进行编排，在计算方法上则从“不进位、不退位”到“进位、退位”依次编排。

3.聚焦课时，内容联结，明晰知识学习路径

针对课时知识内容，教师要遵循“单元—课时”编排路径，找到前后相关联的课时，进行每个教学环节要点的对比分析，找准知识的联结点，进而明晰知识学习路径。

以北师大版《数学》三年级上册“认识小数”单元“存零用钱（不进位、不退位加减法）”一课为例。与其相关联的内容分别是二年级下册“大数的加减法（一）”单元和五年级上册“小数的再认识和加减法”单元。针对教材设计的探究加法算理、探究减法算理、总结算法三个环节，找到相对应的环节内容进行对比整理（见表4）。

对比整数加法和小数加法的探究过程，选用的材料与数的认识过程基本保持一致，沿着小棒、数线、计数器、元角分、小方块逐层深入。在三年级探究小数加法的第二种方法，借助元角分把小数转化成整数进行计算，沟通整数加减法与小数加减法之间的一致性。

对比算法总结的过程，学生经历“具体的数位对齐→相同数位对齐→用元角分说明小数点对齐→小数点对齐”逐层进阶的过程，从而打通整数加减法和小数加减法的算法一致性，即相同计数单位上的数相加减。

三、“单元—课时—体系”双向架构知识结构体系

单元是连接课时内容和知识体系的纽带，以单元为核心进行课时联结和板块延伸，可以快速有效地架构知识结构体系。教师应从单元整体视角出发，分析每一课时的知识内容，找准知识间的内在联系，架构单元内部结构。以单元为起点，进行知识的前后拓展、左右互通、上下联结，架构知识结构体系。

1.聚焦单元，联结课时，明晰单元内部结构

教师要站在单元视角整体分析课时内容，明确单元内容的组织序列，挖掘每个课时所蕴含的知识内容，分析它们之间的相互关联和内在逻辑，进而明晰单元知识结构。

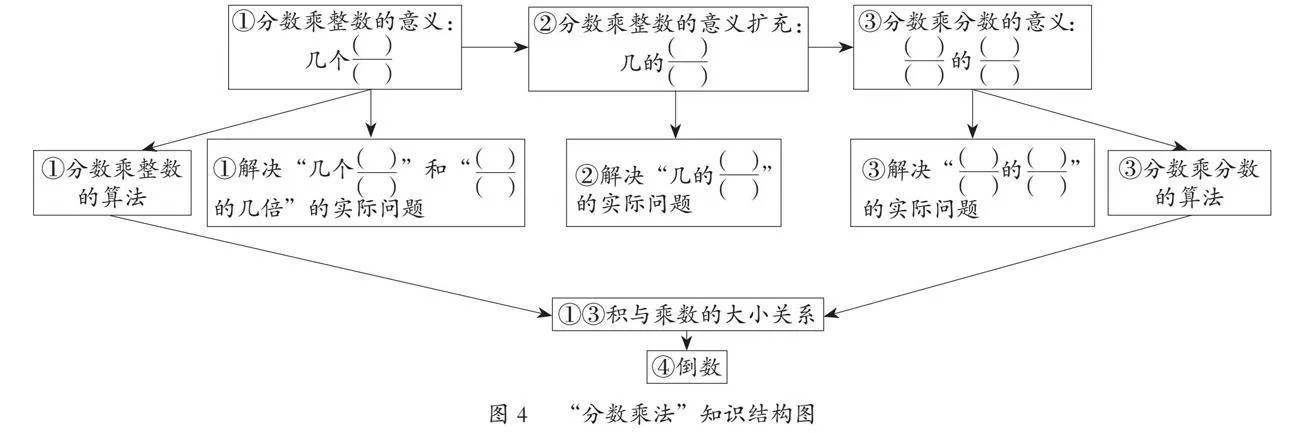
如北师大版《数学》五年级下册“分数乘法”单元，教材一共编排了分数乘整数、分数乘整数解决问题、分数乘分数、倒数四个教学内容，包含意义理解、算法总结、规律探索、实践应用等知识。根据他们之间的相互关联，本单元知识结构如图4所示。从“几个”“几的”“的”三个层次理解分数乘法的意义并解决实际问题，并在分数乘整数与分数乘分数算法归整和乘数与积的大小关系的基础上认识倒数。

2.立足单元，纵横贯通，厘清知识结构体系

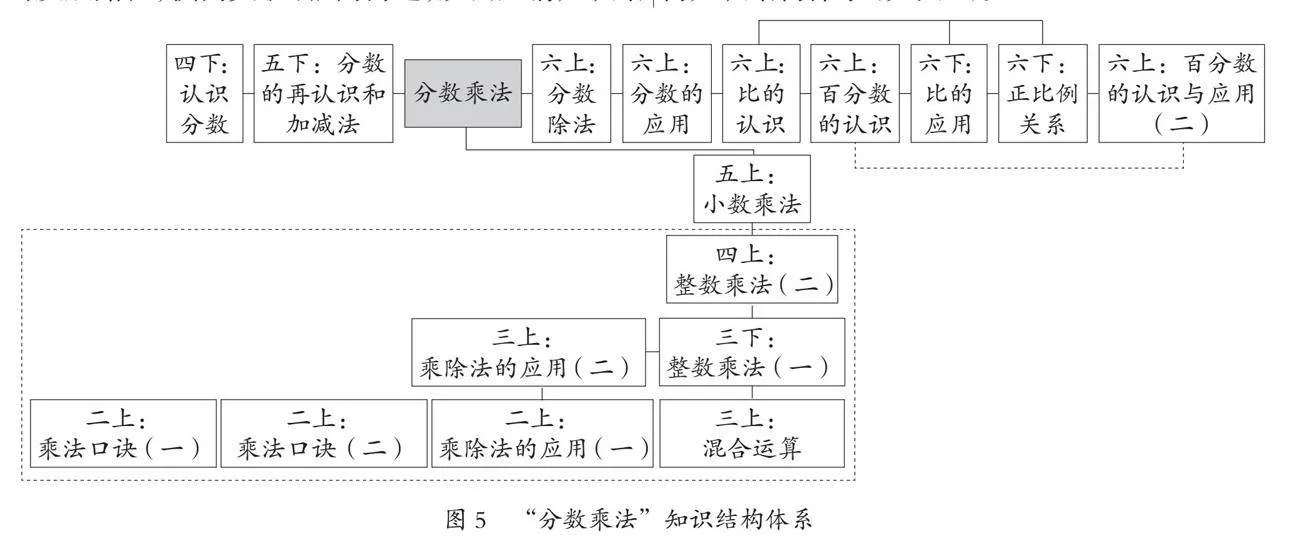
在单元内部结构分析的基础上，将单元内容置于整个小学阶段的数学知识板块之中，沿着单元知识元素的发展路径，横向关联、纵向沟通，从而厘清知识结构体系。如北师大版《数学》五年级下册“分数乘法”单元，可从分数路径横向关联和乘法路径纵向沟通两个维度拓宽延展，找准进阶层次和联结路线，从而架构知识结构体系（如图5）。

北师大版《数学》与分数相关的学习内容共编排了10个单元，在“分数乘法”之前教材分两个阶段学习分数、大小比较和加减法运算，后续则编排了分数除法、分数的应用、百分数的认识与应用、比和比例等相关内容。乘法运算则在乘法意义和乘法口诀的基础上，经历两、三位数乘一位数，两、三位数乘两位数，小数乘法，分数乘法四层进阶，完成整数、小数、分数三个不同阶段的乘法学习。

用联系的眼光整体研读教材是开展结构化教学的基础[3]。教师可以灵活选择研读教材的突破口，做到以小见大、以点带面、以联构体，关注知识的关联性、进阶性、整体性和一致性，有效贯通课时内容、超越单元视角、突破主题界限，建构连贯、交叉、立体的数学知识结构体系，助推结构化教学的深入实施[4]。

参考文献

[1][2] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022：85，16.

[3] 王哲燕，段安阳.小学数学“结构化”单元整体教学的理解与实践[J].教育科学论坛，2022（05）：22-25.

[4] 金怡婷.结构化提问：变“碎片”为“整体”[J].教育视界，2024（07）：25-28.

[责任编辑：陈国庆]