基于SFR模型的电网广义惯性分区评估方法研究

摘" 要： 近年来新型电力系统的电力电子化趋势愈发明显，一方面随着能源结构的调整，大量采用电力电子接口的新能源发电接入电网；另一方面随着节能技术的发展，负荷设备也逐步实现了电力电子化.由于电网中的电力电子设备占例不断提高，削弱了原有同步发电机、异步电动机的占比，给电网的安全稳定运行造成了不利影响.基于SFR模型提出了一种电力系统广义惯性的分区模型及其评估方法，并可用于分区补偿前后的性能对比.首先，面向电力电子化趋势建立了电网的SFR广义惯性分区模型；其次，根据仿真算例分别模拟惯性补偿前后的系统分区频率曲线，通过粒子群优化算法拟合惯性时间常数H，并计算相应的惯性分布均匀指数Dδ；再次，通过综合评估H和Dδ，分析惯性大小的改善及惯性分布均匀性；最后，基于评估结果进一步调整补偿措施，返回上述参数计算步骤直至满足设计评估要求.通过仿真算例验证了相关模型及相应评估方法的正确性与适用性.

关键词： 新型电力系统；电力电子化；惯性分区；广义惯性；评估方法

中图分类号：TM74""" 文献标志码：A""""" 文章编号：1673-4807（2024）05-063-07

DOI：10.20061/j.issn.1673-4807.2024.05.010

收稿日期： 2023-10-25""" 修回日期： 2021-04-29

基金项目： 国家自然科学基金重点项目（51837004）;云南省重大科技专项计划（202002AF080001）

作者简介： 谢一工（1972—），男，硕士，高级工程师，研究方向为电力系统调度运行与控制. E-mail：elfwu@21cn.com

引文格式： 谢一工，程旻，张孝，等.基于SFR模型的电网广义惯性分区评估方法研究［J］.江苏科技大学学报（自然科学版），202 38（5）：63-69.DOI：10.20061/j.issn.1673-4807.2024.05.010.

Research on generalized inertial partition evaluation methodof power grid based on SFR model

XIE Yigong1， CHENG Min1， ZHANG Xiao2， ZHANG Dan1， YAN Wenlin1， CHEN Qian3

（1.Yunnan Electric Power Dispatching and Control Center， Kunming 650011， China）

（2.Nanjing Nari-Relays Electric Co. Ltd.， Nanjing 211100， China）

（3.College of Energy and Electrical Engineering， Hohai University， Nanjing 210098， China）

Abstract：In recent years， the electronics dominated trend of power system is more obvious. On the one hand， with the adjustment of energy structure， a large number of new energy generation using power electronics interface is connected to the grid; on the other hand， with the development of energy-saving technology， load equipment has gradually become electronics dominated. However， due to the increasing proportion of power electronic equipment in the power grid， the capacity of the original synchronous generator and asynchronous motor has been weakened， and the safety and stability of power grid has been adversely affected. Therefore， based on SFR model， a partitioned evaluation method of generalized inertia of power systems is proposed in this paper， which will also be used to compare and evaluate the performance of the system before and after compensation. Firstly， a SFR generalized inertia partition model for the power grid is established to align with the trend of power electronics. Subsequently， simulation scenarios are employed to model the frequency curves of system partitions both before and after inertia compensation. The inertia time constant H is accurately determined through the application of a particle swarm optimization algorithm， and the corresponding inertia distribution uniformity index Dδ is calculated. A comprehensive evaluation of H and Dδ is then conducted， shedding light on the enhancement of inertia magnitude and the uniformity of inertia distribution. Finally， based on the evaluation results， compensation measures are further refined， the aforementioned parameter calculation steps are revisited until meeting the requirements of design evaluation. The correctness and applicability of the proposed models and corresponding evaluation methods are validated by simulation examples.

Key words：new power system， power electronic dominated， partition inertial， generalized inertial， evaluation method

随着电力系统中新能源接入的范围与比例越来越大，以及负荷中变频驱动的电动机比例越来越高，当前电力系统的总体旋转惯性及频率响应性能持续下降，且在实际运行中发生了若干严重的事故.另一方面，未来的电力系统发电侧与用电侧的区分日渐模糊，发电侧包含了大量的新能源发电电源，而负荷侧包含了大量分布式发电与储能等元件.可预见，电网的同步问题将日益复杂［1-5］，以同步发电机为观测对象的传统研究方式值得商榷.

惯性水平是电力系统运行是否稳定、应激能力是否强大的重要指标，主要表现为对电网频率和功率突变的抑制能力，而电力系统的频率是否维持稳定，主要和电网中发电机侧、负荷侧有功功率的平衡与否相关，在理想的电网运行状态下，电力系统的有功功率在稳定运行时始终保持送出和消耗二者之间的平衡.但是在电网实际的运行过程之中，发电机的出力、负荷的消耗等随机性因素的变动会造成频率的波动.此时如果没有惯性的支撑，系统的频率很有可能在极短的时间内跌落到一个较低的值，从而对发电机等设备的运行造成影响，进一步会使整个电力系统失稳，从而对电网的正常运行带来恶劣的影响.

新能源发电在功率平衡上可以起到代替常规同步发电机组的作用.但电力系统整体的惯性水平也受到了很大的影响［6-7］，转动惯性整体降低、对一次调频［8］的反应能力也变得更弱，维持电网动态运行稳定性的能力也容易变得不足.可见，新型电力系统的电力电子化程度越来越高改变了总体的惯性特征，因此以传统的分析方式去衡量电力系统的惯性水平是有局限的.

另一方面，电力电子控制的新能源电源与新型负荷具有很快的受控功率响应特性，可以补偿一部分虚拟的惯性作用.即未来电网的惯性响应形式将发生较大变化，但是如何将虚拟惯性融入现有的电网频率安全控制具有较高的难度.

现阶段，为了新能源电源规划更具有前瞻性、科学性以及约束性，提高电网的等效惯性水平，改善电网的频率响应，国内外专家和学者进行了大量的研究工作.文献［9］提出对储能进行定量的配置方法，针对储能系统对电力系统频率的控制，该方法能够对电力系统的功率波动产生抑制的作用，并对储能的容量大小设定了相关的置信水平，应用该方法可以提高电力系统的频率响应能力，并且增强电力系统的暂态稳定性.文献［10］针对惯性缺失引发的电压跌落，利用VSG的频率调节与控制作用，综合转动惯量的特性，应用了微分负反馈的思想，改善了系统的电压控制环节，从而增强系统对无功电压的支撑作用.文献［11］提出了对电力系统惯性兼具时间、空间不同角度的评估，从量化惯性指标的角度，用3种空间体系对惯性水平进行评估，并利用具体的电网案例验证与说明.

可见，针对未来新型电力系统，采用计及虚拟惯性的频率控制是维持安全稳定运行的必要基础，进而应对新型电力系统整体惯性水平做出精确评估，对整体惯性响应能力进行定量的表征.但目前多集中于从节点惯性的角度对电力系统惯性进行大致估计，难以在空间分布层面分析电力系统的惯性水平.此外，主要针对暂态问题采用案例分析居多，集中研究元件级的惯性性能，对于大电网来说过于细微，对电力系统整体惯性响应方面的研究较为欠缺.新能源并网后，电网的传统意义惯性更加薄弱、惯性的分布更加不均匀，粗略的估计已不适用于电力电子化的电力系统的建设与发展.这种变化趋势下，需要对电力系统的惯性支撑能力进行更加精细化的评估与分析研究.

为此，文中提出了一种基于系统频率响应（system frequency response，SFR）的电网分区惯性评估模型，可反映分区的惯性大小以及惯性分布均匀性，从而得出更合理的惯性评估结果.进而，提出一种电力系统广义惯性的分区评估方法流程，其评估结果用于分区惯性补偿前后的性能对比，从而为电网的分区惯性补偿提供依据.

1" 电力系统的广义惯性

1.1" 电力系统的传统惯性

传统意义上的惯性是指机械旋转惯性，比如当电力系统的频率和规定标准值产生偏差时，发电机的一次调频不能立即动作，在时间上有一定的延迟，惯性响应就会对功率进行调节干预，阻碍频率快速变化.

传统电力系统发电侧的惯性主要由同步发电机的旋转惯量构成，大量新能源与储能并网后，基于电力电子设备的控制，出现了各种虚拟形式的惯性.虚拟惯性可以作为系统等效惯性支撑［12-14］，而储能的作用可以进一步提供功率响应的平滑度，提升一次甚至二次调频的效果.负荷侧惯性也不可忽视，传统负荷侧的惯性主要是电动机的机械旋转惯性，这些共同构成了宏观层面电网的惯性.

惯性对电力系统的影响主要分为3个方面，如图1.一方面，惯性不足会给电力系统带来电能质量的振动、抖动，产生谐波、电力系统频率的畸变和波形的毛刺；另一个方面，惯性水平降低会造成电力系统暂态功角的摆动和励磁系统的不稳定性；此外，电网的惯性缺失会削弱电力系统的频率响应能力、对后续一次调频产生不利影响.由此可见，提高电力系统的惯性水平是电力系统能够维持安全稳定运行的重要保障.

1.2" 新型电力系统的广义惯性

考虑到随着电力电子技术在海量设备上的应用，未来难以对传统意义上的机械惯性进行大规模补偿，况且电力系统中的负荷自调节作用已不可忽略不计，所以更加需要关注广义惯性对电力系统的影响作用.

由于从单一元件的角度去考虑电力系统的惯性表达过于复杂，且横跨惯性响应和一次频率调节两个时间尺度，在运行机理上难以处理，所以需要用特定的模型来综合地描述电力系统的广义惯性.其目标是能够在较长的时间尺度下，用统一的模型表达电力系统的广义惯性特性，使其不仅可以应用于整体、还能用于分区，弱化和具体电力设备之间的关联，扩大模型的适用范围.

1.3" 分区评估的必要性

传统电网的机械旋转惯性主要分布在源端的同步发电机与末端的直连电动机，在不考虑网络中少量调相机与中小型机组的情况下，对惯性的分析评估是比较明确与准确的.

随着新型电力系统的建设与发展，源端发电机与末端电动机提供的传统惯性都明显下降，电网中被迫设置了越来越多的调相机，各种新能源电源与储能将越来越多的提供虚拟惯性控制，这些因素使得电网的惯性分析日益复杂.另一方面，未来新型电力系统的实际动态安全问题，其空间尺度也越来越小，越来越多产生局部性的频率安全问题.因此，不论从安全运行还是从建设规划而言，针对电网开展分区的惯性评估是十分必要的.

新型电力系统背景下，电力系统的整体惯性降低，且区域惯性薄弱的特点愈加突出，为了使惯性的分布更加均匀，需要对电力系统进行分区补偿.比如，虽然可以用调相机等设备进行补偿调节，但其设置成本与代价较高、且资源有限，目前在特高压直流落点附近加入调相机补偿仅是一种极端情况，为了改善惯性分布的均匀性，需在惯性薄弱处针对性设置，所以下文提出的综合评估方法来衡量这种补偿是否合理.

2" 电力系统分区的广义惯性评估流程

2.1" 广义惯性模型建立

电力系统频率响应模型中既需要计及发电机本体，又需要计及调速控制，以及负荷及其频率控制，所以SFR模型可以综合描述电力系统的惯性水平和频率响应能力，能够刻画出从扰动开始，直至一次调频、甚至到部分二次调频的时间尺度内的电力系统动态性能.

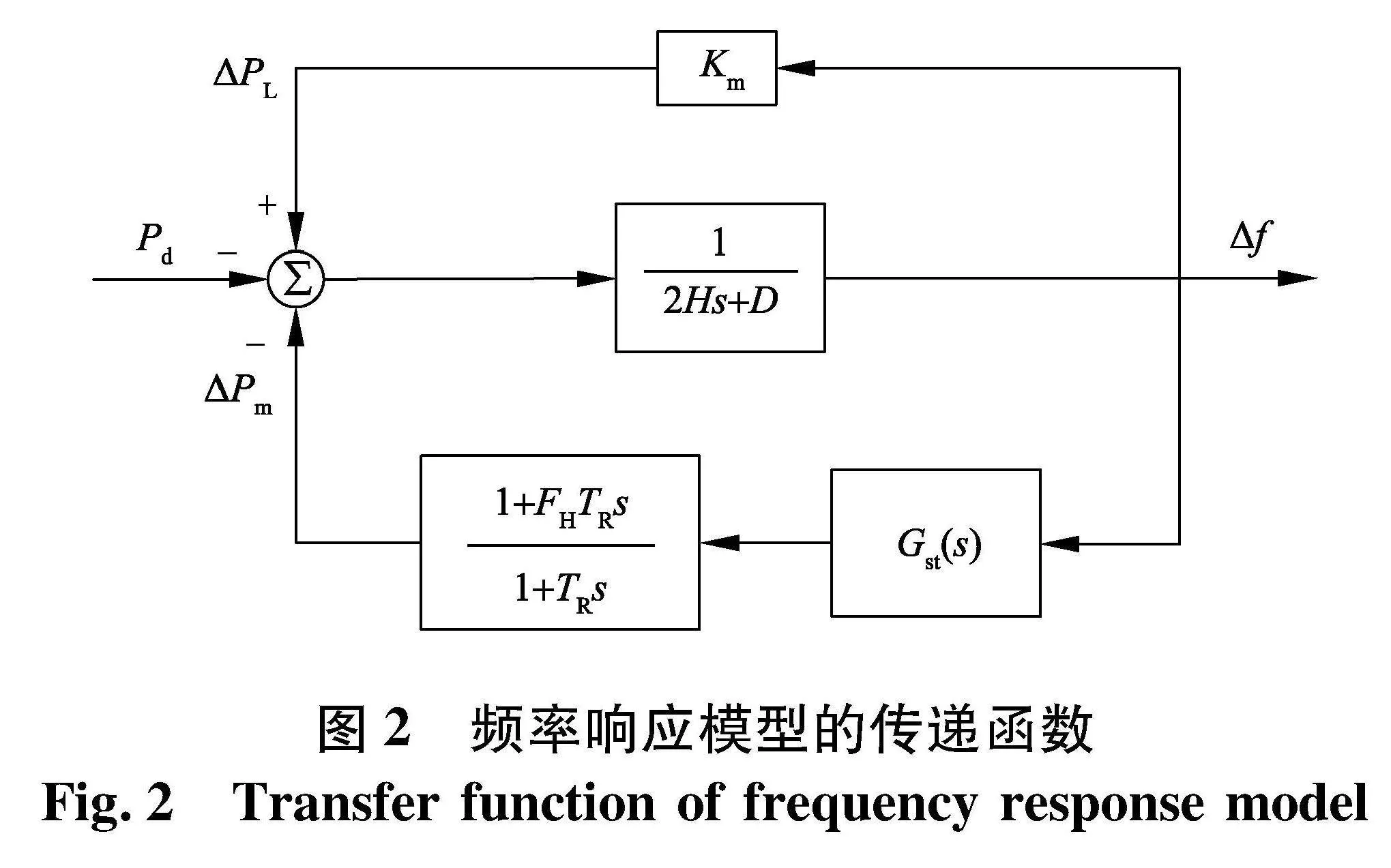
文中引入传统SFR模型［15］，如图 既可以用于电力系统整体也可以应用在具体分区中，各参数是电力系统已知的推荐参数，考虑将不确定的电力电子设备对电力系统的影响计入原有惯性时间常数H.

该模型原有的H用于在较长时间尺度内综合描述电力系统的广义惯性水平，文中沿用H表示电力系统的广义惯性时间常数，横跨了惯性响应和一次调频的时间尺度，淡化了海量元件级设备的具体特性.由于只计及海量新型设备的总体特性，因此可简化相关的计算过程与步骤，拓宽了模型的适用范围.

扩展了参数H的定义后，该频率响应模型既包含了发电机及其控制，也包含了负荷侧电力电子设备的控制，甚至也可计及网络中调相机等设备及其控制，因此可以用于表达新型电力系统的综合惯性水平.

2.2" 广义惯性评估指标

当受到外界小扰动或者大扰动的影响时，电力系统的功率出现差额，系统的惯性能够先于电力系统的一次调频瞬间动作于抑制频率突变、对频率进行调节，惯性响应的速度很快，可以在一次调频之前起到支撑系统频率稳定、协助后续一次调频更好运行的重要作用.

系统惯性主要由旋转电机的转动动能支撑，当发电机处在额定负载运行状态时，因此采用此时的发电机组动能与发电机组额定容量的比值作为指标来衡量惯性水平.

H=EkSB=J·ω22SB（1）

式中：H为惯性时间常数，为s；SB为机组的额定容量.由式（1）可知，惯性常数与发电机组的出力大小、是否出现扰动无关，当电力系统出现功率缺额的情况下，电力系统惯性时间常数值会影响电网频率的初始跌落速度、跌落的最低点、波动时间，与电力系统相应的重要指标均紧密相关.

当电网发生扰动时，功率和频率与标准值出现偏差，转子的旋转储能释放能量来补偿电网的功率缺失，通过测量系统功率和频率的变化，可以计算出该系统的惯性时间常数.惯性时间常数越大，转子越不容易迅速加速，发生超速的可能性越小，则该系统惯性水平越高、抵御扰动平滑系统频率的能力越强.

分析广义惯性分布均匀指数有利于在把握全网惯性的整体水平及其分布特征.对于新能源渗透率高的区域，也能更快地察觉其低惯性的特征，以便及时对此制定和实施调整惯性的策略，并有利于进一步对电网进行局部区域的具体分析，并在扰动发生后及时投入补偿装置，有利于提高系统运行频率的稳定性，增强对电网的调控能力.

为了兼顾发电侧和负荷侧的惯性分布情况，在惯性分布指数的基础上提出广义惯性分布均匀指数Dδ，将各分区的广义惯性时间常数Hi和容量Pi的比值设为Di，其中Pi的取值为发电容量和负荷容量的最大值为：

Pi=max{PGi，PLi}（2）

则各区Di的平均值为：

ED=∑ni=1Din（3）

则广义惯性分布均匀指数Dδ为：

Dδ=∑ni=1（Di－ED）2n（4）

经验表明，若广义惯性分布均匀指数Dδ值小于0.02则说明该系统的广义惯性平均性较好.

2.3" 广义惯性的分区评估流程

广义惯性的水平是衡量电力系统稳态和暂态稳定性的重要标准，广义惯性的评估是电网稳定与分析调节的基础.新能源发电和电力电子设备的比例越来越高，引起了电力系统的惯性支撑和动态响应能力发生了很大的变化，惯性区域化特征愈发明显.如此一来，对于现在这种电力电子化的电力系统不能以单一的角度来分析其惯性情况.原来在固定的运行状态用统一的指标去评估电网惯性是不再适用的，参考原电力系统整体惯性的评估方式.现在需要重新应用一个可以用于电网分区的广义惯性评估方法，从而适应大规模新能源并网后的电力系统，该广义惯性评估方法如图3.

文中考虑了电力电子化的新型电力系统的广义惯性分区，基于引入了电力系统频率响应模型（SFR模型），综合反映了电力系统惯性动态特性和频率响应能力，并利用该模型原有惯性时间常数H，表达电力系统的广义惯性时间常数.该模型既包含了传统旋转元件的转动惯量，同时又包含了常规状态下的系统控制效应，可评估电网最初扰动到系统一次调频期间、甚至部分二次调频时的系统惯性，在建立电力系统频率响应模型时，选择了相应的原动机、调速器的聚合模型.在PSASP和Matlab软件平台中搭建了相应的模型，通过仿真拟合并验证该模型及方法的正确性与适用性.

在SFR模型中，一共有6个参数，假定D、FH、TR、Km和Tst是系统固有参数已知，根据不同的广义惯性时间常数值，可以得到不同的频率响应曲线.文中利用粒子群算法拟合出广义惯性时间常数H的值［16］.

3" 算例分析

3.1" 评估模型的验证

为验证电力系统频率响应模型对电力电子化电力系统频率响应的适用性，利用 PSASP软件平台来搭建IEEE36节点仿真模型.除了依据城市区域的地理位置、行政范围、城市规模、规划布局、人口密度、负荷密度及负荷性质等外在客观条件来划分电力系统区域之外，从电力系统节点的角度研究电网的时候，还可以利用电力系统节点的特性和区域惯性特性进行电网区域的划分.依照电力系统节点的同调性及广义惯性水平对电力系统进行分区，将其分为3个区域：① 以传统发电机、负荷为主的区域；② 以新型负荷为主的区域；③ 传统负荷及新能源发电相融合的区域.

在发生扰动之后，不同区域机组转子运动存在差异、频率响应分布不同，从而造成惯性相对薄弱的区域.根据电力系统的节点特性和区域惯性特点对电网进行区域划分，可以将具有类似惯性特点的电力系统节点划分在同一区域内，在电力系统发生扰动时，其响应特性相近、从而可以对惯性薄弱的部分统一且有针对性地进行补偿，因而可以基于此分区结果进行进一步的电力系统广义惯性评估.

由图4可见，系统分为3个区域：含节点G1、G2的采用原有发电机与负荷模型的区域；含节点G5、G6的新型负荷为主的区域；以及含节点G3、G4、G7、G8的传统负荷与新能源发电相融合区域.并以此在PSASP软件中建立仿真模型获取系统仿真数据.

为了验证模型的正确性，进行了广义SFR模型的输出对比校核：一组是仿真的实测频率响应曲线，另一组为采用广义SFR模型的分区频率响应曲线.机电暂态过程中，各个节点的瞬时功角是不一样的，为了得到描述区域的广义惯性时间常数，文中采用了对区域内各个节点频率响应加权平均的方法，从而得到整个区域的广义惯性时间常数值.

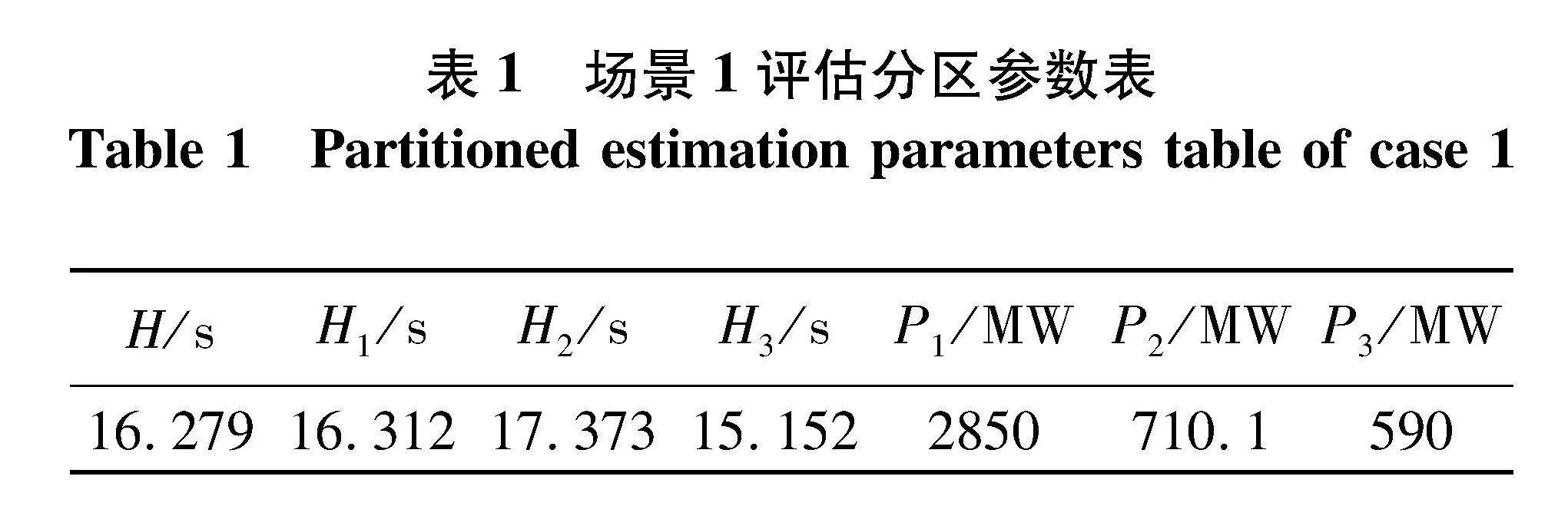
负荷功率扰动下，根据仿真实验得到场景1的广义惯性时间常数及分区容量参数，如表1.

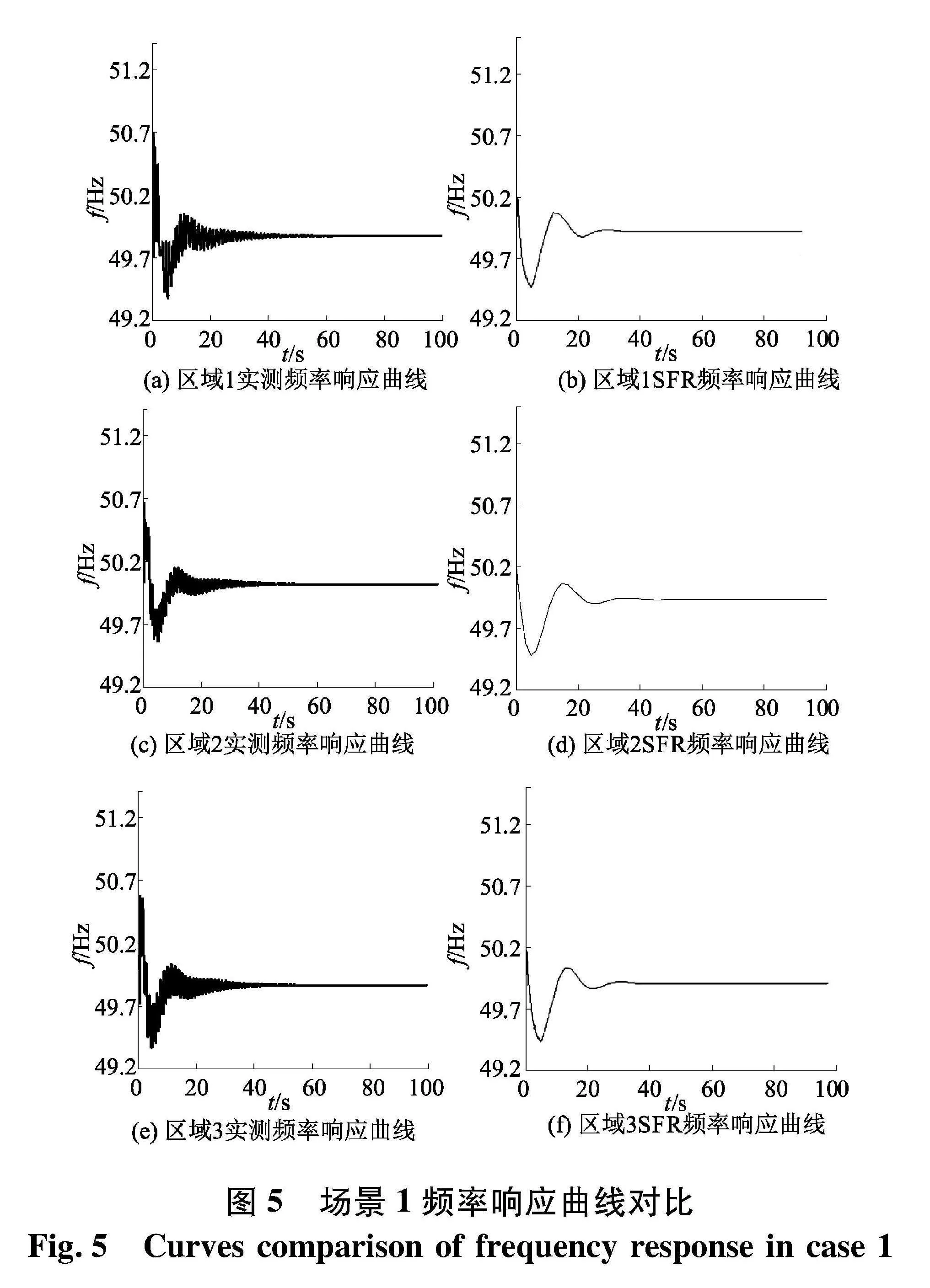
场景1下的仿真实测分区频率响应曲线以及SFR模型频率响应曲线对比如图5.

由场景1参数可得式（5）：

P1·H1+P2·H2+P3·H3P1+P2+P3=16.329（5）

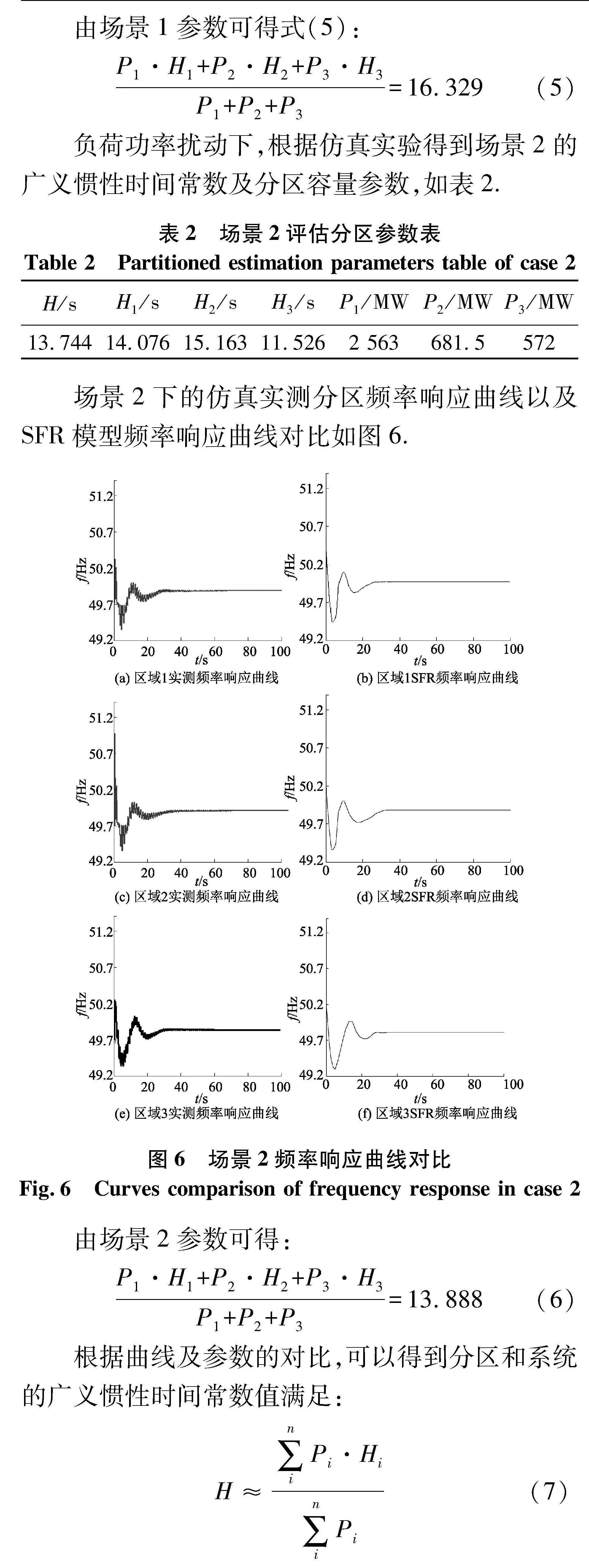
负荷功率扰动下，根据仿真实验得到场景2的广义惯性时间常数及分区容量参数，如表2.

场景2下的仿真实测分区频率响应曲线以及SFR模型频率响应曲线对比如图6.

由场景2参数可得：

P1·H1+P2·H2+P3·H3P1+P2+P3=13.888（6）

根据曲线及参数的对比，可以得到分区和系统的广义惯性时间常数值满足：

H≈∑niPi·Hi∑niPi（7）

式中：Pi的取值为发电容量和负荷容量的最大值.

通过相应的扰动测试，采用外部拟合的方法对模型的准确性与正确性进行了对比.可以看出该SFR模型的频率响应符合实际情况，且分区和系统的广义惯性时间常数值能够满足式（7）.

通过对比观察PSASP模拟实测频率响应曲线和SFR频率响应曲线的跌落、收敛过程，以及恢复稳定运行状态的过程，SFR模型输出曲线与模拟实测录波曲线均具有较好的拟合效果.对比频率响应曲线可知，该频率响应模型能够较好的拟合出电网的实测频率响应曲线，在一定程度上呈现出故障后系统的调频能力，并且可以反映出电力系统频率响应模型在目前大电网频率仿真领域的有效性，符合电力系统分析的宏观要求.

由此可见，该模型及其参数是合理的，因此可以用广义惯性时间常数H来表达电力系统的综合惯性，并且能够采用上述简化的系统模型去评估分区电力系统的广义惯性水平.

3.2" 惯性改善的对比分析

进而，为了针对电力电子化电力系统整体惯性下降、分布不均的特性，可以将该模型应用于电力系统广义惯性分区改善效果的评估.

由于区域3是传统负荷及新能源发电相融合的区域，可预见其相对惯性水平是最低的，因此在节点G7增设了调相机.补偿前后，基于SFR模型的分区频率响应曲线对比如图7.

通过对比补偿前后的分区频率响应曲线，可以看出补偿后，频率跌落的最低点有所提高，且频率恢复的时间更快，可见系统整体的频率响应都得到了改善.

对比图7（e）和图7（f），可以看出，整体频率响应改善的同时，局部惯性薄弱区域（区域3）的频率响应能力也得到了显著提高，在扰动发生初期能够为系统提供更大的惯量支撑.

假设广义惯性改善前系统的广义惯性时间常数为H 改善后系统的广义惯性时间常数为H 通过参数拟合后可知H1大于H 经过计算可得，在补偿后，系统的广义惯性分布均匀指数Dδ值小于0.0 满足安全要求.

通过观察其余各区域的频率响应曲线（图7（a、b、c、d））可知，经过局部补偿后系统整体的频率响应均得到了改善，全电网对于频率变化的抑制能力也因此更强，频率跌落的最低点有所缓和，频率波动的范围更小，其频率调节性能更加优良.

4" 结论

基于SFR模型提出了一种电力系统广义惯性的分区模型，及其相应的评估方法.通过设置广义惯性时间常数H和广义惯性分布均匀指数Dδ这两个广义惯性评估指标，反映电力系统广义惯性的大小及其分布均匀性，从而对电力电子化电力系统的广义惯性水平进行综合的评估.

通过基于SFR模型的分区频率曲线与模拟实测频率曲线对比，验证了所提模型的正确性；通过惯性补偿前后的对比，验证了提出评估方法的适用性与有效性.

未来新能源发电的渗透率进一步增大，使电网中风电、太阳能光伏、分布式电源等新型发电机组与传统的电力设备融合度大大提高，电力系统的结构更加复杂.现有评估方法仍不够合理，一方面需要从更全面、更多角度的指标对未来的电力系统惯性水平进行评估；另一方面，还需对其更进一步的针对未来电网的高弹性与多样性，并采取合理的颗粒度与尺度进行有效评估.

参考文献（References）

［1］" 桂林， 李岩军， 詹荣荣， 等. 大型调相机内部故障特征及纵向零序电压保护性能分析［J］. 电力系统自动化， 2019， 43 （8）： 145-149．

［2］" 武倩羽， 周莹坤， 李晨阳， 等. 新能源同步机并网系统惯性特性的理论和实验研究［J］. 大电机技术， 2019， 6 （1）： 41-46.

［3］" 张剑云， 李明节.新能源高渗透的电力系统频率特性分析［J］. 中国电机工程学报， 2020， 40 （11）： 3498-3506．

［4］" 刘杰锋，李冰， 张帆， 等. 电力系统频率特性影响因素研究及概述［J］. 电气应用， 2019， 38 （3）： 29-34.

［5］" 杨鹏， 刘锋， 姜齐荣， 等. “双高”电力系统大扰动稳定性：问题、挑战与展望［J］. 清华大学学报（自然科学版）， 2020， 21 （10）： 1-12.

［6］" 李兆伟， 吴雪莲， 曹路， 等. 抑制直流连续换相失败的调相机紧急控制［J］. 电力系统自动化， 2018， 42（22）： 91-97.

［7］" 赵博石， 胡泽春， 宋永华. 含直流馈入输电网中类调相机优化配置研究［J］. 电网技术， 2019， 43 （4）： 1151-1162．

［8］" 金一丁， 于钊， 李明节， 等. 新一代调相机与电力电子无功补偿装置在特高压交直流电网中应用的比较［J］. 电网技术， 2018， 42 （7）： 2095-2102.

［9］" 周晓华， 张银， 刘胜永， 等. 静止无功补偿器新型自适应动态规划电压控制［J］. 电力系统保护与控制， 2018， 46 （12）： 77-84．

［10］" 张彦凯， 魏久升， 史玉杰. 新型同步调相机动态无功特性分析研究［J］. 信息技术与网络安全， 2019， 38 （1）： 82-86.

［11］" JIA Jundi， YANG Guangya. Investigation on the combined effect of VSC-based sources and synchronous condensers under grid unbalanced faults［J］. IEEE Transactions on Power Delivery， 2019，34（5）：1898-1908.

［12］" 郭小龙， 刘方蕾， 胥国毅， 等. 风电机组参与调频的虚拟惯量控制与快速频率控制［J］. 智慧电力， 2020， 48 （12）： 1-7.

［13］" 唐晓骏， 蔡继朝， 马世英， 等. 双馈风电并网对电力系统频率响应的影响［J］. 电力系统及其自动化学报， 2020， 32 （10）： 37-43.

［14］" 杨亚枢. 虚拟惯量控制对提高电网一次调频稳定性的影响［J］. 大功率变流技术， 2016， 6 （1）： 52-54.

［15］" 李东辉， 臧晓明， 鞠平， 等. 电力系统频率响应的改进模型与参数估计［J］. 电力工程技术， 2019， 38 （5）： 85-90.

［16］" 朱永，李春华. 基于多目标粒子群算法的微电网优化运行研究［J］. 江苏科技大学学报（自然科学版）， 2017， 31（4）： 501-507.

（责任编辑：曹莉）