基于粒球的三支聚类方法

摘" 要： 针对硬聚类中样本均被强制划分到一个类簇，没有考虑信息具有不确定性而导致决策风险提高的问题，将粒球与三支聚类结合，提出了一种基于粒球的三支聚类算法.通过对每一个数据簇建立一个粒球模型，以自适应的方式为每个粒球寻找其近邻粒球.根据近邻粒球的情况来将粒球划分为稳定域与活动域，以赋予不同的权重将稳定域与活动域中的样本数据进行更新迭代.稳定域被认定为该类的核心域，活动域为该类的边间域.采用不同的UCI数据集进行实验，实验结果表明：所提算法较好的解决了不确定性信息对于决策风险提高的问题，验证了该算法的有效性.

关键词： 三支聚类；粒球；稳定域；活动域

中图分类号：TP391""" 文献标志码：A""""" 文章编号：1673-4807（2024）05-057-06

DOI：10.20061/j.issn.1673-4807.2024.05.009

收稿日期： 2023-07-12""" 修回日期： 2021-04-29

基金项目： 国家自然科学基金项目（62076111， 61773012）；江苏省高校自然科学基金项目（15KJB110004）

作者简介： 韩兴雨（2000—），男，硕士研究生

*通信作者： 孟义平（1979—），女，副教授，研究方向为应用数学、三支决策.E-mail：ypmeng@just.edu.cn

引文格式： 韩兴雨，朱金，孟义平，等.基于粒球的三支聚类方法［J］.江苏科技大学学报（自然科学版），202 38（5）：57-62.DOI：10.20061/j.issn.1673-4807.2024.05.009.

Three-way clustering based on granular-ball

HAN Xingyu1，ZHU Jin2，MENG Yiping 2*， WANG Pingxin2

（1.School of Computer， Jiangsu University of Science and Technology， Zhenjiang 212003， China）

（2.School of Science， Jiangsu University of Science and Technology， Zhenjiang 212100， China）

Abstract：In order to solve the problem of traditional clustering where samples are forcibly divided into one cluster without considering information uncertainty， thereby increasing decision risk. In this paper， a three-way clustering algorithm based on granular-ball is proposed by combining granular-ball with three-way clustering. The algorithm establishes a granular-ball model for each data cluster， and finds its neighboring granular-ball for each granular-ball in an adaptive way. The granular-ball is divided into stable area and active area according to the situation of the neighboring granular-ball， and then the sample data in the stable area and active area are updated and iterated by giving different weights. The stable area is identified as the core region of this class， and the active area is the fringe region of this class. Experiments are conducted using different UCI datasets， and the experimental results show that the proposed algorithm effectively solves the problem of increasing decision risk due to uncertain information， verifying the effectiveness of the algorithm.

Key words：three-way clustering， granular-ball， stable area， active area

聚类分析在数据挖掘和机器学习领域有着广泛的应用，如图像处理［1］、目标检索［2］等.传统的聚类方法其大多属于硬聚类，样本所在的类簇之间有着清晰的边界，不存在既属于一个类簇又属于另外不同类簇的对象.在实际处理中，考虑到不确定性信息的情况，将样本中的对象强制划分到一个类簇当中的决策是抱有风险的.认识到传统聚类方法的局限性，文献［3］提出三支决策聚类，通过将类簇划分为核心域、边界域和琐碎域来有效的降低信息不充分时的决策错误率，有效提高了聚类结果的可解释性.

三支聚类［4］用核心域和边界域来描述一个簇.这两个域将数据集分成3个部分，分别对应了3种隶属关系：属于，不属于和可能属于.三支聚类自提出以来，得到快速发展取得了大量的成果［5-8］.文献［9］针对聚类集成的样本稳定性概念，发现了稳定关系的样本集，提出基于样本稳定性的集成聚类方法.文献［10］将数学形态学中腐蚀和膨胀思想引入聚类，给出一种基于收缩和膨胀的三支聚类框架，解决了簇类划分中阈值固定的问题.

粒计算是将信息粒化以不同粒度解决问题的方法.粒化可从构建或分解的方向进行，将底层的粒合并为更高的粒是构建，反之则是分解.文中引入多粒度中粒计算与聚类中簇构成的粒球模型［11-12］，提出基于粒球的三支聚类方法.凭借数据簇构建的粒球及其近邻粒球，将通过近邻粒球判断出的粒球稳定域定义为核心域，活动域则定义为边界域.

1" 预备知识

1.1" 三支聚类

若给定包含n个样本对象的数据集U={x1，x2，...，xn}，聚类数为k，则传统硬聚类的聚类结果是C={C1，C2，...，Cn}，其中任意类簇满足：

Ci≠""" i=1，…，k∪ki=1Ci=UCi∩Cj=i≠j

在上述条件下，整个样本被划分成的类簇中不存在空集，不同类簇中也不存在公共元素.每个样本对象都被强制划分到一个类簇当中，其所在的类簇间具有清晰的边界.但信息具有不确定性，则将样本对象强制划分到一个类簇当中会降低聚类结果的质量.为了解决传统聚类方法的弊端，将三支决策思想引入到聚类中，将一定属于某个对象的元素置于核心域Co（Ci）内，将不确定的元素置于边界域Fr（Ci）内，琐碎域Tr（Ci）则代表一定不属于某个对象的元素.由此，一个类中的样本对象与簇的关系则被分为：一定属于该类簇、一定不属于该类簇和可能属于该类簇.

当满足以下条件：

Co（Ci）∪Tr（Ci）∪Fr（Ci）=U

Co（Ci）∩Tr（Ci）=

Co（Ci）∩Fr（Ci）=

Fr（Ci）∩Tr（Ci）=

数据集U的三支聚类表示结果为：

C={（Co（C1），Fr（C1）），（Co（C2）），Fr（C2））…，（Co（Ck），Fr（Ck））}

若Fr（Ci）=，则簇类被划分Co（Ci）和Tr（Ci）=U－Co（Ci）.三支聚类则变成为硬聚类.

1.2" k-means算法

k-means算法首先随机地选择k个数据对象，将其作为初始类簇中心.对剩余的数据，依据每个数据与其类簇中心的的距离，分配给与之距离最近的类簇.接着计算各个类簇中数据的平均值作为新的聚类中心，不断重复以上过程，其最终结果是将无标签的数据集自动划分成独立且紧凑的k个类簇.

1.3" 粒球的生成与稳定域和活动域的划分

在执行k-means算法后，数据会以欧氏距离为相似度指标，将每个数据对象划分置与其距离最近的类簇内.每个数据对象都包含在以聚类中心为形心，距离聚类中心最远数据到形心的距离为半径的区域内.

定义1" 在包含n个样本对象的数据集U={x1，x2，...，xn}中，对于任意一个粒球Ci，当前粒球的球心定义为：

ci=1Ci∑x∈Cix（1）

式中：|Ci|为当前粒球Ci中的样本数量；x为当前粒球Ci中的样本.

定义2" 对于任意一个粒球Ci，粒球Ci的半径定义为：

ri=max{dist（x，ci）|x∈Ci}（2）

式中：dist（）为x与ci之间的欧氏距离；x为当前粒球Ci中的样本；ci表示为粒球Ci的球心.具体情况如图 其中三角形代表粒球球心，圆形代表粒球中的样本.

定义3" 给定任意两个粒球Ci与Cj.其中ci和cj分别表示粒球Ci与Cj的球心，ri表示为粒球Ci的半径，若满足以下条件：

rigt;12‖ci－cj‖（3）

则称Cj为Ci的近邻粒球.

由定义3可知，若满足条件rigt;12‖ci－cj‖，则称Cj为Ci的近邻粒球.但此近邻关系不具备对称性.若Cj为Ci的近邻粒球，但不一定同时满足Ci为Cj的近邻粒球的情况.因此，任意两个粒球Ci与Cj的近邻关系可分为以下3种：

（1） 粒球Ci与Cj互为近邻粒球；

（2） 粒球Ci为Cj的近邻粒球，但Cj不为Ci的近邻粒球；

（3） 粒球Ci与Cj互不为近邻粒球；

具体情况如图2.

图2中，直线为两粒球球心的连线，虚线为两粒球球心连线的中垂线位置.以粒球C1为例，C1与C2互为近邻粒球；C3为C1的近邻粒球，但C1不为C3的近邻粒球；粒球C1与C4互不为近邻粒球.

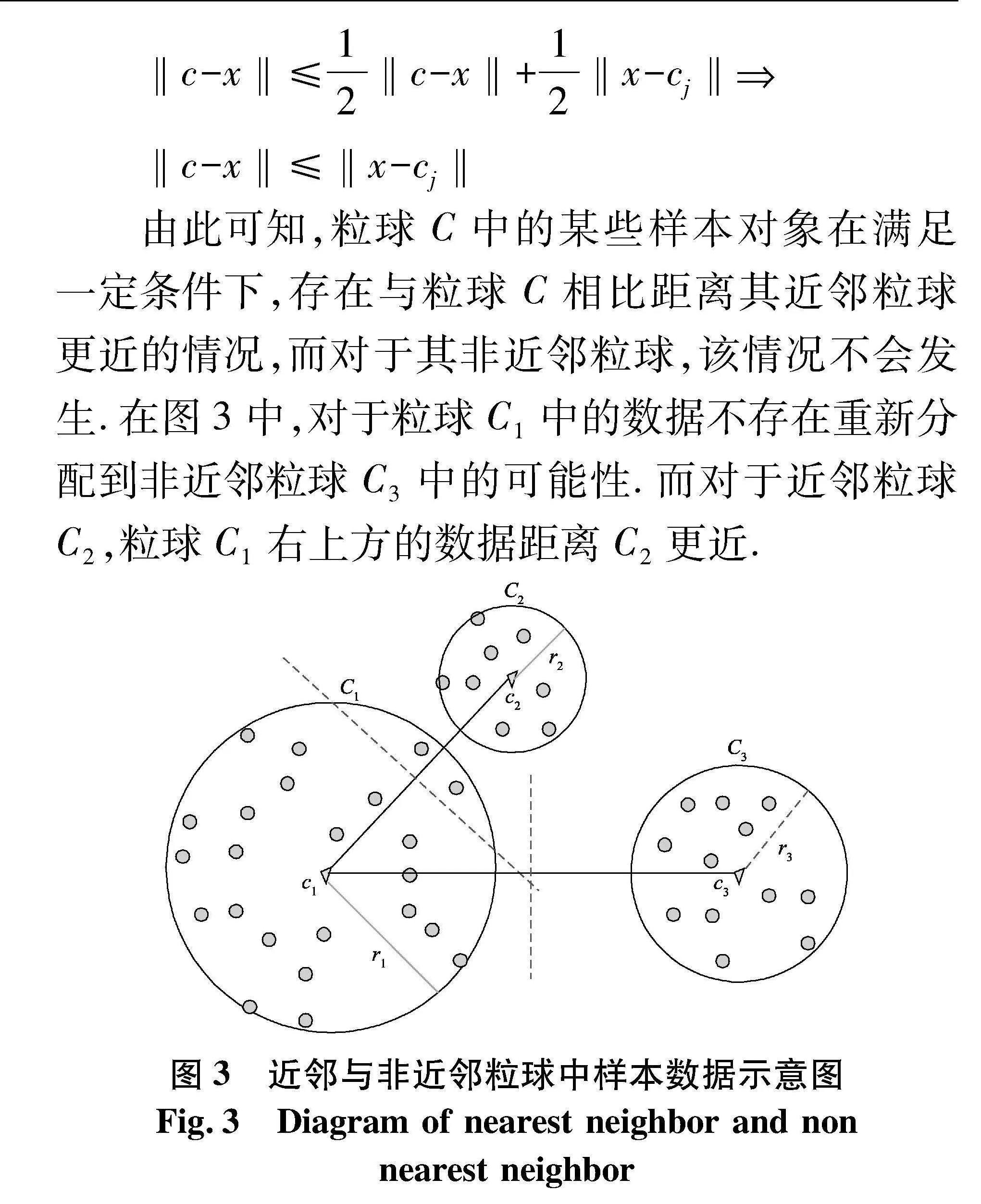
定理1" 给定任意两个粒球Ci与Cj，ci和cj分别表示粒球Ci与Cj的球心.若Ci为粒球C的近邻粒球，则粒球C中的数据样本存在被调整到粒球Ci中的可能性.若Cj不为粒球C的近邻粒球，则粒球C中的数据样本不存在被调整到粒球Ci中的可能性.

证明：设粒球C的半径为r，球心为c.

（1） 若Ci为粒球C的近邻粒球，则rgt;12‖c－ci‖.又r=max{dist（x，c）|x∈C}，x为当前类簇中的样本对象.则必定x∈C，使得‖x-c‖gt;12‖c－ci‖.假设此数据样本x位于线段cci上，则有‖x-c‖+‖x－ci‖=‖c－ci‖.则‖x-c‖gt;12‖x-c‖+12‖x－ci‖，即‖x-c‖gt;‖x－ci‖.

（2） 若Cj不为粒球C的近邻粒球，则r≤12·‖c－cj‖.又在粒球C中，x∈C，‖c－x‖≤r，则有

‖c－x‖≤r≤12‖c－cj‖=12‖c－x+x－cj‖≤

12‖c－x‖+12‖x－cj‖

‖c－x‖≤12‖c－x‖+12‖x－cj‖

‖c－x‖≤‖x－cj‖

由此可知，粒球C中的某些样本对象在满足一定条件下，存在与粒球C相比距离其近邻粒球更近的情况，而对于其非近邻粒球，该情况不会发生.在图3中，对于粒球C1中的数据不存在重新分配到非近邻粒球C3中的可能性.而对于近邻粒球C 粒球C1右上方的数据距离C2更近.

定义4" 给定任意一个粒球Ci，其近邻粒球球心的集合为{Nci}.若{Nci}≠，则对于球心集合内的所属任意粒球Cj，球心cj∈{Nci}，有以ci为球心，12min（‖ci－cj‖）cj∈{Nci}为半径所覆盖的“稳定域”，将粒球Ci中除稳定域以外的区域定义为“活动域”.若{Nci}=，则整个粒球Ci都为“稳定域”.具体情况如图4.

如图 粒球C1的近邻粒球球心集合为{Nc1}={c2}，不为空集.则存在以c1为球心，半径为12c1c2所覆盖成的“稳定域”.

定理2" 在当前的迭代轮次中，粒球中稳定域所覆盖的样本数据无需与其他任意粒球比较到各自球心的距离.

证明：给定任意一个粒球Ci，其近邻粒球球心的集合为{Nci}.设x为粒球Ci稳定域中的任意样本数据.则有：

‖x-ci‖≤12min（‖ci－cj‖）cj∈{Nci}≤12（‖ci－x‖）+

12min（‖x－cj‖）cj∈{Nci}

‖x-ci‖≤12（‖ci－x‖）+12min（‖x－cj‖）cj∈{Nci}

‖x-ci‖≤min（‖x－cj‖）cj∈{Nci}.

综上所述，在确定粒球Ci的“稳定域”后，其所在范围内的任意数据，在本轮的迭代次序中无需与其他任何粒球中的样本对象比较到各自球心的距离.即粒球Ci的“稳定域”内所覆盖的样本对象距离所属球心ci是最近的.

2" 基于粒球的三支聚类算法

2.1" 粒球模型的建立与近邻粒球的搜索

在输入数据集后，由包含n个样本对象的数据集U={x1，x2，...，xn}在进行一次k-means迭代过程后，将原本的数据集U划分成k个簇类：U={V1，V2，...，Vk}，形成初始的聚类结果.而任意类簇Vi内的样本对象都被包含在以其聚类中心为形心，距离形心的最远数据到形心的距离为半径的覆盖区域内.因此，可将任意类簇Vi转化成粒球Ci，则数据集U进一步划分成为由粒球构成的k个簇类：U={C1，C2，...，Ck}.其球心ci的定义如式（1），半径ri如式（2）.

在迭代过程当中，为了避免当k值过大时所引发的大量不必要的距离计算，根据式（3）判断粒球C的近邻与非近邻粒球来对数据进行预处理.由定理1可知，若Ci为粒球C的近邻粒球，则在粒球C中，可能存在距离Ci更近的数据样本.说明粒球C中的数据样本存在被调入到Ci的可能性，这一部分的数据计算是必要的.但若Cj不为粒球C的近邻粒球，则位于粒球C中的数据样本到C的距离均小于等于到Cj的距离.即粒球C中的数据样本无需调整到非近邻粒球当中去，由此可减少了一部分冗余的计算量.

2.2" 粒球的更新

将由进行一次k-means迭代所生成的初始聚类结果构成相应的粒球模型，通过搜索粒球对应的近邻粒球来避免不必要的冗余计算与划分不同区域.这一步将对粒球中的样本数据进行更新.

对于以欧式距离作为相似度指标所形成的任意粒球Ci，其“活动域”中的数据可能存在距离相应近邻粒球更近的情况，所以仍需计算到各个近邻粒球球心之间的距离，按就近原则分配到相应的粒球当中，并且进行数据更新过后的粒球也必须按定义1和定义2重新构建粒球模型.鉴于其“稳定域”内的样本数据在本次迭代过程中不会调整到其他粒球内，这部分数据所构成的类簇具有较好的独立且紧凑的特性，因此赋予较大的权重wCo（Ci）.而更新后的“活动域”中的样本数据则与之相反，赋予较低的权重wFr（Ci）′，其中wCo（Ci）0. wCo（Ci）+wFr（Ci）′=1.则粒球Ci的球心ci′以及半径ri′更新具体表示为：

ci′=wCo（Ci）∑x∈Co（Ci）x+wCo（Ci）∑x∈Fr（Ci）′xwCo（Ci）Co（Ci）+wFr（Ci）′Fr（Ci）′（4）

ri′=max{dist（x，ci′）|x∈Co（Ci）∪Fr（Ci）′}（5）

式中：Co（Ci）为粒球Ci“稳定域”中的样本数量；Fr（Ci）′为原“活动域”中的样本对象进行重新就近分配后的新“活动域”中的样本数量.

2.3" 粒球区域的划分

由定义4可知，给定任意一个粒球Ci，通过判断其近邻粒球的情况，可以将整个粒球Ci所覆盖的区域分成“活动域”与“稳定域”.而根据定理2的证明，在粒球Ci“稳定域”中的任意样本数据x到球心ci的距离，均小于等于其到任意近邻粒球球心的距离.即当前迭代过程中，粒球“稳定域”中的样本无需进行调整.

由此，为了刻画数据的不确定性，把粒球Ci“稳定域”定义为该类簇的核心域Co（Ci），具体表示为：

Co（Ci）={x∈U|x∈Ci∧dist（x，ci）≤

12min（‖ci－cj‖）cj∈{Nci}}（6）

将“活动域”定义为该类簇的边界域Fr（Ci），具体表示为：

Fr（Ci）={x∈U|x∈Ci∧dist（x，ci）gt;

12min（‖ci－cj‖）cj∈{Nci}}（7）

将其余区域定义为该类簇的琐碎域Tr（Ci），具体表示为：

Tr（Ci）=U－Co（Ci）－Fr（Ci）（8）

经过以上操作，得到了该类簇基于粒球Ci所划分成的核心域、边界域和琐碎域.则数据集U的三支聚类表示为：

C={（Co（C1），Fr（C1）），（Co（C2），Fr（C2））…，（Co（Ck），Fr（Ck））}

2.4" 基于粒球的三支聚类（3WG）算法流程

基于粒球的三支聚类算法基本思想是采用多粒度中粒计算与聚类中簇构成的粒球模型，凭借粒球模型做出不同的区域划分以此更新迭代其中的样本数据.即对原始数据进行粒球建模，由其相应的近邻粒球减少不必要计算的同时区分出粒球中的“稳定域”与“活动域”.首先对数据进行一次k-means迭代，由初始聚类结果得出相应的粒球模型.其次便是通过粒球模型寻找其近邻粒球来划分出粒球中的不同区域，无需重新计算分配稳定域中的数据.对于“稳定域”中的数据样本赋予较大的权重，“活动域”与之相反，这样在迭代过程中可以有效降低活动域中的数据重新分配与粒球模型的更新对聚类结果的影响.为了较好的刻画数据的不确定性，对每个类簇进行粒球建模所划分成的“稳定域”与“活动域”得到每个类的核心域和边界域，由此获得数据集的三支聚类结果.算法1给出了基于粒球的三支聚类算法流程.

算法1 ： 3WG算法

输入：" 数据集U，簇数目k，权重w

输出：

C={（Co（C1），Fr（C1）），（Co（C2），Fr（C2））…，（Co（Ck），Fr（Ck））}

1．完成一次标准的k-means迭代

2．根据初步的聚类结果，根据公式（1）、（2）构建出粒球模型

3. 设置迭代次数n

4. repeat

5. for i=1... k" ∥ 对每个粒球进行遍历

6. 通过rigt;12‖ci－cj‖判断粒球Ci的近邻粒球

7. 对粒球Ci以12min（‖ci－cj‖）cj∈{Nci}为半径，ci为球心构成“稳定域”.其余区域中的样本数据构成“活动域”并按距离就近分配到其余粒球

8. 更新除粒球Ci之外，被新分配样本数据的粒球.其球心不变，更新半径及其所属数据.

9. 根据式（4）、（5）更新粒球Ci的球心与半径

10. until 所有的球心不再发生变化或迭代次数达到事先设定的阈值

11. 提取Co（Ci）={x∈U|x∈Ci∧dist（x，ci）≤

12min（‖ci－cj‖）cj∈{Nci}}，得到Ci的核心域

12. 提取Fr（Ci）={x∈U|x∈Ci∧dist（x，ci）gt;12min（‖ci－cj‖）cj∈{Nci}}，得到Ci的边界域

13. 得到最终聚类结果：

C={（Co（C1），Fr（C1）），（Co（C2），Fr（C2））…，（Co（Ck），Fr（Ck））}

3" 实验分析

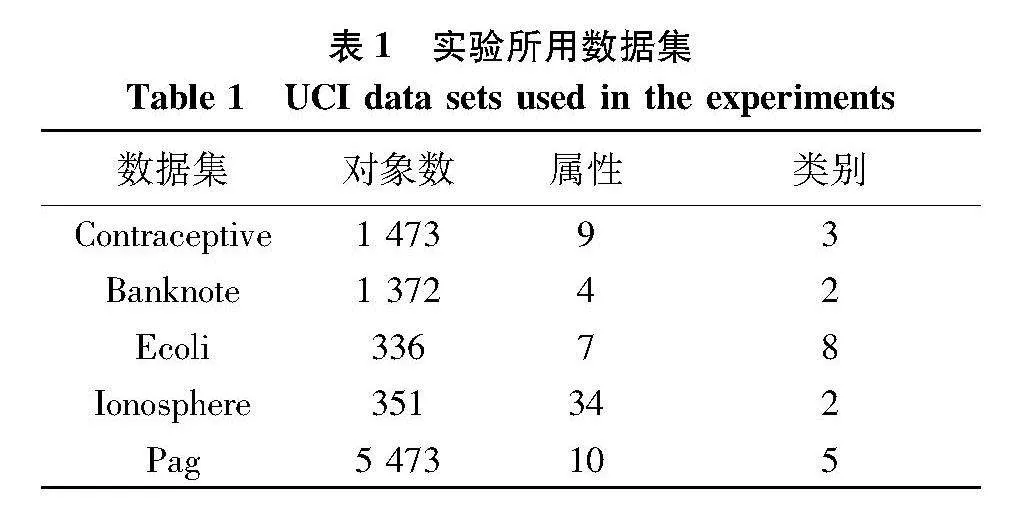
为了验证3WG算法的有效性，采用了5组UCI数据进行实验，数据集信息如表 将基于粒球的三支聚类算法与传统的聚类k-means和谱聚类进行SC、DBI和ACC聚类指标的对比.

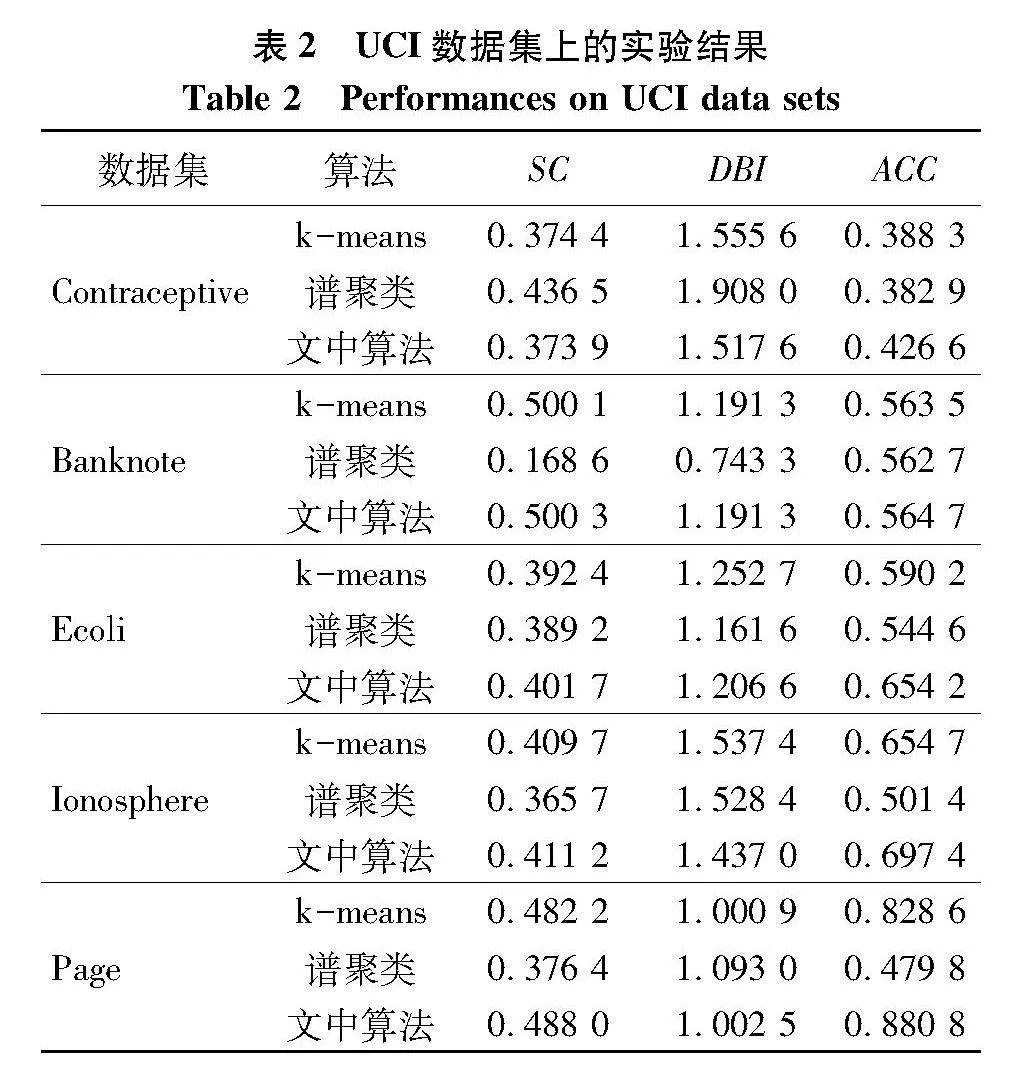
将每个类簇的稳定域作为核心域，活动域作为边界域获得数据集的三支聚类结果并计算聚类指标SC、DBI和ACC.SC的范围为［- 1］，同类别样本距离越相近不同类别样本距离越远，SC值越高，其中负值代表该样本数据不应被分配到该类的程度，正值则与之相反，零表示样本刚好位于两个不同类簇之间.DBI与ACC指标值域为［ 1］，DBI越小意味着类内距离越小，同时类间距离越大.ACC越大表示算法的聚类结果与真实聚类结果越接近.实验结果如表2.

为了进一步验证该算法的有效性，将算法得到核心域内的数据标签与真实标签做对比.表3为仅计算聚类结果中核心域内数据的准确率与整个类簇准确率在聚类指标SC、DBI和ACC上的对比结果.

观察表2、3的数据对比结果，通过比较SC的值可以发现，算法3WG在大多数数据集上表现出来的性能都优于其他2个算法.以数据集Ionosphere为例，在通过3WG算法进行聚类后SC的值为0.411 2.利用k-means算法和谱聚类算法进行聚类后，SC的值分别为0.409 7和0.365 7.轮廓系数SC的值代表着所有样本轮廓系数的平均值，当同类别的样本越近，不同类别的样本越远时值越大.而3WG算法中通过构建粒球模型划分类簇，通过赋予核心域较大权重，边界域赋予较小权重进行数据更新，使聚类之间的分离程度得到提高，聚类内的分散程度得到降低.观察DBI的值可以发现，3WG算法在Banknote上没有达到预期结果，在其他数据集上得到较好的值.这是由于DBI越小则表示类内距离越小同时类间距离越大，而粒球模型中的数据是以聚类中心为球心，到球心距离最远的样本到聚类中心的距离为半径所覆盖的区域，其三支聚类结果的表示在不同粒球间存在重叠区域.而比较ACC的值不难得出，3WG算法在大多数数据集上的表现都胜于其他2个算法.再将粒球中的稳定域作为整个类簇计算聚类评价值时，发现ACC在大多数据集上都有提升.

综上所述，3WG算法能较好地对具有不确定信息的数据进行聚类，其三支聚类的结果能更好地展现出聚类结构，改善聚类性能.

4" 结论

文中将多粒度中粒计算与聚类中簇构成的粒球模型与三支聚类进行结合，给出了一种基于粒球的三支聚类方法，通过构建的粒球模型寻找其近邻粒球，在减少了冗余计算的同时凭借近邻粒球的情况将粒球划分成不同区域.粒球的“稳定域”作为核心域，“活动域”作为边界域，从而获得类簇的三支聚类结果.实验结果表明，通过赋予不同区域不同的权重，以加权平均值的方式迭代球心及其样本数据，使聚类之间的分离程度得到提高，并且聚类内的分散程度得到降低，提升了聚类的各项性能.该算法中仍存在需要改进的地方，如三支聚类结果的表示在不同粒球间存在重叠区域，这种情况会使不同类簇间的聚集程度得到提高，降低了聚类结果的质量.另外，如何丰富参数的设置来更好地提取数据的特征也是未来研究的内容之一.

参考文献（References）

［1］" DING W， LIU Z， ZHANG F， et al. Research on visual image processing and edge detection method of micro flapping wing flying robot based on cluster analysis［C］∥Seventh Asia Pacific Conference on Optics Manufacture and 2021 International Forum of Young Scientists on Advanced Optical Manufacturing （APCOM and YSAOM 2021）. USA：SPIE， 2022， 12166： 493-500.

［2］" LAO G， LIU S， TAN C， et al. Three degree binary graph and shortest edge clustering for re-ranking in multi-feature image retrieval［J］. Journal of Visual Communication and Image Representation，2021，80：103282.

［3］" YAO Y. Three-way decisions with probabilistic rough sets ［J］. Information Sciences，2010，180（3）：341-353.

［4］" YU H. A framework of three-way cluster analysis［C］∥Proceedings of the Rough Sets. Poland： Springer， 2017：300-312.

［5］" YU H， ZHANG C， WANG G. A tree-based incremental overlapping clustering method using the three-way decision theory ［J］. Knowledge-Based Systems， 2016， 91： 189-203.

［6］" 施虹， 杨鑫，王平心.改进的均值插补不完备数据聚类算法［J］.江苏科技大学学报（自然科学版），2020，34（4）： 51-56.

［7］" YU H， CHEN L Y， YAO J T. A three-way density peak clustering method based on evidence theory［J］. Knowledge-Based Systems， 2021， 211：106532.

［8］" 凡嘉琛， 王平心， 杨习贝. 基于三支决策的密度敏感谱聚类［J］. 山东大学学报（理学版），2022， 57（11）：10-17.

［9］" 李飞江，钱宇华，王婕婷，等.基于样本稳定性的聚类方法［J］.中国科学：信息科学，2020，50（8）：1239-1254.

［10］" WANG P， YAO Y. CE3： A three-way clustering method based on mathematical morphology ［J］. Knowledge-Based Systems， 2018， 155： 54-65.

［11］" JI X， PENG J H， ZHAO P， et al. Extended rough sets model based on fuzzy granular ball and its attribute reduction［J］. Information Sciences，202 640：119071.

［12］" PENG X， WANG P， XIA S， et al. VPGB： A granular-ball based model for attribute reduction and classification with label noise［J］. Information Sciences， 2022， 611： 504-521.

（责任编辑：曹莉）