基于S曲线的数字阀步进电动机加减速控制方法

摘要：目前在控制步进电动机加减速过程中，存在最大加速度与最大减速度相差过大等问题。为此研究基于S曲线的数字阀步进电动机加减速控制方法，阐述基于S曲线构建数字阀步进电动机控制模型、数字阀步进电动机加减速阶段与匀速阶段的控制方法。通过对比实验证明，应用基于S曲线的数字阀步进电动机加减速控制方法，能够精确地控制步进电动机的转速，减少步进电动机的冲击和振动，提高工程施工的精度和效率。

关键词：数字阀步进电动机；S曲线控制模型；加减速；对比实验

0 引言

在工程施工领域，步进电动机作为一种常用的动力装置，在各类机械系统中得到了广泛的应用。步进电动机的特点是通过对脉冲个数、频率的控制，实现对转角、转速的准确控制，能够适应多种复杂的施工需要[1]。然而在施工过程中，如何实现步进电动机加减速的精确控制，仍然是一个关键问题。在工程施工领域，步进电动机的加减速控制方法往往会影响到施工精度和效率。以往步进电动机加减速，通常采用阶梯型曲线或指数型曲线控制方法。这些控制方法虽然简单易行，但存在控制不精确、最大加减速相差过大、冲击力大等问题，容易造成施工过程中的误差和设备损坏。如何实现步进电动机加减速的精确控制，对提高施工精度和效率具有重要意义[2]。因此，本文结合S曲线开展对数字阀步进电动机加减速控制方法的研究。

1 基于S曲线构建步进电动机控制模型

1.1 建立六段S曲线控制模型的方法

基于S曲线建立数字阀步进电动机加减速控制模型，需要明确控制对象、控制精度和控制范围参数，并根据控制目标和系统特性设计合适的S曲线。根据S曲线和电动机动力学方程，建立数学模型。

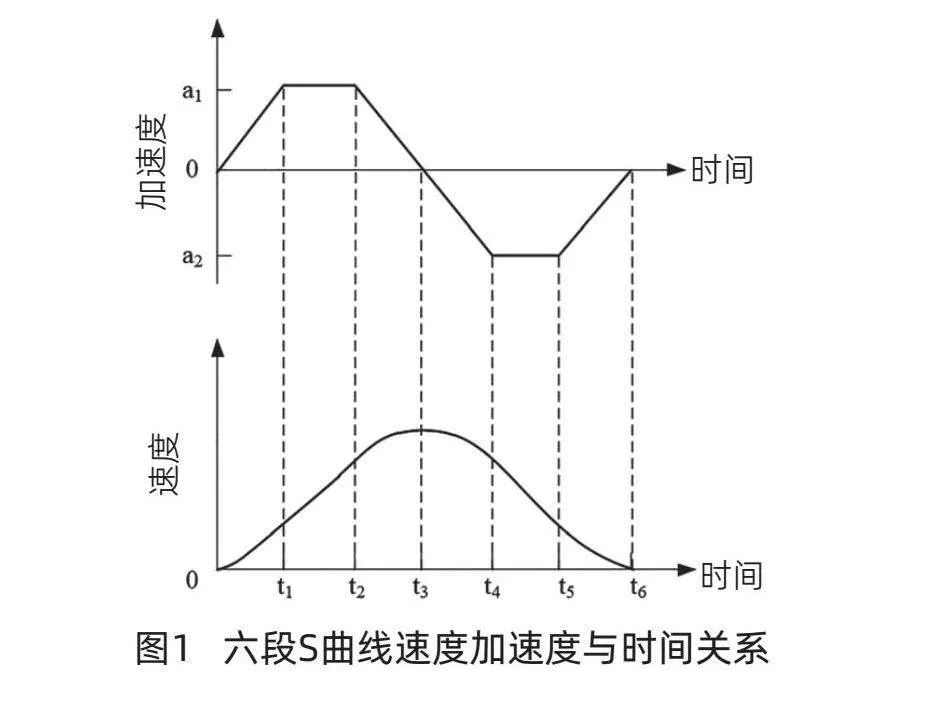
该模型描述了电动机速度、加速度和位置等随时间变化的关系。根据数学模型和特性，确定控制参数，如加速时间、匀速时间、减速时间、最大速度、最大加速度和最大减速度等[3]。将数学模型的控制参数输入控制器，控制器通常采用数字控制方式，通过计算机程序实现对电动机的精确控制。本文选用六段S曲线控制模型，其速度与加速度随时间的变化曲线，如图1所示。

从图1可以看出，六段S曲线数字阀步进电动机加减速控制是一种卓越的加减速模型。这种控制算法独特地分为6个阶段，它们分别是加加速段t1、匀加速段t2、减加速段t3、加减速段t4、匀减速段t5和减减速段t6。通过精细调整这些不同阶段的参数，可以获得各种性能卓越的加减速特性。

当t1≠0、t2=0时，S曲线将转变为三角形曲线，此时步进电动机加减速的时间最长；当t1=0，且t2≠0时，步进电动机的升、降速度最快，但由于加速度的突然变化，使步进电动机在起动和停止过程中均有脉动现象。当t1≠0，且t2≠0时，S曲线的算法比较复杂，但是能够确保步进电动机具有很好的运动特性。

1.2 六段S曲线控制模型的建立过程

在步进电动机控制中，可以采用S型曲线控制，使得加减速过程更加平稳、柔性快速。为了达到控制的目的，必须对其进行一些离散化的拟合和优化。同时，还应考虑到在不同频率下输出的脉冲的连续性，否则会出现丢步现象。假设步进电动机的运动状态由速度（v）、加速度（α）和位置（p）等3个变量表示，速度（v）、加速度（α）随时间（t）的变化关系可以描述为下列公式：

v（t）=v0+αt （1）

式中：v（t）表示速度；v0表示初始速度。公式（1）中，加速度α可以由下列公式计算得出：

（2）

式中：α（t）表示时刻的加速度，α0表示加速阶段的加速度，α1表示匀速运动过程中的加速度，t0表示加加速阶段的开始时间，t1表示匀加速阶段的开始时间。位置的计算公式为：

p（t）=p0+v0t+0.5αt2 （3）

式中：p（t）表示在某一时刻时的位置；p0表示初始位置。当电动机进入匀速阶段时，速度保持不变，加速度为零，因此速度和位置的计算公式可以简化为下列公式：

v（t）=v1 （4）

p（t）=p1+v1t （5）

式中：v1表示匀速阶段速度；p1表示进入匀速阶段后的位置。

1.3 现有7段型S曲线数学模型分析

现有的7段型S曲线是一个广泛应用的数学模型，它通过将运动过程分为启动、匀加速、匀速、匀减速、减速、停止和反向启动等7个阶段，来实现对步进电动机的精确控制。当加速与减速时，位移的总和大于实际所需位移，匀速段就会出现在中间的某个位置[4]。

电动机在加速到最大速度后，会保持这个速度一段时间，直到完成所需的位移。此时电动机将从启动开始以最大速度运行，直到完成所需的位移，然后在减速阶段逐渐降低速度直至停止。

根据上述对数字阀步进电动机运行时运行特性的分析，在本文研究中，用变量实现对变加速阶段变加速度的描述，其表达式为：

（6）

式中：h（t）表示某一时刻时的变加速度；hmax表示最大变加速度。

通过以上步骤，可以建立基于S曲线的控制模型，并将其应用于步进电动机的加减速控制中。该模型能够实现平稳地启动和停止，降低步进电动机的振动，延长其使用寿命、提高其控制精度[5]。同时，该模型还具有较好的适应性和可扩展性，能够适应不同的施工环境和负载条件。

确定控制目标是建立基于S曲线的控制模型的首要任务。在这个过程中，需要明确控制对象、控制精度和控制范围等关键要素[6]。

2 步进电动机加减速阶段与匀速阶段控制方法

2.1 步进电动机加减速阶段控制方法

结合S曲线的特性可以得出，加加速相位与减加速相位是对称的，加速过程中加速度能获得最大加速度这一条件是必须的。因而，当给定速度和初速之差不超过加速度的平方与最大加速度之比时，才会出现匀加速。进一步分析得出加速过程中加加速阶段的时间、匀加速阶段时间和减加速阶段时间，其表达式如下：

（7）

式中：t2表示减加速运行的开始时间；αmax表示最大加速度；vs表示最终速度。

根据目标速度和系统频率，确定加加速时间和减加速时间。若待测转速超过了系统的临界起动频率，则需经历一段加速→定速→降速→低定速→停机的过程。启动转速不能由零起步，而是要与起动转速相等或稍低于起动转速；在减速过程的末尾，转速通常应该与起动转速相等。

在加速阶段，根据设定的加速时间和起始速度，通过计算得到每一步需要达到的速度。在减速阶段，根据设定的减速时间和结束速度，通过计算得到每一步需要减小的速度。将加速阶段和减速阶段每一步的速度存放进一个数组，即可得到整个S型加减速的速度表。

2.2 步进电动机匀速阶段控制方法

电动机转速的调节是由电动机的加载相、加载脉冲频率来完成的。根据目标速度和系统性能确定电动机的通电相数。如果目标速度较低，可以减少通电相数以降低电动机力矩和转速；如果目标速度较高，可以增加通电相数以增加电动机力矩和转速。

根据目标速度和系统性能确定脉冲频率，脉冲频率越高，电动机转速越高；脉冲频率越低，电动机转速越低。在匀速阶段，根据设定的通电相数和脉冲频率，通过控制器实现对电动机的控制。控制器通常为一个微处理器或一个专门的控制器芯片，通过编程或设置来实现对电动机匀速阶段的控制。

在本文研究中，定义电动机在加速运行阶段时产生的位移为SAcc；定义减速运行阶段时产生的位移为SDcc；定义匀速运行阶段时产生的位移为s。若SAcc与SDcc之和小于s，说明曲线当中存在匀速运行阶段；若SAcc与SDcc之和大于或等于s，这就意味着曲线中并没有一个平稳运行的阶段，此时电动机实际最大速度与初始情况不同，需要重新计算速度最大值。

在匀速阶段，需要注意保持电动机的转速稳定，防止负载变化对电动机均速运行造成影响。若出现负载过大问题，需要及时调整通电相数和脉冲频率，以保持电动机的均速、稳定运行。

3 对比实验

3.1 实验方法

基于以上论述，本文提出的一种全新基于S曲线的数字阀步进电动机转速控制方法作为实验组。将基于FPGA（可编程逻辑电路）控制方法作为对照A组，将基于STM32（微控制器）控制方法作为对照B组，进行对比实验。该实验选用型号为SST59D5105数字阀步进电动机，该型电动机的基本性能参数如表1所示。

在实验中，为了公平比较两种控制方法的效果，首先设定了相同的目标速度。这个目标速度是根据实际施工需求和电动机性能来设定的，旨在模拟实际施工场景中的速度要求。

3.2 实验结果

按照上述方法对3个实验组进行了实验，根据电动机的当前速度和目标速度计算出合适的加速度和减速度，通过数字阀控制电动机的脉冲输入来实现平稳的启动和停止。实验过程中，记录电动机的速度变化、加速度和减速度等数据，以便后续结合数据进行分析，如表2所示。

通过分析可知，实验组控制方法的最大加速度和最大减速度相对较小，说明该方法能够更平稳地控制电动机的速度变化，减少冲击和振动问题。该方法能够更加精确地控制电动机的速度变化，减少冲击和振动问题，提高施工的精度和效率。该方法还具有更好的适应性和可扩展性，能够适应不同的施工环境和负载条件。

综上所述，基于S曲线的数字阀步进电动机加减速控制方法在工程施工领域具有广泛的应用前景，值得进一步推广和应用。

4 结束语

本文提出的基于S曲线的数字阀步进电动机加减速控制方法，通过精确控制步进电动机的启动、运行和停止过程，提高了控制的稳定性和精度，延长了步进电动机的使用寿命。该方法简单易行，适用于各种类型的步进电动机，为实现步进电动机的智能化控制提供了有效途径。基于S曲线的数字阀步进电动机加减速控制方法在工程施工领域具有广泛的应用前景，值得进一步推广和应用。

参考文献

[1] 习晓飞，汪旭东，孙彦，等.微型永磁式爪极步进电动机控制系统设计与实现[J].微电动机，2023，56（4）：63-67+72.

[2] 王庆，周锋，郭乃宏，等.基于FPGA的裁切机步进电动机控制算法设计[J].计算机测量与控制，2022，30（11）：127-132+160.

[3] 丛峰武，高太，李熙然，等.基于模糊PID的轨道式巡检机器人步进电动机控制算法[J].数字技术与应用，2022，40（11）：21-24.

[4] 杨鉴.基于AT89C52单片机的两坐标步进电动机控制系统 设计[J].湖南工业职业技术学院学报，2021，21（4）：17-19+39.

[5] 闫吉.基于STM32的3D打印步进电动机控制方法研究[J].制造业自动化，2021，43（11）：129-131+136.

[6] 唐钏，刘昱，曾林.面向步进电动机控制的RISC-V微控制器的设计与实现[J].重庆大学学报，2021，44（11）：31-39.