跨铁公路转体桥墩中转体系统受力分析

摘要：以墩中转体施工桥为研究对象，通过建立数值分析模型，对墩中转体球铰在竖向荷载作用下的受力状况进行分析。采取数值模拟的方法，对球铰的应力分布、变形以及球铰与墩身之间的相互作用进行详细分析。研究结果表明：在竖向荷载作用下，球铰的应力分布呈现出明显的非线性特征，且随着荷载的增加，球铰的变形逐渐增大。球铰与墩身之间的相互作用也表现出一定的非线性特征，对球铰的受力状况产生一定影响。所述研究方法和研究结果，可以类似工程墩中转体球铰的设计和优化提供重要的理论依据。

关键词：高墩；墩中转体；墩中转体球铰

0 引言

桥梁转体施工法是桥梁结构的主要施工方法之一，既可降低桥梁建造对既有线路运营的影响，也可以在特殊地区使用。近年来，许多专家学者针对桥梁转体系统受力性能开展相关研究。李慧萍[1]等人深入探讨了城市环境下桥梁转体施工的技术难点及解决方案，对于在复杂城市环境中应用转体施工技术有着重要的指导意义。李彪[2]等人对桥梁转体施工法在现代基础设施项目中的高效性进行了细致分析，指出其在缩短工期、降低成本上的显著优势。刘芳[3]等人提出了一种新型的基于模块化设计的预制转体桥梁构件，为提高施工效率和施工质量提供了可能。苏晓堃[4]等人研究了多个案例分析，展示了转体施工技术在不同类型桥梁中的应用，及其在解决特定施工挑战方面的效果。

本文以墩中转体施工桥为研究对象，建立数值分析模型，在竖直荷载的影响下，分析桥墩中的转体球铰的力学表现。

1 工程概况

本工程为107北互通式立交主线上跨京广铁路，京广下行线与道路轴线交点里程铁路里程为K368+726.86（公路里程为K10+421.31），交角为85.7°。交叉处既有上行线铁路轨顶高程为72.96m，下行线铁路轨顶高程为72.76m。

本工程段公路跨越既有京广铁路处于半径2000m曲线段，与公路的相交角度为85.7°，在跨越铁路的主孔外引桥范围位于圆曲线及缓和曲线上。上跨方案桥位处于1.8%及-3%坡段上。本工程跨京广铁路段设计范围内，桥梁孔跨布置为（4×30）m+2-（3×30）m先简支后连续预应力混凝土小箱梁+2×55m T构桥。其中2×55m的T型刚构桥为跨铁路联，采用转体施工。

本桥施工范围为主桥与引桥桩基、承台、墩柱、转体现浇梁及相关附属设施。主桥上部结构采用（2×55）m变截面预应力混凝土T构跨越京广铁路，转体施工。转体部分跨径组合为（50+50）m，上部结构整幅设计，主墩采用双肢薄壁墩，桥面全宽34.5m，转体质量14200t（包括护栏、防护屏）。

桥梁荷载标准为公路Ⅰ级，铁路孔提高30%。道路等级为一级公路，设计时速80km/h。结构设计基准期100年。本工程为重要结构，安全等级为一级。跨铁路联桥梁标准横断面为双向6车道，0.5m防撞墙+15.5m行车道+0.5m防撞墙+1.5m中央分隔带+0.5m防撞墙+15.5m行车道+0.5m防撞墙，桥面宽34.5m。路面横坡超高2%。跨京广铁路净高≥8.3m。

2 数值分析模型

以墩高40m的6号墩为研究对象，转体系统布置在高31m的墩中部。转体系统由上转盘、下转盘、转动牵引系统、转动支撑系统、防倾覆装置、限位装置等组成。上转盘设置转动牵引系统，下转盘设置转动支撑系统和防倾覆装置，限位装置设置在上转盘和下转盘。

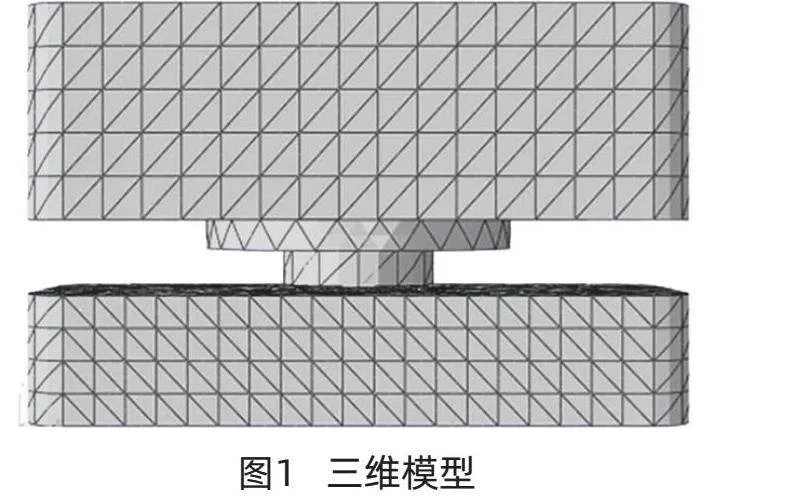
模型上墩身长度为70m，宽度为20m，高度为20m，下墩身长度为70m，宽度为20m，高度为18m。上转盘直径为30m，下转盘直径为15m。三维模型如图1所示。

3 结果分析

3.1 不同中心距离下球铰接触面竖向应力

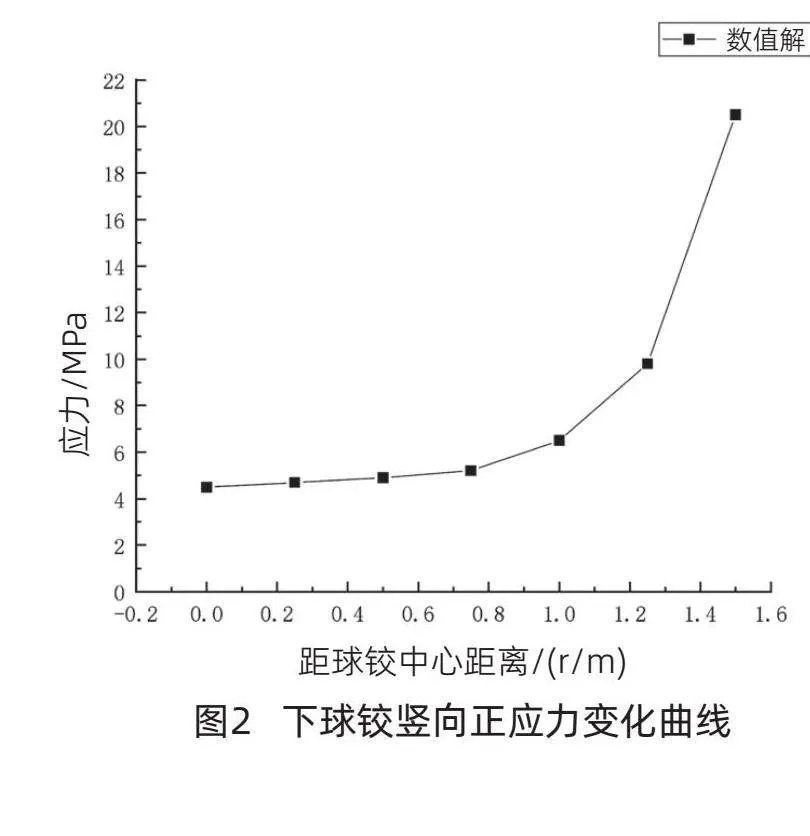
基于上述模型，分析墩中转体系统在竖向荷载影响下的受力情况。不同球铰中心距离下球铰接触面竖向应力值如表1所示。竖向应力随球铰中心距离的变化曲线如图2所示。

从图2可以看出，在竖向荷载作用下，球铰系统的应力分布呈现出明显的非线性特征。随着距球铰中心距离的增加，下球铰所受到的应力逐渐增大，但增大的速率并不是均匀的。在距球铰中心距离1.25～1.5m的范围内，下球铰的应力从9.8MPa突变到20.5MPa。

这种突变现象表明在该部位应力受到了较大的集中作用。为此在设计中要考虑增强结构，以减小这种应力集中的影响。在结构设计和分析时，确保应力分布的均匀性是至关重要的，因为不均匀的应力分布会导致局部过度负荷，进而可能造成材料的疲劳损伤甚至是结构性损坏。

3.2 不同圆心角上球铰正应力变化

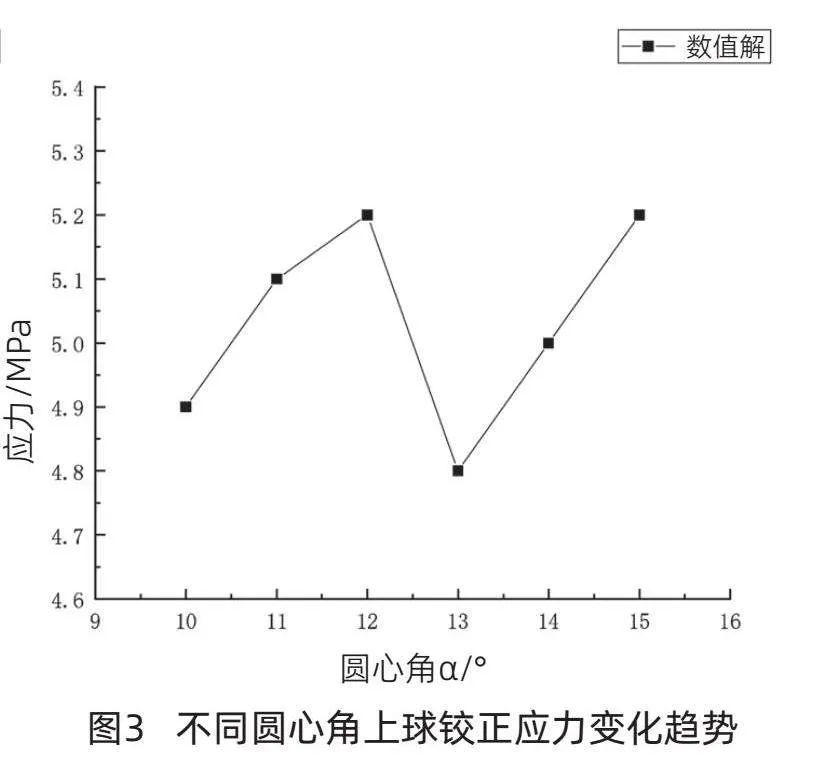
为分析不同圆心角上球铰下墩中转体结构中对上球铰应力影响，建立6种不同圆心角模型：10°、11°、12°、13°、14°15°。不同圆心角上球铰正应力变化趋势如图3所示。

从图3中可以看出，随着圆心角的增大，上球铰竖向正应力呈现先增大后减小再增大的趋势。在圆心角10～12°时，上球铰竖向正应力逐渐增大，并在12°时达到最大值。这由于在这个角度范围内，上球铰受到的压力逐渐增大，导致正应力也随之增大。

然而，当圆心角继续增大到13°时，上球铰竖向正应力突然下降到最小值。这是由于在这个角度下，上球铰受到的压力突然减小导致正应力减小。当圆心角继续增大到15°时，上球铰所受到的正应力达到5.2MPa。

从图3还可以看出，在圆心角12～13°之间，上球铰竖向正应力变化幅度较大，说明在这个角度范围内，上球铰受到的压力变化较为明显。

3.3 不同圆心角对应下球铰承台竖向正应力

为分析不同圆心角承台在荷载作用，下墩中转体结构中对下球铰应力影响，对不同圆心角进行了数值模拟分析。不同圆心角对应下球铰承台竖向正应力如图4所示。

由图4可知，当圆心角为10°时，下球铰承台的正应力达到最大值17.3MPa。这表明在这个角度下，承台受到了最大的扭矩作用，导致正应力达到最大。随着圆心角的逐渐增大，承台所承受的扭矩逐渐减小，因此正应力也呈现出逐渐减小的趋势。当圆心角为15°时，下球铰承台的正应力达到最小值7.3MPa。这表明在这个角度下，承台所承受的扭矩最小，导致正应力也最小。

综上所述，下球铰承台的正应力与圆心角之间存在线性关系，随着圆心角的增大，承台的正应力逐渐减小。这种变化趋势是由于随着圆心角的增大，承台所承受的扭矩逐渐减小，从而使得正应力也随之减小。

3.4 不同圆心角对应下球铰外缘正应力

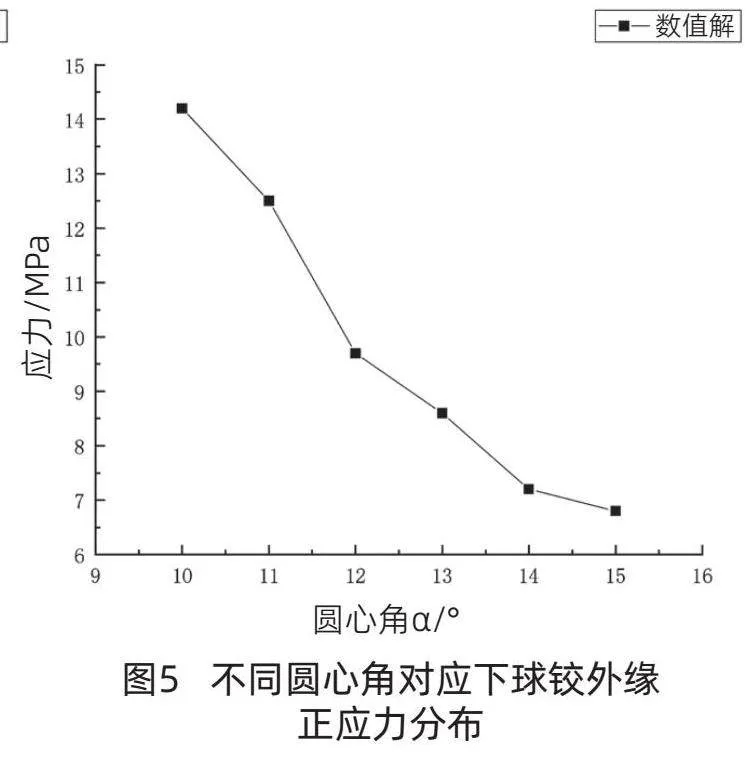
为分析不同圆心角下球铰在荷载作用下墩中转体结构中对下球铰应力影响，对不同圆心角进行了数值模拟。不同圆心角对应下球铰外缘正应力如图5所示。

从图5中可以看出，随着圆心角的增大，下球铰外缘的竖向正应力呈现出先增大后减小的趋势。这主要是因为在圆心角较小时，球铰所受到的压力较大，导致其外缘竖向正应力较大。而随着圆心角的增大，球铰所受到的压力逐渐减小，从而使得其外缘竖向正应力逐渐减小。

当在圆心角为10°时，下球铰外缘的竖向正应力达到最大值14.2MPa。而在圆心角为15°时，其竖向正应力最小，为6.8MPa。这说明在圆心角逐渐增大的过程中，球铰所受到的压力逐渐减小，从而使得其外缘竖向正应力逐渐减小。

进一步分析可得，下球铰外缘的竖向正应力分布，随着圆心角的增大而呈现出一种非线性的变化趋势。在圆心角较小时，应力分布较为均匀，随着圆心角的逐渐增大，应力分布逐渐向球铰的中心区域集中。这是因为在圆心角增大的过程中，球铰所受到的压力逐渐减小，而其外缘的曲率半径逐渐增大，导致应力集中程度增加。

3.5 不同摩擦系数下球铰应力

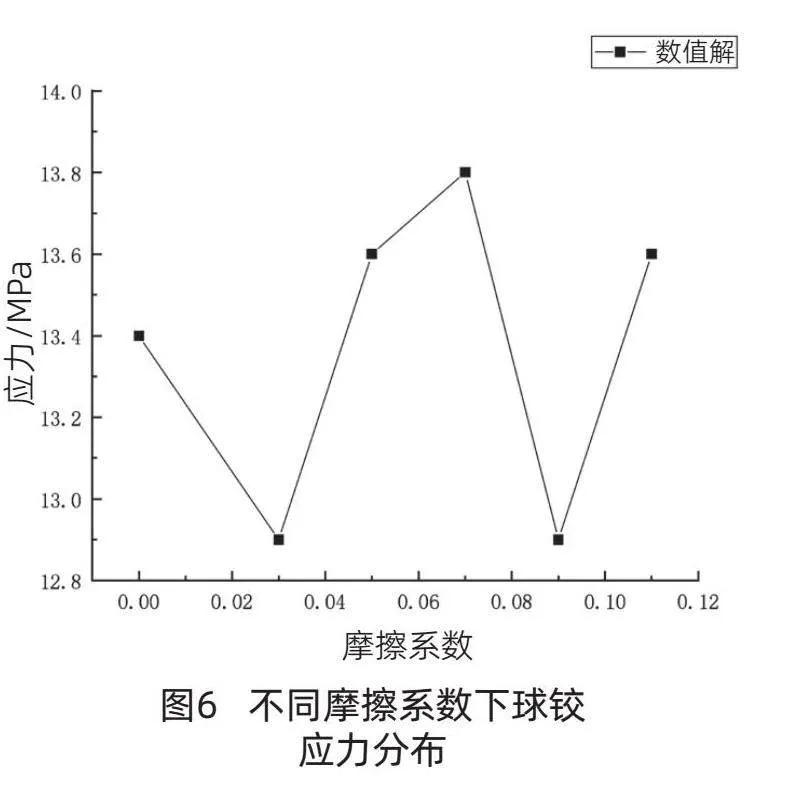
选取0、0.03、0.05、0.07、0.09、0.11等6组静摩擦系数来探究对下球铰应力值的影响。不同摩擦系数下球铰应力如图6所示。

从图6中可以看出，摩擦系数和应力值的变化并不是简单的线性关系。在摩擦系数从0～0.03的过程中，应力值从13.4MPa下降到12.9MPa，这表明在这个阶段，摩擦系数的增加对系统的影响是负面的，导致应力值下降。然而，当摩擦系数从0.03增加到0.07时，应力值却呈现增大的趋势，这表明在这个阶段，摩擦系数的增加对系统的影响是正面的，导致应力值增大。

当摩擦系数从0.07增加到0.09时，应力值又呈现减小的趋势。这表明在这个阶段，摩擦系数的增加对系统的影响是负面的，导致应力值下降。分析认为，因为在这个阶段，摩擦系数的增加超过了系统的承受能力，导致应力值下降。

在摩擦系数为0.07时，应力值达到最大，为13.8MPa。这表明在这个点上，摩擦系数与系统之间的相互作用达到了一个平衡状态，导致应力值达到最大。而在摩擦系数为0.09时，应力值达到最小，为12.9MPa。这表明在这个点上，摩擦系数对系统的影响较小，导致应力值达到最小。

4 结束语

本研究以墩中转体施工桥为研究对象，通过建立数值分析模型，分析在受竖直荷载作用时分析转体球铰的力学特性。研究球铰的应力分布和变形情况，分析其与桥墩接合部位的相互作用和影响，得出以下结论：

在竖向荷载作用下，球铰系统的应力分布呈现出明显的非线性特征。随着距球铰中心距离的增加，下球铰所受到的应力逐渐增大，但增大的速率并不是均匀的。

随着圆心角的增大，上球铰竖向正应力呈现先增大后减小再增大的趋势。在圆心角10～12°之间，上球铰竖向正应力逐渐增大，并在12°时达到最大值。

下球铰承台的正应力与圆心角之间存在线性关系，随着圆心角的增大，承台的正应力逐渐减小。

参考文献

[1] 李慧萍.桥梁转体的施工方法及应用分析[A].《建筑科技与管理》组委会.2013年2月建筑科技与管理学术交流会论文集[C].《建筑科技与管理》组委会，2013（2）：61-62.

[2] 李彪，郭攀.高墩连续刚构桥0号块托架预应力方案可行性研究[J].公路工程，2016，41（2）：260-264.

[3] 刘芳.我国桥梁转体施工技术的发展现状与前景[J].科技视界，2014（3）：106-107

[4] 苏晓堃.公路铁路桥主桥双福同步平衡转体施工技术研究[J].科技创新导报，2012（11）：112-113.