有限元分析技术在起重机升级改造中的应用

摘要：起重机结构复杂，通过传统方法进行升级改造需要大量的人员进行操作和调试，以至于能耗过高，为了解决这个问题，提出了有限元分析技术在起重机升级改造中的应用。通过模型简化分析，建立起重机结构有限元模型，计算出起重机相关技术参数，并对主梁下挠结构进行优化，进而将有限元分析技术应用在起重机升级改造中。采用对比试验进行验证，研究结果表明：该方法在对起重机升级改造方面有显著效果，可以有效地降低能耗，提高设计质量和安全性。

关键词：起重机；有限元分析；升级改造；能耗

0 引言

起重机作为重要的工业设备，在物流和生产领域中发挥着重要作用。但是，随着时间的推移和使用环境的恶化，起重机往往会出现性能下降、结构疲劳和安全隐患等问题，因此必须对其进行升级改造[1]。

有限元分析技术作为一种现代化的工程分析方法，被广泛应用于结构设计优化和性能评估。在对起重机进行技术改造时，可以将有限元分析技术应用于起重机结构优化设计，提高起重机的承载能力和运行稳定性，减少结构疲劳和振动问题。同时，也可将其用于评估和验证新设计的性能，包括起重能力、精度、速度和能耗等方面，从而确保改造后的起重机满足现代生产需求。

有限元分析技术在起重机升级改造中的应用具有重要意义，其不仅可以提供可靠的结构设计依据和性能评估，减少升级改造过程中的试错成本，还能够确保起重机达到更高的安全标准，提高工作效率，推动起重机行业的发展和进步[2]。

1 起重机升级改造方案设计

1.1 建立有限元模型

1.1.1 模型简化

为了使模型更加合理，有必要对其进行必要的简化。由于起重机的回转结构和其他固体零件尺寸较小、刚度较大且质量集中，因此在起重机结构整体分析时，可以对回转结构和其他固体构件进行等效处理，以减小构件类型，便于后期处理。通过对整个结构进行分析，计算出等效构件的结点力即为外部荷载，然后重新对旋转结构进行分析。

起重机的附属装置因其几何尺寸小且质量集中，与起重机的整体结构相比，可以在分析整个结构时对其进行等效处理。变幅式钢索分布较为均匀，在模型中可以通过调整对应杆件的密度，使其具有一定的质量来考虑其影响[3]。

1.1.2 建立模型

起重机属于空间结构，因此采用有限元法对其进行有限元分析。在起重机中，每个节点都有6个自由度：3个是沿x、y、z方向的平动，3个是绕x、y、z轴的转动。考虑到起重机的结构特征，将塔架、平衡臂及吊杆的主要杆件都作为梁单元来处理，并选取Beam188单元，以便于计算。

利用空间桁架单元Link8模拟悬臂及平衡绳的受力情况，该单元具有2个节点，每个节点3个自由度，DN1PVwM6cXIrPb8+hPLsCTHGtL2QQL3ceTpip/WxWYU=只承受轴向力。不考虑杆件的弯曲、扭转等因素，采用有限元法模拟2点、3自由度的空间杆系。

回转工作台为板壳结构，回转支座为三维固态结构，相对于起重机整体结构，其几何尺寸非常小，但其刚度和质量都比较大，因此在对起重机结构进行整体计算时，可以将转动支承等效为梁元，这样就克服了2个不同自由度所带来的连接难度。

该单元为6个自由度的粒子单元，能较好地反应被测体在空间的分布。在此基础上，以配重、起升、变幅等为重心质量，采用3D-MASS21质点模型，对其进行求解。

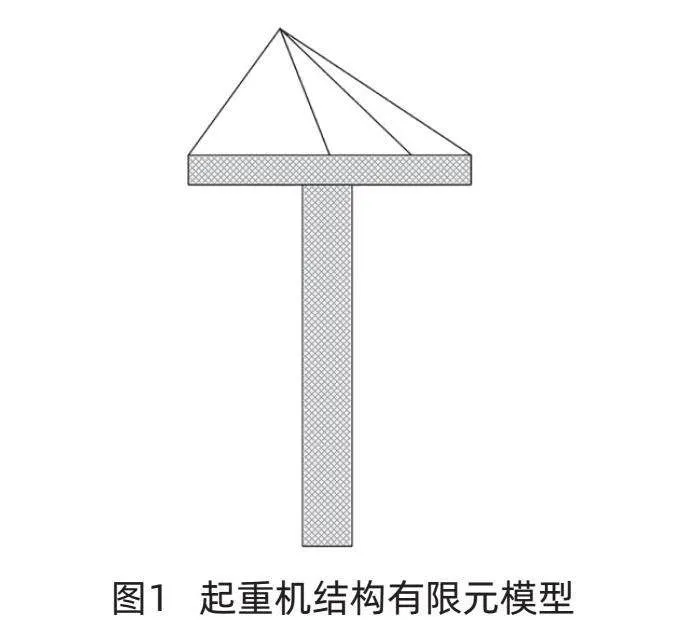
综上所述，根据设计要求，建立多梁、3杆、10个MASS21单元的起重机结构有限元模型。该模型以节点为单位，采用直接和间接方法建立。起重机结构有限元模型如图1所示。

1.2 计算起重机技术参数

根据起重机结构有限元模型，计算起重机相关技术参数[4]。

1.2.1 吊装荷载

吊装荷载是指起重机能够安全吊装的最大货物重量。通过起重机结构有限元模型计算不同工况下的吊装荷载，其公式如下所示：

N=φ1（φ2Q+q） （1）

式中：φ1表示载荷；φ2表示超载系数；Q表示主钩起吊负荷；q表示小车及吊钩质量。

1.2.2 静挠度

静挠度是衡量起重机在静力荷载作用下的变形能力的指标。通过起重机结构有限元模型计算起重机的静挠度，其公式如下所示：

（2）

式中：φ1表示载荷；l表示起重机两支撑点之间的距离；E表示弹性模量；I表示截面惯性矩。

1.2.3 最大应力

最大应力是起重机在各种工况下各部件承受的最大应力。通过起重机结构有限元模型计算起重机的最大应力，其公式如下所示：

（3）

式中：m表示平均应力；r表示应力比；I表示截面惯性矩。

1.2.4 刚度

刚度是衡量起重机结构抵抗变形能力的指标。通过起重机结构有限元模型计算起重机的刚度，其公式如下所示：

（4）

式中：M表示起重机负载和自身结构的质量；g表示重力加速度；x表示起重机在满载条件下产生的最大挠度。

1.2.5 频率与振型

通过起重机结构有限元模型，可以计算起重机的固有频率和振型。这些参数反映了起重机对外部激励的响应能力。频率计算公式如下所示：

（5）

式中：K表示刚度矩阵；M表示起重机负载和自身结构的质量。

振型公式如下所示：

R=（K-2M）-1H （6）

式中：K表示刚度矩阵；M表示起重机负载和自身结构的质量；H表示力向量。振型向量描述了结构在不同频率下的振动形状。

综上所述，利用起重机结构有限元模型，得出起重机吊装荷载、静挠度、最大应力、刚度、频率、振型等技术参数[5]。

1.3 主梁下挠结构优化

1.3.1 确定优化方案

起重机主梁大都为箱型结构，箱形结构紧凑但易变形，容易发生下挠现象，从而导致大车啃轨、小车爬坡滑车、电机过载等问题，严重时还会发生重大的设备和人员事故。根据起重机技术参数，对起重机主梁下挠结构进行优化，分为支撑、调火、拉筋张拉、焊补4道工序进行[6]。

1.3.2 具体步骤

具体步骤如下：

一是在梁底1/4、1/2、3/4部位各设3个测点，每一测点采用200mm厚壁钢管支承，在1/2位的钢管下端设置100t千斤顶，以保证炉温加热时可以顶动梁的上拱。

二是对主梁两端各1/5的位置进行了修正，使得其易于变形，从而易于实现矫形。

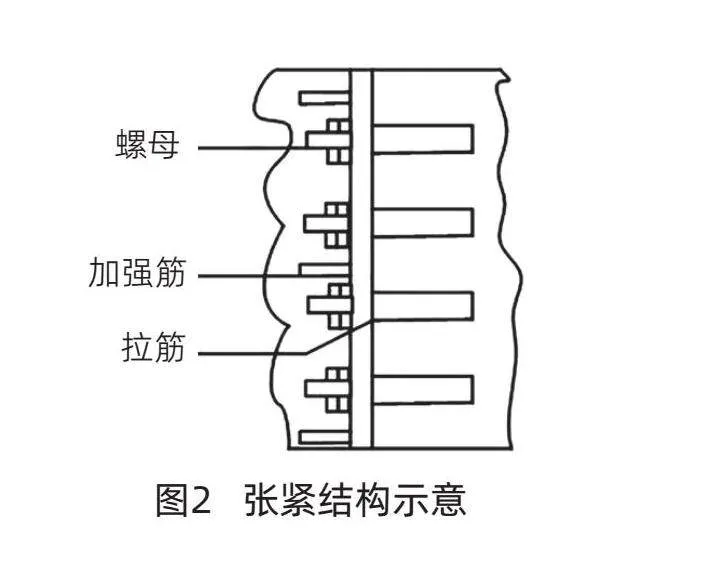
三是在梁底下盖板两端距离梁端部3m左右的位置，设置2个支撑座，各设4个孔，采用20mm圆钢作为拉伸筋，拉筋上的螺帽转动，与千斤顶共同工作，从而形成上拱。张紧结构示意如图2所示。

四是待拱度满足要求后，将10mm厚的钢板覆盖在被烘焙的钢板上。如此不是为了增强起重机桥架的强度和刚度，而是为了增强此处的钢板。由于钢板内会形成内应力，为此存在导致主梁再次下挠的因素[7]。

2 试验论证分析

为了验证有限元分析技术在起重机升级改造中的有效性，设计对比试验。

2.1 试验准备

采用能耗测试仪器测量起重机的能耗，验证有限元分析技术在起重机升级改造中的应用是否能够降低能耗。还需要准备一台计算机，用于有限元分析技术在起重机升级改造的模拟计算，具体硬件和软件配置如表1所示。

根据上述内容，选择具有代表性的两种传统方法升级的起重机和采用有限元分析技术升级改造的起重机作为试验设备。在试验中，设置同样的试验环境和参数，以确保试验的准确性和可比较性。

2.2 试验结果分析

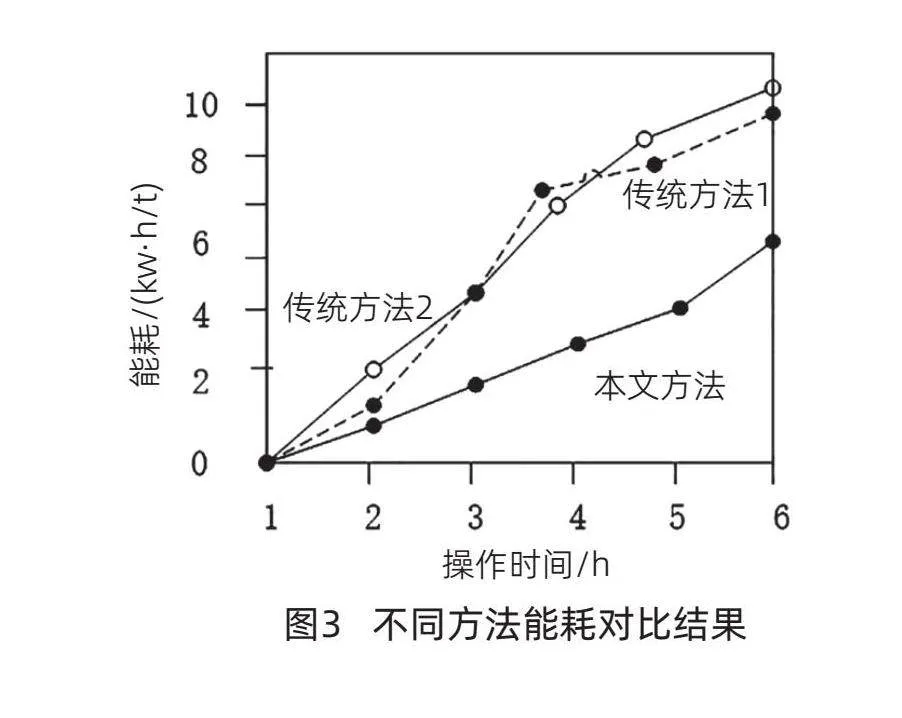
根据上述试验准备进行试验，得到不同方法能耗对比结果如图3所示。通过图3的对比结果，可以清晰地展现出3种方法的能耗表现。随着操作时间逐渐增加，本文方法的能耗始终低于传统方法1和传统方法2的能耗。特别值得注意的是，本文方法的能耗最高达到6kW·h/t左右，整体能耗保持在一个相对较低的水平。相比之下，传统方法1和传统方法2的能耗高达到10kW·h/t左右。这种能耗水平的差异使得限元分析技术在起重机升级改造方法在可行性上具有显著的优势。

综上分析，采用本文方法对起重机进行升级改造，可以有效地降低能耗，提高设计质量和安全性。即使在长时间操作的情况下，也能够保持较低的能耗水平，从而确保了起重机的稳定性和高效性。

3 结束语

在起重机的升级改造过程中，有限元分析技术发挥着重要的作用。通过对起重机进行有限元分析，可以获取其在不同工况下的应力、应变、位移等重要参数，为优化设计提供了科学依据。有限元分析技术能够将起重机整体划分为多个小单元，通过计算机模拟起重机的实际工作状态，从而得到更精确的分析结果。这有助于减少传统试验方法的成本和时间，提高设计效率。

有限元分析技术的应用也存在一定的局限性。由于模型的简化和边界条件的设定，对计算结果的精度有很大的影响。所以，在进行有限元法分析时，必须与实测资料相结合，加以比较和检验，以确保分析结果的可靠性。

综上所述，有限元分析技术在起重机的升级改造中具有广泛的应用前景。通过引入有限元分析技术，可以大大提高起重机的设计质量和安全性，为设备优化提供有力支持。

参考文献

[1] 牛春江，马兵书，郑红旭，等.炼钢厂抓斗式桥式起重机改造设计与应用[J].山东冶金，2023，45（3）：77-78.

[2] 郑勇.岸边集装箱起重机自行式小车牵引式改造设计方案[J].工程建设与设计，2022（10）：104-106.

[3] 邹石桥，喻颖，谌晓波，等.起重机改造重大修理术语定义变化的思考分析[J].中国设备工程，2021（23）：9-10.

[4] 李忠良，张国良，陈生.桥式起重机变频改造与无线遥控设计[J].福建冶金，2021，50（2）：45-47+44.

[5] 张荣军，王俊君.FZQ-2000Ⅱ型电站塔式起重机升级改造分析[J].中国电力企业管理，2021（3）：90-91.

[6] 郭富强，宋贺.420t电站起重机与厂房干涉原因论证与改造[J].设备管理与维修，2020（15）：80-81.

[7] 王玉泽，徐巍，张福江，等.基于既有建筑单元式幕墙改造的塔式起重机施工部署研究与应用[J].施工技术，2020，49（2）：45-48.