素养导向的学科实践：思维可视化的实现路径

[摘要] 20多年的数学课程改革，“满堂灌”的课堂形态得到较大改变，但虚假探究现象仍较突出。新课改要求学生以实践的方式进行学科学习，展现思维的过程与结果，让“探究”迭代升级。数学学科实践是实现思维可视化的路径之一，思维可视化助力数学学科实践育人价值的彰显。基于对课标、教材、学情的准确把握，多样实践形式让思维“看得见”“看得清”“看得远”。围绕问题解决，以问题解决为导向，构建真实有意义的情境，激活学生认知及探究的心理，引导学生经历问题表征、策略探究、方法迁移、模型构建等可视化过程，发展数学思维素养。数学学科实践并不是数学学习的唯一方式，应根据学习内容与学习对象特点灵活选择多种学习方式，合理进行思维可视化，发展学生核心素养，实现学科育人功能。

[关键词] 核心素养；学科实践；实践育人；思维可视化；数学学科特质

[中图分类号] G64[文献标识码] A[文章编号] 1005-4634（2024）05-0086-07

数学课程改革已实施了20多年，课改突出综合实践活动的“实践”功能，“自主、合作、探究”学习方式的普遍运用，使“满堂灌”的课堂形态得到较大改变。但是，数学学科实践基本上还是项目式学习或主题活动形式，“为探究而探究”的“虚”“假”“泛”“浅”“僵”现象仍较突出，无法从根本上促进学生“像专家一样思考与行动”、用“学科的方法”获得并实践“学科知识”，实现知行合一和自我建构。2022年，《义务教育课程方案和课程标准（2022年版）》正式实施，要求将“实践”融入到各学科课程学习中，促使“自主、合作、探究”迭代升级，以实践的方式进行学科学习，展现思维的过程与结果，提升学生思维能力与动手操作能力，将学科实践转化为学科素养。

从学科特性出发，以学科独有的方式学习，以学科实践落实学科育人，培育学生综合素养，是学科实践的出发点与归宿。数学学科实践离不开思维参与，以独特的思维方式解决数学问题，使数学知识转向数学素养发展。“鸡兔同笼”是经典的数学问题，多种版本教材均安排了此内容。人教版安排在四年级下册“数学广角”探究活动中，主要目的是让学生经历自主探索问题的解决过程，呈现思维历程，理解列表、画图、假设法，在学科实践中渗透数学思想与方法，发展学生数学核心素养。下面以“鸡兔同笼”教学为例，探讨如何在学科实践中发展学生思维能力。

1数学学科实践、思维可视化的逻辑关系

1.1数学学科实践的内涵

20世纪50年代，施瓦布（iCBfuST5sZc2ga3Aosv9VQ==Schwab J J）在亚里士多德、杜威等人思想的基础上提出并发展了实践课程概念，认为实践课程具有“真实性、探究性、过程性与情境性”等特点[1]，驱动着对学科实践内涵的重构。“学科实践”是针对真实情境中的特定问题，运用具有学科特点的做法，让学生像专家一样，通过动手和动脑亲身体验探究的过程[2]。传统的学习方式多为记忆、练习、理解、思考等，本次课程改革，将从根本上改变传统的“坐而论道”等育人方式，强化行动、体验、感悟、思维、创造等多样学习形态。杜威的名言“教之于学犹如卖之于买”，阐明了将书本知识转化为学生的知识的重要性。只有亲身经历知识产生的历程，让知识在“基于实践、通过实践、为了实践”的过程中产生、应用与发展，才能使“学了”变成“学会了”，才可能将书本知识变为学生的知识。学科实践不仅可以使学生学习和运用新知识，而且能促进其综合素质的发展[3]。

数学学科实践是以数学学科知识学习为基础，以真实问题情境和高阶思维参与为基本特征，围绕数学问题解决，以发展学生数学眼光、数学思维、数学语言为目的的实践学习方式，也是一种对知识的理解、探究和创造的数学学习活动。数学学科实践样式包括但不仅限于综合与实践活动课程，一般包括以探索发现为目标的数学问题探究、以验证理解为目标的数学实验操作、以综合应用为目标的主题活动或项目活动3种基本样式。数学探究性学习从本质上说是一种数学学科实践形式。加拿大不列颠哥伦比亚省课程改革，设置了各个学科的实践方式，其中数学实践包括“推理和分析”（reasoning and analyzing）、“理解和解决”（understanding and solving）、“沟通和表征”（communicating and representing）、“联系和反思”（connecting and reflecting）。“鸡兔同笼”问题，具有较强的探究性，让学生亲身经历“假设—比较—调整”的问题解决的过程，能够积累数学经验，训练思维能力，发展数学运算、逻辑推理、直观想象、数学建模等核心素养。

1.2思维可视化的内涵

思维可视化，是“让思维可见”，以恰当的操作活动（如直观语言、图式表征、动作操作等），将“看不见，摸不着”的思维，变得“看得见，摸得着”，让他人能看得见自己的思考路径，让自己看得见思维的影响，从而促进思维成长。约翰·哈蒂提出了 “可见的学习”核心概念，当 “可见”发生时，对学生学习产生的效应最大[4]。 根据活动理论内化和外化结合的原则，学科实践活动有将学生个体的认知转化为外在行为的外化过程，改变着学生的学习方式。因而，学科实践活动是由内化转向外化，再由外化影响内化的过程。思维可视化，是小学数学深度学习的典型特征。借助思维外显手段，有利于将抽象的数学知识具象化，把内隐的思维过程外显化，实现“内”思考与“外”表现的转化，激发学生主动思考的意识与活力，实现真正的深度学习。“鸡兔同笼”课堂学习，借助简单的图形、表格等表征形式，记录了猜想的过程，留下了思考的痕迹，呈现多种列表方法，发展了学生思维的灵活性、独创性。

1.3数学学科实践与思维可视化的关系

1.3.1数学学科实践是实现思维可视化的路径之一

数学学科实践的本质要求是用数学独特的方式学习数学，是基于数学学科特点，体现数学学科思想和数学方法，彰显数学意蕴的学习方式。没有思维参与的实践不是数学实践。数学学科实践以问题探究为核心，思维过程与思维形式则是问题探究的内在逻辑和最终追求[5]60 。再现与描述思维过程和思维形式，即是思维可视化的过程。数学学科实践能引发学生数学思考，用数学的思维方式方法发现问题与解决问题，并形成清晰的数学逻辑思路，用恰当的形式将思考过程表现出来并与他人交流，实现了思维的可视化。“鸡兔同笼”教学将学生带入古今对同一问题解决方法的差异化情境中，引导学生用已有的知识与经验进行猜想、验证，经历列表有序思考—绘图数形结合—运算验证等实践操作过程，以列表、画图、算式等方式将思考过程可视化，实现了“学科实践”与“思维可视化”的巧妙结合，学生的知识体系得到了自主建构。

1.3.2思维可视化彰显数学学科实践育人价值

根据多维学习理论，借用数学符号、图形、文字语言或者动作等表达数学实践过程与结果，让学习过程外显、情境可视，学生必定能得到全新的心理体验，激发多种感官参与，促进“四基”“四能”发展，形成正确的情感、态度和价值观。

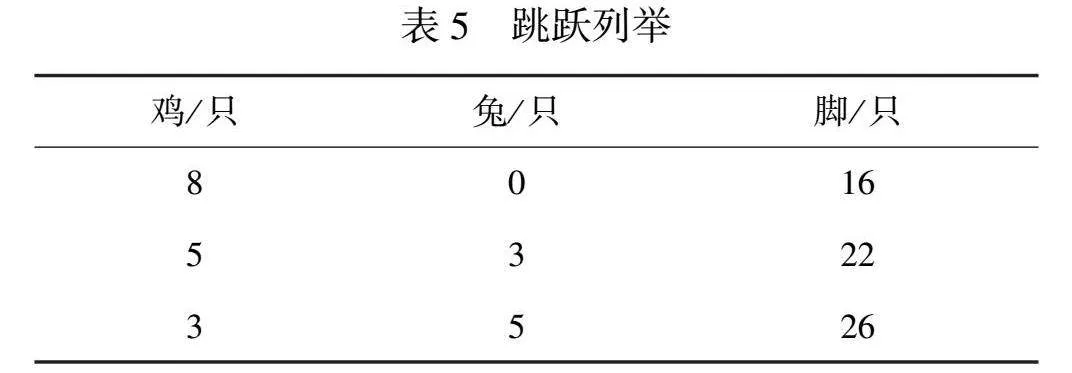
数学学科实践结果相同，并不等于思维过程一致。问题解决方法的多样性，取决于思维方式的多样性。学生在用列表法解决“从上面看有8个头，从下面数有26只脚，鸡兔各有几只”问题时，在得出“鸡3只、兔5只”正确答案的学生中，所用方法与时间统计见表1。

由此可见，学生虽都用列举方法得到了正确答案，但思维过程有异，用时也有较大差异。针对几种列举法，教师引导学生结合“添足”或“抬脚”画图法，进行对比分析，沟通了列举与假设法的关系，深刻理解了假设法的本质，进一步彰显了分享活动前学生自主探究实践活动的价值。

多样的思维可视化方式，优化了实践操作过程。“画出来”“写出来”“说出来”更能推进“做”得更好。在解决“鸡兔同笼”的问题时，教师请8位学生到台上扮演鸡和兔，尝试有26只脚在地，提出问题：“需要有几位学生扮演鸡或兔？”经过讨论，有5位学生自然将“手”扮为兔足。他们既能表演出装扮的过程，也能描述为什么这样装扮，“所说”即“所想”，以“说”的方式表达“想”和“做”的过程。当头不变（学生人数不变）时，探究如何调整“足”的数量，降低了实践操作难度，也优化了操作过程。

学科实践包含了多种思维可视化方式，正确应用能有效地促进学生思维的生长与发展，提升学生的数学素养。

2基于思维可视化的学科实践路径建构

2.1指向思维可视化的学科实践设计起点：基于课标、教材、学情分析

新课程标准要求强化“做中学”，“做”让思维“看得见”。引导学生参与数学学科探究活动，经历发现问题、解决问题、建构知识、运用知识的过程，体会数学思想与方法，提升解决真实问题的能力。人教版小学数学教材“数学广角”，从学生日常生活中选材，如路灯安装、花坛摆花、道路旁植树、沏茶、烙饼等，在实际生活问题的解决过程中渗透数学思想与思维方法；有部分内容增加了阅读资料，介绍了有关数学知识，渗透了数学文化，如古代的数学问题“鸡兔同笼”等。“数学广角”突出在数学操作中进行数学思考，在可见的活动中学习。如在“找搭档”游戏中思考排列组合，在“田忌赛马”过程中思考数学优化，在探究“鸡兔”各多少只的活动中体会假设法的应用等，在具体探究实践过程中形成理性思维。

对于“鸡兔同笼”的教学内容，不同版本教材编排年级、体例、呈现的问题解决方法有别，表2为各版本教材“鸡兔同笼”问题分布情况及解决方法。

“列举”让思维“看得清”。9种教材都把此内容作为独立的学习主题，呈现了“列举法”这种基本的问题解决策略，体现了“猜想—比较—推理—调整”探究过程。人教版（2014）将内容安排在四年级下学期，以列表比较、画图表征为基本特征的“可视化”平台，使学生在具体的“猜想—比较—调整”过程中感受“鸡兔”头与脚数量的变化规律，深度理解抽象的“假设法”的本质（列举法与画图法都体现不同层次的假设思想）。

“假设”思想分学段渗透，让想象思维逐渐“看得远”。用列表假设法进行实践探究，是用数学学科特有的方式进行活动，有鲜明学科实践的特点。假设是一种预见与猜想，是有意义的高阶思维，也是一种问题解决的重要思想方法。小学阶段，基本上是在具体真实的情境中假设，假设的过程与结果常以具体的图像、图表、符号、数值等方式表达，是一种具体化的假设，是在数学学科实践活动中假设。学生从一到六年级数学学习过程中贯穿了“假设法”或假设的思想，表3为学生在各学段运用假设法的情况。

由此可见，学生从一年级开始接触假设法，但很隐蔽。假设法与具体操作结合，用图表、算式等方式表达假设法的过程，将抽象的推理转化为便于理解的具象，由图表到抽象的符号，层层递进。

九种教材中，人教版教材最早安排“鸡兔同笼”假设法解决问题，并以此构建问题模型思想。四年级是一个承上启下的过渡年级，虽然学生的逻辑思维能力不断发展，推理意识逐渐增强，但是形象思维在问题解决中仍占有重要地位。调查发现，在课堂学习前，有近30%的学生以“试”“猜”的方法找到数字较小的“鸡兔同笼”问题的正确答案，能找到数字稍大的“鸡兔同笼”问题的人数仅为10%左右。由此表明，“试”也有方法，盲目地“试”对复杂问题的解决作用不大。学生需要在不断猜测中获得确定的规律，应用规律解决问题，实现“不试”或科学地“试”。“鸡兔同笼”的学习，使学生借助列表特例进行尝试与探究，发现隐含的替换规律，明确“画图”“列举”“假设”等方法间的内在联系，进而真正理解假设法原理，推动思维发展。

2.2围绕数学问题解决：基于思维可视化的数学学科实践的实施路径

学科实践是学科学习方式，学生在主动探索、积极参与学科问题解决的“类实践”学习活动中，发展知识理解等关键能力，实现素养转化[6]。 “情境参与和问题解决是实践学习方式区别于其他各种学习方式的基本特征。”[7]数学学科问题是实践学习的导向，问题解决是实践学习的基本任务。学生在真实有意义的情境中，以学科问题激活学生认知及探究的心理，在问题解决的过程中理解知识、应用知识和获取新知识。

2.2.1问题表征，思维驱动

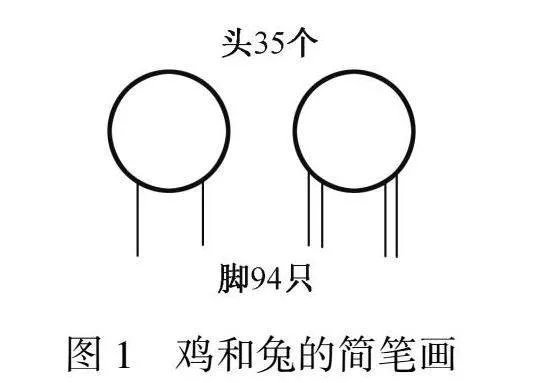
问题解决时，对问题涉及的对象、条件、目标等方面，用文字、图表、符号或模型等具体和通俗易懂的方式表现出来，驱动大脑对问题进行相关信息的记载、理解和表达等思维活动，建立起问题表征。问题解决前，对问题信息与问题本身进行表征，能有效促进问题解决策略的选择与应用。问题表征是一种对问题情境和结构进行心理加工的过程，贯穿问题解决全过程，很大程度上影响问题解决的难易程度。教师进行“鸡兔同笼”教学时，出示《孙子算经》，多媒体演绎主题图；学生模仿图中小孩苦想的情境，并有感情朗读，在感悟题目含义时，体味了古代文化之美。学生被激发了解决问题的兴趣，发现了题目隐蔽的信息：一只鸡比一只兔少两只脚。教学PPT呈现鸡免的简笔画，如图1所示。教师提问：“如何才能算猜对呢？”此问题推动了学生进一步表征问题的内在关系：鸡、兔的头之和为35个，脚一共94只。问题解决过程中，有的学生列举错误，“顾头不顾脚”，或“顾脚不顾头”，其根本原因在于对问题信息表征的错误，没有将题目信息建立关联，形成“头、脚”的信息结构，建立正确的数量关系，也缺乏用数学的眼光观察与分析问题的能力。

根据图式理论，结构良好的图式能够帮助学生识别与构建问题情境中的数量关系，有效运用已有的数学知识、思想方法，多元表征问题结构，如用列举、画图、算式等方式表征信息与问题的关系，让数学操作更有趣味与吸引力，同时驱动了思维的可视化发展，降低了问题解决的难度。

2.2.2问题探究，思维可视

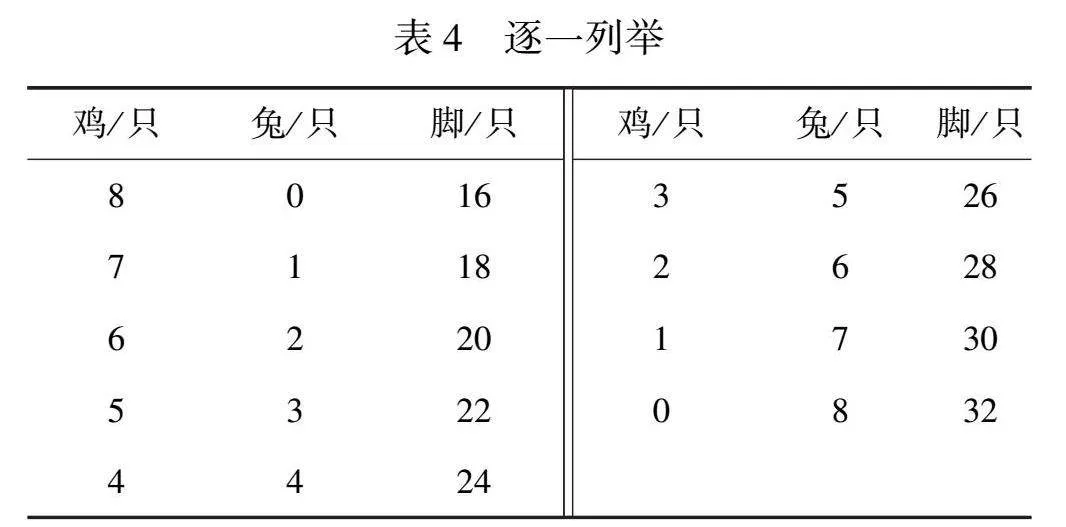
问题引领，动手操作，逼近本质。学科实践的显著特点是动手操作，不仅有实物操作、表象操作，还有符号操作，即用双手去做、用大脑去想、用眼睛去看等。“鸡、兔各有几只”问题的解决，主要借助符号操作。学生从最初的无序猜想，到有序列表；从逐一列举（如表4）、跳跃列举（如表5），到最后取中列举（如表6），在一系列的自主探究活动中，感受到假设法从本质上看就是特殊的列举法。从数据调整的变化过程中，学生探寻鸡兔的头、脚间的变化规律，发展逻辑思维能力。在解决“8只头20只脚，鸡兔各几只”时，从8只鸡0只兔共16只脚开始列表，添4只脚就达到脚总数20只的题目要求。由“怎样添”“理由是什么”的问题，引发学生讨论“将1只鸡换成1只兔”后脚的变化规律：每换1只，脚增加2只。借助画图解释猜测的过程（如图2），用圆圈加两条线作鸡腿，画出形象的鸡，再加两条线（兔腿）变成兔，让思考可视化，从具体到抽象恰当解释了跳跃列举和中间列举法的合理性。

认知体验，思维贯通，知识建构。课堂中解决“鸡兔同笼”问题，学生从未知开始，在“猜”的过程中用画图、列表、验算等最原始的“笨”方法，逐渐体验“猜想—对比—调整”的推理过程，不断积累学习经验，在实践探究中一步步优化思维方式，实现了由一一列举到取中列举、由画图到列式、由猜到算等问题解决方法的转化，建立假设法的运算模型。以“对比”的方法关联知识结构，发展学生数学理解力。对比与反思“列举、画图、假设”3种方法的异同，揭示3种方法之间的内在联系。列举是一种特殊假设，画图是直观体现列举、假设的过程，其本质上是一致的，都是假设法的不同形式的体现，实质都蕴含了“假设—验证—调整”循环往复的思维过程。

分享交流，展示过程，拓展思维。语言是思维的外壳，用自己的语言表达“怎样想”“为什么这样想”“想的结果是什么”等问题，这是具有数学学科特点的语言实践活动。学生用自己的语言表述思考的过程：假设全是鸡，则脚有8×2=16（只），脚少了26-16=10（只）；一只鸡换成一只兔脚多了2只，则要将多少只鸡换成兔？10÷（4-2）=5（只），即兔有5只，鸡有8-5=3（只）。最后，学生归纳了此类问题用假设法解决的基本流程。学生用自己的语言、图式、算式等方式表达自己的思维过程，总结、提炼问题解决的方法，并分享给其他学生，以体验成功的喜悦，不断积累思考的原动力。课前，独立用各种方法猜测、验证答案；课中，小组交流自己的想法，向全班展示分享自己的思维过程，教师追问，引发学生深度思考。整节课，学生通过猜想验证、分享交流、讨论升华的学习活动，理解假设法的内涵。

2.2.3问题迁移，思维进阶

“学以致用”是模型思维能力的体现，学生在实践活动中学习知识，再回归到实践中应用知识。小学数学模型意识主要是指对数学模型普适性的感悟。数学模型思维，是指通过对现实问题进行抽象与推理，建立数学模型，并用数学模型解决类似问题的意识与观念[5]58。学生将生活问题经过“数学化”转化为数学问题，在数学问题解决过程中掌握数学知识，建立数学模型；再用恰当的数学方法与工具，将学习的问题转化为生活问题，与外部世界建立联系，实现数学模型向生活问题的拓展与迁移，提升思维素养。

用学科实践的方式学习数学，目的在于让外在的数学知识向内在的素养迁移与转化。学习迁移是学生学校生活学习与真实世界问题解决间的通路[5]60。 “鸡兔同笼”问题蕴含的数学思想主要是假设推理，在几种方法建立关系的过程中，理解假设法的本质“假设—对比—调换”，把握了假设思维的“神”；从直观到建构，初步感悟了假设法的数学模型，得到了假设思维的“形”。再演绎到“龟鹤”“三轮车和自行车”“植树”“买票”等新的生活问题，引导学生认识到在具体生活实践中，很多新问题的解决都可以用这种“尝试—调整”的思维方式，假设思维“形神”完美相遇，数学模型灵活运用。让学生将问题模型应用到生活问题的解决中，从问题解决走向思维建构，发展了学生用数学的眼光观察现实生活、用数学的思维分析生活问题、用数学的方法解决实际问题的数学核心素养。

3正确处理好两对关系，聚焦学生素养提高，提升学科实践的实效性

多次轰轰烈烈的课改，取得了很大成就，同时由“满堂灌”到“满堂问”、由“自主”变“自流”、教师由“演员”变“观众”、课堂由缺乏探究到无探究不成课等极端现象也不少见，严重违背课改初衷，影响课改质量，给课程研究与实践者诸多教训与思考。本次课改试图以学科实践为支点，撬动育人方式的变革，让“自主、合作、探究”迭代升级，构建实践育人新模型，学科实践在新课改中焕发新机，充分发挥“做中学”的应有价值。但是，如果处理不好传承与改革、“为什么要改”“要改什么”“要改到什么程度”三者关系，过分偏向一种学习方式的正面而忽略观察它的反面，也会重蹈复辙，不利于学生学科核心素养的发展。在提倡以学科实践学习方式促进思维可视化的同时，需要聚焦学生素养的提高，正确处理学科实践、思维可视化与核心素养的关系，以提高教与学的实效性。

3.1正确处理学科实践与学习方式多样化的关系

3.1.1学科实践学习不是数学学习的唯一方式，也不是思维可视化的唯一道路

数学知识的多样性与知识构建的复杂性决定了学习方式的多样性。实证研究发现，样例学习、发现学习（类似于实践学习）和观察学习，3种学习方式均有助于学生对技能要素的迁移，而样例学习更有xFulXOgGGIq/OKsvQsES1w==助于原理关系和解题策略方法的迁移；学生先前知识经验较为丰富且能与要学习的新知识建立起联系时，发现学习对于促进学生概念理解的优势才能被凸显，如缺乏教师指导，对学习程序性知识没有优势；观察式学习不利于概念性、程序性知识学习[8]。由此可知，实践学习方式不是数学学习的唯一方式。有的概念学习，如小数、分数等，也可用接受式学习，用概念同化方式把新概念纳入学生原有认知结构中去理解，如在整数概念基础上认识小数，用新概念的实质性意义，改善原有的认知结构。“鸡兔同笼”的学习，渗透了多种学习方式，如学生展示列举法时，学生同时采用了观察学习方式和样例学习方式等。同样，思维可见，不仅可以将思维的过程与结果“做”出来，还可以“说”出来、“画”出来等。需要根据学习的内容及学习对象的特点灵活选择可视化的方式，提升学习效率。

3.1.2研究适合学科实践学习的内容与对象特点，恰当运用思维可视化方式

学科实践不是万能的，有其适用的内容与对象。教学时，需要从育人体系的角度系统设计课程，避免虚假、浅层次的学科实践。深入分析学习内容，哪些内容适合学科实践，以什么方式进行实践；哪些知识不利于实践学习，需要站在前人或自己的肩上学习。否则，数学学习将会走向另一个极端，进入“实践化”胡同。若所有内容都运用“综合实践”式学习方法学习，将会大大降低学习实效性。除了分析教学内容和学科结构外，还需要分析教学对象——学生的知识结构、心理特点，合理选择学习方式，分析教师怎样介入发挥引导作用，以思维可视化促进学生思维发展，而不仅是学习方式的运用。

3.1.3正确评价学习效果，以效果反馈调整学习方式

基于数学学科实践学习的“操作探究”的特点，对实践活动的评价侧重在表现性评价，评价维度注重数学观念态度、数学思维变化等。设计测评量表将数学核心素养转化为可测量的外显行为，实现从“知识测评”转向“素养测评”，发挥评价的诊断与导向功能等，优化思维可视化学习路径的设计，提升学习效率。

3.2正确处理思维可视化与思维内隐性的关系，避免为“可视”而“可视”现象

数学学科实践是一种很好的思维可视化途径。在实践过程中，数学知识由抽象转化为形象直观，将内隐的数学思维变得可视化，有利于知识的掌握、技能的形成。从认知心理学的角度认识思维，思维是人脑中的内部加工活动，具有很强的内隐性，有的是只可意会无法言传，凭直觉认识、靠无形顿悟的内在思维活动；也有的是潜在的目前没有表现出来的思维过程或结果。数学学科实践，重点是具身体验，没有必要将所有过程都可视化，如数感、量感等，通常是一种直觉的感悟，在实践活动中形成，但要学生用什么形式体现他的感悟，确实很困难。因此，不必强行“实践”，或为了“可视”而“可视”，忽略了学习效果。

4结语

数学学科实践顺应时代发展，回答数学应“怎么教”“怎么学”等问题，将认知与行动联结，实现从知识教学转向学科育人。同时，以实践方式实现了思维可视化，体现数学学科特点。应恰当运用数学学科实践，发挥综合育人作用，助推每位学生在数学上得到不同发展，逐渐形成适应终身发展需要的核心素养。

参考文献

[1]袁利平，杨阳.施瓦布的“实践”概念及课程旨趣[J].全球教育展望，2020，49（1）：17-26.

[2]谢绍平.浅析探究式教学与实验教学、启发式教学的关系[J].教学研究，2019，42（2）：96-100.

[3]李艳，陈虹宇，陈新亚.核心素养融入的中国研学旅行课程标准探讨[J].教学研究，2020，43（3）：76-85.

[4]哈蒂.可见的学习（教师版）——最大程度地促进学习[M]. 金莺莲，洪超，裴新宁，译.北京：教育科学出版社，2015：78-113.

[5]刘艳.学科实践：作为一种学科学习方式[J].教育研究与实验，2022（1）：57-63.

[6]郭元祥.论实践教育[J].课程·教材·教法，2012（1）：17-22.

[7]魏瑞霞.为“问题解决”而教：小学数学模型思维教育实践[J].人民教育，2022（10）：56-58.

[8]张春莉，宗序连，邓惠平，等.不同学习方式对小学生数学知识建构的影响[J].教育研究与实验，2021，201（4）：77-82.

Literacy-oriented discipline practice： the realization path of thinking visualization—take the teaching of “chicken and rabbit with the same cage” as an example

TANG Bin，WANG Jing

（The Primary School Affiliated to Wuhou Experimental Middle School，Chengdu， Sichuan610043，China）

Abstract

Over the past two decades of mathematics curriculum reform，the traditional “teacher-centered lecturing” classroom format has undergone significant changes，but the phenomenon of superficial inquiry remains prominent. The new curriculum reform advocates learning through practical activities，emphasizing the presentation of both the thinking process and its results，aiming to upgrade the concept of “inquiry-based learning.” Mathematical practices serve as one of the pathways to make thinking visible，thus highlighting the educational value of these practices.With a precise understanding of curriculum standards，textbooks，and student needs，diverse practical approaches make thinking“visible”“clear”and“far-reaching.”Centered on problem-solving and guided by it，real and meaningful contexts are created to stimulate students’ cognitive and inquiry processes.Students are guided through visual processes such as problem representation，strategy exploration，method transfer，and model construction，which contribute to the development of mathematical thinking skills.However，mathematical practices are not the only approach to learning mathematics.Various learning methods should be flexibly chosen according to the content and characteristics of the learners.Effective visualization of thinking should be employed to cultivate students’ core competencies and achieve the educational goals of the subject.

Keywords

core competencies;disciplinary practice;practical education;visualization of thinking;characteristics of mathematics discipline

[责任编辑马晓宁]