基于FFT与Transformer算法的混合期权定价模型研究

摘 要：为解决经典期权定价模型与实际价格数据偏差较大的问题，选取BS期权定价模型，采用快速傅里叶变换（Fast Fourier Transform，FFT）结合Transformer多头注意力机制深度学习算法，对上证300ETF期权与上海期货交易所黄金期权数据进行实证研究，通过改进的Transformer算法对基于FFT算法的期权定价模型与实际金融市场期权价格数据之间的残差值进行二次训练。结果表明，与其他算法（BS、FFT-BS）及其他混合算法（FFT-BS+ARIMA、FFT-BS+LSTM）模型相比，基于FFT-BS+Transformer的算法在R2、MSE、NRMSE以及MAE等统计指标上均有很好的表现，且针对不同波动、不同品种的期权，该混合算法模型均取得了较好的结果。将改进后的Transformer算法应用到期权定价中，可弥补经典期权定价模型的不足，提供了更加精确的期权定价模型。

关键词：计算机神经网络；金融市场；期权定价；深度学习；混合模型；多头注意力机制

中图分类号：F830.91

文献标识码：A

DOI：10.7535/hbkd.2024yx05011

Research on hybrid option pricing model based on

FFT and Transformer algorithm

WEN Wei1，FU Zhiyuan2，ZHANG Yanhui2

（1. School of Economics，Beijing Technology and Business University，Beijing 100048，China；

2. School of Mathematics and Statistics，Beijing Technology and Business University，Beijing 100048，China）

Abstract：In order to solve the problem of the large deviation between the classical option pricing model and the actual price data， based on the BS option pricing model， the Fast Fourier Transform （FFT） combined with the Transformer's multi-head attention mechanism of deep learning algorithm was used to conductthe empirical research on the 300ETF options and Shanghai gold options data. The model was quaeMzbpPpYYZrWjqWjA+zzOGh05mYQsWit5R+XnOHTAVM=dratically trained by the improved Transformer algorithm on the residual values between the option pricing model based on the FFT algorithm and the option price data of the actual financial market. The results show that compared with other algorithms （BS model， FFT-BS model） and other hybrid algorithm models （FFT-BS+ARIMA model， FFT-BS+LSTM model）， the proposed model has a good performance in the statistical indexes such as R2， MSE， NRMSE and MAE， and the hybrid algorithm model achieves a better perf_{lcZKirmhzEy1WXtphXnY6GaS0SAfmljVQTtxYNJJQds=}ormance for different volatilitiesand different varieties of options. The study innovatively applies the improved Transformer algorithm to option pricing， which compensates for the shortcomings of the classical option pricing model and provides a more accurate option pricing model.

Keywords：computer neural network; financial market; option pricing; deep learning; hybrid model; multi-head attention mechanism

中国金融产品发展相对较晚，金融工具创新不足，衍生产品不全，行业对外开放程度也不高。随着金融市场改革进程的加快，在经济“新常态”的要求下，金融行业的发展尤其是衍生品的快速发展迫在眉睫。期权定价一直是衍生品的核心研究问题之一。自Black-Scholes-Merton模型[1]问世以来，期权定价问题广受关注，相关模型得到持续改进[2-4]。

Lévy过程的引入，准确地描述了资产波动情况[5]，有效反映了资产价格服从非高斯分布及跳跃行为[6]。在期权定价数值计算方面，目前使用较多的方法有二叉树法[7]、有限差分法[8]和快速傅里叶变换法（Fast Fourier Transform，FFT）[4]。CARR等［8］使用FFT提高了计算速度和逼近精度，对任何特征函数，得到一个简单的解析表达式，利用FFT对期权价格或其时间价值进行数值求解。该方法后续被广泛应用于各类复杂期权定价模型计算，随后又出现了分数阶傅里叶变换求解期权模型［9］，效率更快。

近年来深度学习等算法的出现为传统的期权定价模型提供了新思路[10-13]。深度学习模型框架Transformer摒弃了递归（RNN）和卷积（CNN），完全基于Attention多头注意力机制，有效处理时序数据，如自然语言、图像、视频等[14]。现在流行的Bert模型和GPT模型均使用了Transformer的网络结构，其中使用双向Transformer编码器预训练大规模的文本语料，被广泛应用于文本分类、命名实体识别、系统问答等[15]；GPT使用了单向Transformer编码器生成文本，用于文本摘要、对话生成等任务[15]。但这些算法以及深度学习模型单一使用时均出现局限性。例如：金融市场存在交易博弈，基于无风险套利原理的传统期权定价模型对于实际金融市场期权数据的预测精度有待提高；深度学习模型往往只能描述数据之间的相关性，对于数据之外客观事实影响因素的分析并不理想。另外，如果只通过单一的机器学习方法或深度学习方法对价格数据进行时序预测，其结果往往不具有较强的解释性和稳定性。为此，有的科研人员引入混合期权定价模型进行实证研究，对芝加哥交易所和美国期权交易所内多个期权品种进行对比验证，结果表明混合期权定价模型能有效解释偏差，估值比较准确[16]；有的使用期权定价模型与神经网络模型构建混合模型，分别在悉尼期货交易所和中国期权市场进行实证研究[17-19]；有的使用小波网络和遗传算法对中国香港期权建模[20-21]；还有的通过深度学习模型优化期权定价模型计算方法[22]。

本文假设资产价格过程服从几何布朗运动，仅讨论欧式看涨期权的合约定价，不考虑期权交易成本，欧式看涨期权多头收益为max

{ST-K，0}，其特征函数如式（1）所示。从算法设计入手，介绍基于FFT的期权定价模型以及改进的Transformer网络结构，通过构建FFT-BS-Transformer混合模型，给出相应模型输入与输出过程数据的处理方案，并针对中国国内金融和商品期权进行实证对比分析。

ΦT（u）=eiu（ln S0+（r-σ22）T）-σ2u22T。

（1）

1 算法设计

1.1 基于FFT的期权定价模型（FFT-BS模型）

在BS模型中，假定资产价格St服从几何布朗运动，根据ROSS[23]和COX等[24]的理论，在T时刻的欧式看涨期权价格，等价于计算资产在风险中性测度Q下的贴现期望，即

V（St，K，T）=e-r（T-t）EQ［W（ST）］， W（ST）=max{ST-K，0}=（ST-K）+ 。（2）

式中：V（St，K，T）为期权价格；r为无风险利率。用CT代替式（2）中的V（St，K，T），

CT（K）=e-r（T-t）EQ［W（ST）］=e-r（T-t）

∫+∞K（ST-K）+qT（x）dx 。（3）

将ST、K进行替换：

CT（k）=e-r（T-t）

∫+∞k（ex-ek）qT（x）dx 。（4）

式（3）和式（4）中：qT（x）为资产分布的风险中性概率密度函数，即dQ=qTdx；ST为T时刻资产价格；K为期权到期日执行价格；x=ln ST。

由于limk→-∞CT（k）=S0[9]，CT（k）不满足平方可积条件，无法直接使用FFT，因此引入调整变量α，记

cT（k）=eαkCT（k）， α>0 。（5）

由文献[9]有：

CT（k）=e-αk2π

∫+∞-∞

e-iukφT（u）du=e-αkπ∫+∞0

Re［e-iukφT（u）］du 。（6）

式中：φT（u）为cT（k）的傅里叶变换；Re为对结果取实部。

1.2 Transformer网络结构

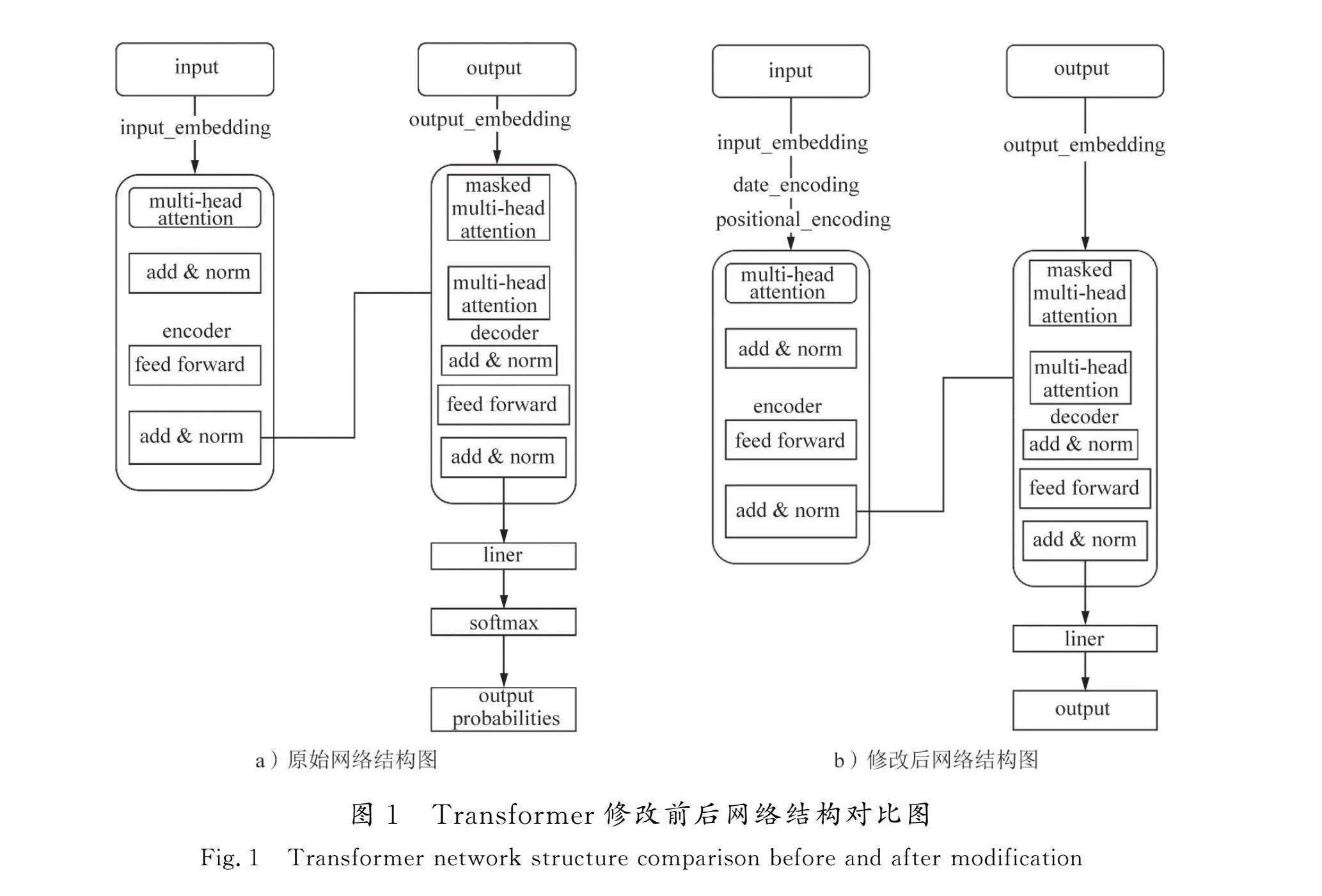
Transformer是一种基于注意力机制的网络结构，与传统CNN和RNN模型相比，Transformer的多头注意力机制以及位置编码机制，能有效解决传统深度模型以及计量模型中随着序列数据长度的增加，预测数据与较远数据相关性较低，容易受近期数据的影响导致预测不准确的问题[13]。同时，由于编码机制的存在，对于时序数据中周期性数据关系、季节性数据关系，Transformer模型预测效果更好。Informer模型[25]在Transformer模型基础之上添加了日期编码，同时改进了多头网络结构，在时序数据预测方面表现更加优秀。

自注意力机制作为多头注意力机制的基础，对于向量［a1，a2，a3，a4］，存在矩阵Wq、Wk、Wv，求解获得新的向量qi、ki、vi，计算过程见式（7）—式（9）。

qi=Wqai 。（7）

ki=Wkai 。（8）

vi=Wvai 。（9）

以获得的q1为例，分别与［k1，k2，k3，k4］相乘，可获得［α1，1，α α1，3，α1，4］

（注意力分数）。同理，对q2、q3、q4进行同样操作，可以获得注意力分数矩阵。将注意力分数再次进行Softmax操作归一化，便可以获得最终的系数矩阵，见式（10）。

α1，1…α4，1

α1，4…α4，4=

［k1，k2，k3，k4］′×［q1，q2，q3，q4］ 。（10）

将获得的系数矩阵与v相乘，最终式如下。

［b1，b2，b3，b4］=［v1，v2，v3，v4］×

α1，1…α4，1

α1，4…α4，4 。（11）

相比循环神经网络，自注意力机制对于长序列并行度更高，且自注意力机制最大路径长度更短，因此自注意力机制优于传统循环神经网络系统。

多头注意力分出多支，一般在使用过程中默认参数为8。为简化介绍多头注意力，在此以两头注意力为例，见式（12）—式（14）。

qi，1=Wq，1ai， qi，2=Wq，2ai 。（12）

ki，1=Wk，1ai， ki，2=Wk，2ai 。（13）

vi，1=Wv，1ai， vi，2=Wv，2ai 。（14）

相比单头自注意力机制，多头注意力需要在［qi，ki，vi］基础之上分别计算出qi，1、qi，2、ki，1、ki，2、vi，1、vi，2。因此，bi，1由qi，1、ki，1、vi，1计算而得，bi，2由qi，2、ki，2、vi，2计算而得。最终bi由bi，1、bi，2合并再与权重矩阵相乘，使得最终bi维度与单头自注意力机制所得bi维度相同，注意力计算式如下：

Attention（Q，K，V）=Softmax（QKTdk）V 。（15）

利用Transformer模型预测，有2种常用方法。一是对时序数据直接进行预测，以时间T时刻为例，将T时刻之前的历史数据作为模型输入项，将T时刻数据作为预测数据代入模型，进行模型的训练与预测；二是以截面数据作为模型的输入输出项，同样以T时刻为例，将时刻T对应的相关性影响因子作为模型输入项，期权价格作为模型输出项，以此构建模型进行训练预测。本文采取第1种方式作为Transformer模型的训练预测方法。传统Transformer模型擅长处理分类数据，不擅长对连续型变量的预测，所以需要对该模型进行调整，来适应当前的场景。调整方向主要分3部分。

1）输入数据，网络结构调整。原始模型中输入数据是离散型数据，因此模型的输入需要对离散型数据进行分类编码。本文输入数据为连续型数据，因此原始模型中编码方式不再适用。原始数据进入本文模型前，需要对其进行标准化处理，然后直接采用convld层替换原始embedding层，将原有编码分类结果替换为连续型变量输出。

2）输出数据，网络结构调整。由于原始模型中输出结果为分类结果数据，因此在经过全连接层后还需要进行Softmax层的处理。由于输出结果为连续型数据变量，因此在网络结构上取消了Softmax操作，直接将全连接层输出结果作为最终结果。但由于模型变量在输入开始阶段进行过标准化数据处理，因此需要对模型结果进行反向标准化处理。本文数据标准化处理公式为z=x-μσ，其中μ为变量均值，σ为变量标准差，x为变量原始数值，z为标准化处理后的数值。

3）输入项添加到期日数据。金融数据具有明显的周期性、季节性等时间特性，期权价格数据受到期日时间长短的影响。因此，对于期权价格序列预测，需要在原有位置编码的基础上添加到期日数据。具体操作为对到期日期采用embedding层的处理方法，将到期日特征值进行编码添加至原始输入当中。

位置编码公式为PE（pos，2i）=sinpos10 0002imodel，

PE（pos，2i+1）=cospos10 0002imodel。

其中pos为输入数据位置位次数值。到期日编码公式为e（x）=W×x。

Transformer修改前后网络结构对比图见图1。

由图1可知，与传统计量模型或者深度学习模型相比，Transformer模型在输入项中多出一项decoder层的输入。本文decoder层输入参照原始模型输入，保留encoder输入的一部分数据，同时将预测长度数据全部补充为0，上述2部分数据组合作为decoder层的输入部分。

模型损失函数定义如下：

损失函数=（xn-yn）2 。（16）

式中：xn为预测值张量；yn为真实值张量。本文将原始Transformer模型中使用到的交叉熵损失函数替换为均方误差损失函数，使模型能够处理连续数据。

采取Adam（adaptive monent estimation）参数优化算法[26]，通过计算梯度一阶矩与二阶矩，自适应调整学习率，加快参数更新，提升模型训练效果。该优化算法结合RMSProp和动量算法的优点，在深度学习参数优化中得到广泛使用。模型中学习效率参数LR=0.000 1。

2 模型构建

以预测真实期权市场价格数据为目标。将真实期权市场价格数值分为2部分：一部分通过使用FFT计算获得经典期权价格；另一部分以真实期权市场价格与上述模型的差值定义为残差，该值作为改进后的Transformer网络训练拟合目标。最终期权价格为上述2个子模型结果的和，表示为FFT-BS-Transformer。模型结构图如图2所示。

模型预测的评价指标如下：

R2=∑ni=1（yi-）2

∑ni=1（xi-）2，

yMSE=1n∑ni=1（yi-xi）2，

yNRMSE=yMSEmax xi-min xi，

yMAE=1n∑ni=1

|yi-xi|，

yMAPE=1n∑ni=1

yi-xixi。

式中：R2为决定系数；yMSE为均方误差；yNRMSE为归一化均方根误差；yMAE为平均绝对误差；yMAPE为平均绝对百分比误差；x、y分别代表通过交易所获得的实际期权价格以及通过模型计算获得的预估期权价格；为x的均值。

3 实证分析

为验证所选模型的普适性与准确性，选择金融与商品2种欧式期权进行实证分析。沪深300作为唯一在上证、深证以及中国金融期货交易所上市的指数类期权，是沪深市场最具代表性的指数。黄金是国家和普通投资者资产配置的重要品种之一，具备货币、金融和商品的属性，是在大众商品投资中认可度最高、交易最为活跃的投资品种。

本文选取沪深300ETF期权和黄金期权作为模型实证标的，交易周期选取2022年10月至2023年3月，数据频率采用日线数据，数据来自wind数据库。采取上述2类品种原因如下：首先，沪深300期权以现货ETF为基准，黄金期权则以黄金期货为基准，标的物不同；其次，沪深300是金融类期权，黄金期权为实物类期权；最后，两者波动性不一致，相关性较弱。

此外，添加几组不同模型进行对比。模型1：BS模型[1]；模型2：以FFT为计算方式的BS模型，记作FFT-BS模型[9]；模型3：FFT-BS模型+ARIMA模型[19]；模型4：FFT-BS模型+LSTM神经网络模型[19]。模型1和模型2验证FFT计算方式对BS模型计算精度是否有所损失；模型3通过FFT-BS模型与传统计量模型ARIMA模型组合，验证传统计量模型是否对残差拟合有所帮助；模型4用于对比Transformer模型相对传统深度学习模型是否在统计数值上有明显的提升。

模型当中资产波动率数据是非常重要的，对于模型计算结果影响较大。本文所有模型波动率数据都采用滚动计算标的物历史波动率作为输入项。以T时刻为例，当前时刻T之前20个交易日的波动率数据的平均值作为T时刻波动率数据。无风险收益率数据以2.1%（区间内国债收益率平均值）为准。

LSTM超参数设置如下：input_size=1（输入变量每行输入数据维度）；hidden_size=24（隐含层的特征数量）；num_layers=1（隐含层层数）；output_size=1（输出向量长度）；seq_length=10（输入序列长度）。为保证测试条件一致性，ARIMA模型、LSTM模型和Transformer模型训练数据长度均为10，即通过10个时序数据预测第11个点数据。为避免模型出现过拟合，实证过程中以验证集数据的损失函数值是否持续减少作为模型是否停止训练的标准。本文中采取的容忍度为7，即当连续7次训练模型均在验证集数据表现不能更好的时候，模型便停止训练。模型实证过程中，全部数据按7∶1∶2随机分配的方式被划分为训练集、验证集和测试集。

沪深300欧式期权实证结果：全量测试数据共计7 025条，训练集数据3 812条，验证集544条，测试集1 090条。由于训练期内存在较多的期权品种，每一个品种前10条数据无法用于训练，因此在数据预处理后，全量数据大于训练数据、验证数据以及测试数据的总和。_{GDDiZvUw8tvs5IVp7OkkINYJozHcUjvHpFPowLb0Ni0=}

原始期权数据的统计描述如表1所示。上海证券交易所沪深300ETF期权交易数据较小，中位数只有0.179，同时残差数据中位数只有0.04。因此，单位数据差值相对于沪深300期权比例来说更大，结果预测的微小波动更容易造成预测结果百分比例的偏差增大。

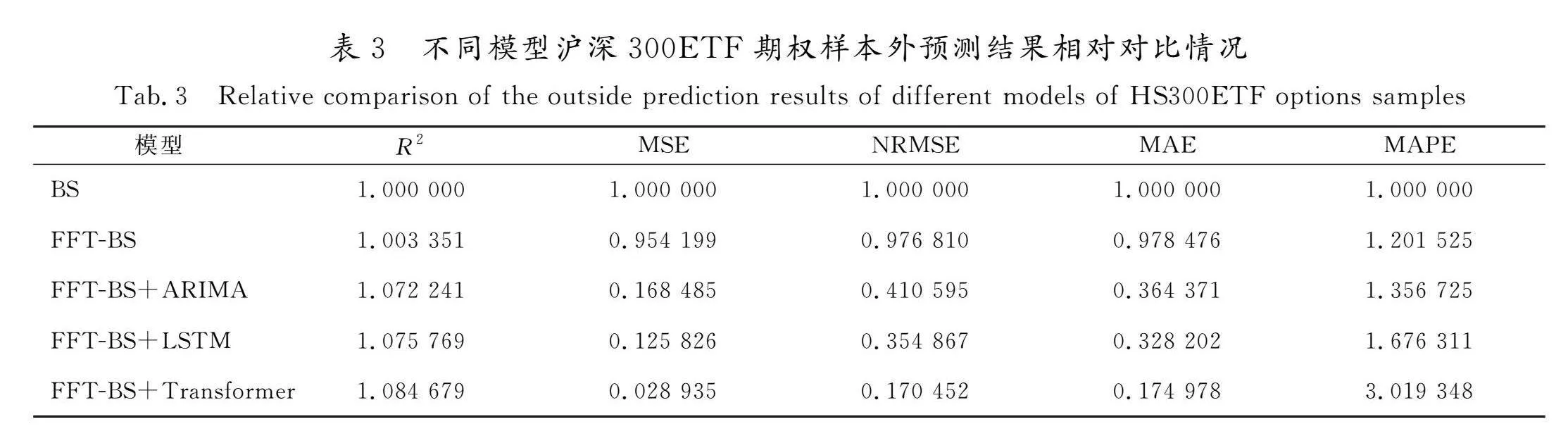
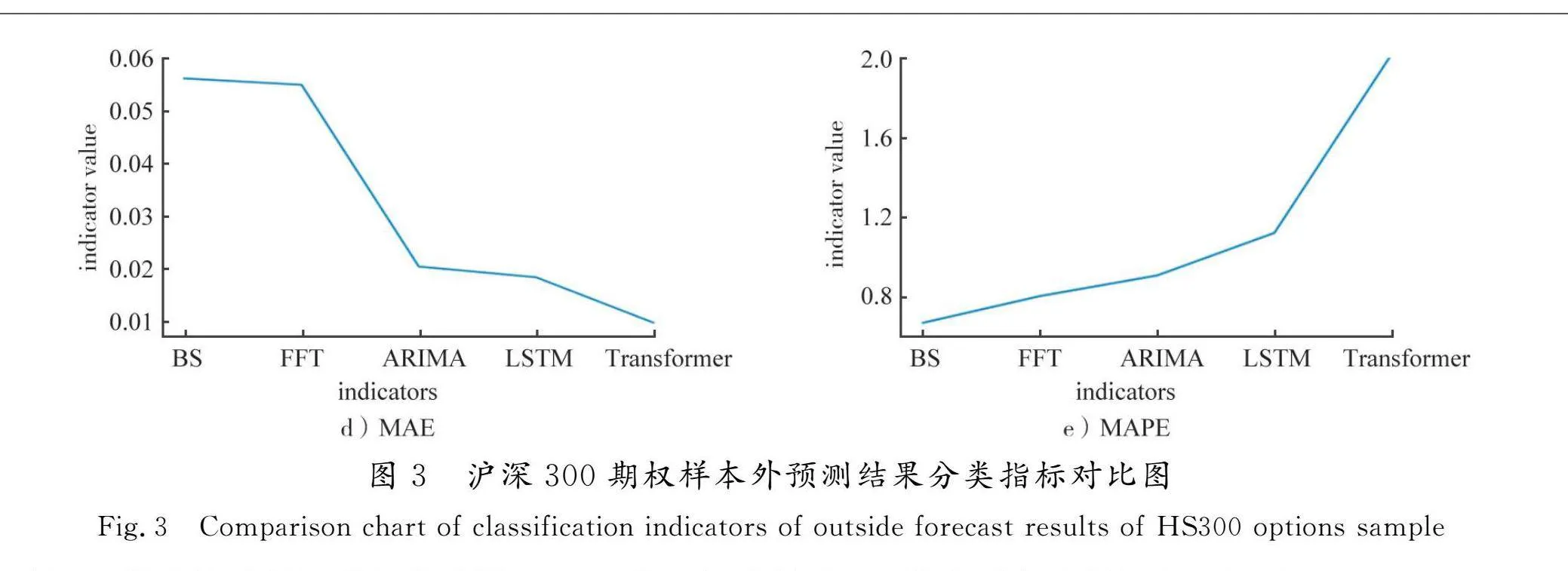
实证结果统计见表2，统计对比了5种不同指标下不同模型的表现情况，绘制各指标结果见图3。

将BS模型统计指标设为基准数值1，其他各模型相对BS模型百分比例如表3所示。

从统计指标维度上分析，上述5个模型在R2、MSE、NRMSE、MAE、MAPE指标中，均呈现出逐步变好的趋势。相比BS模型，本文提出的模型R2增长了8.4%，绝对值约为99.75%；MSE减少了97.2%，绝对值减小至0.000 175；NRMSE减少了82.9%，绝对值减少至0.012 525，MAE减少了82.5%，绝对值减少至0.009 845。

参考其他模型，可以发现随着模型复杂度的提升，模型拟合预测效果越来越好。深度学习模型优于普通计量模型，Transformer深度学习模型又优于以预测时序数据见长的LSTM类RNN模型。这一点与本文模型构建过程中提到的理论依据一一对应。但MAPE指标却表现出相反的结果，该指标相比BS模型增加了2倍数值，但绝对数据仍然较小（2.019 932）。这是由于预测的残差数据较小，微小的数据预测便会带来较为明显的相对值的变化，且对于预测样本而言，预测值越小，其预测得到的结果越容易引起MAPE的变大。

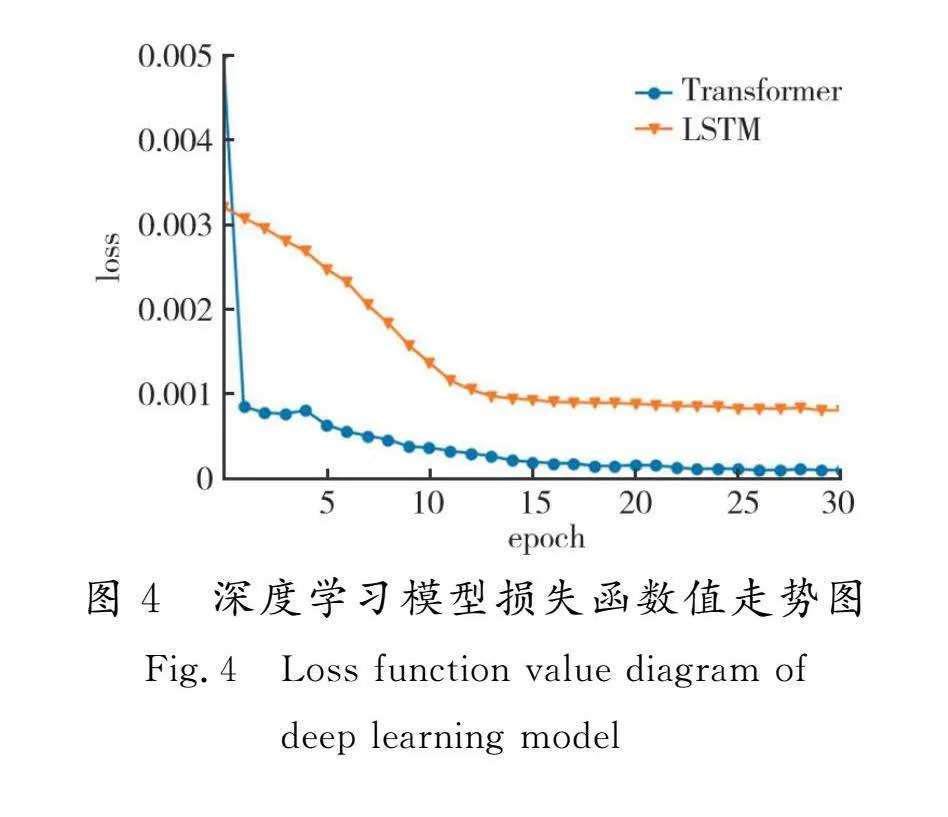
从实际应用交易角度来看，期权价格越小，通常表示该期权价值越低，参与人数越少，市场定价不具有代表性。期权价格越小，该值为非有效数据的可能性越大。因此，本文实证过程中，当把非有效数据剔除后，理论上MAPE指标会有较为明显的改善，单一指标的变差并不影响给出模型整体预测有效性提升的判断。从预测结果统计指标来看，不难发现深度学习模型构建的混合期权定价模型是对比模型中的最优模型。因此，单独将2类深度学习模型训练过程中的损失函数数值迭代图形进行比较，判断两者之间的优劣。

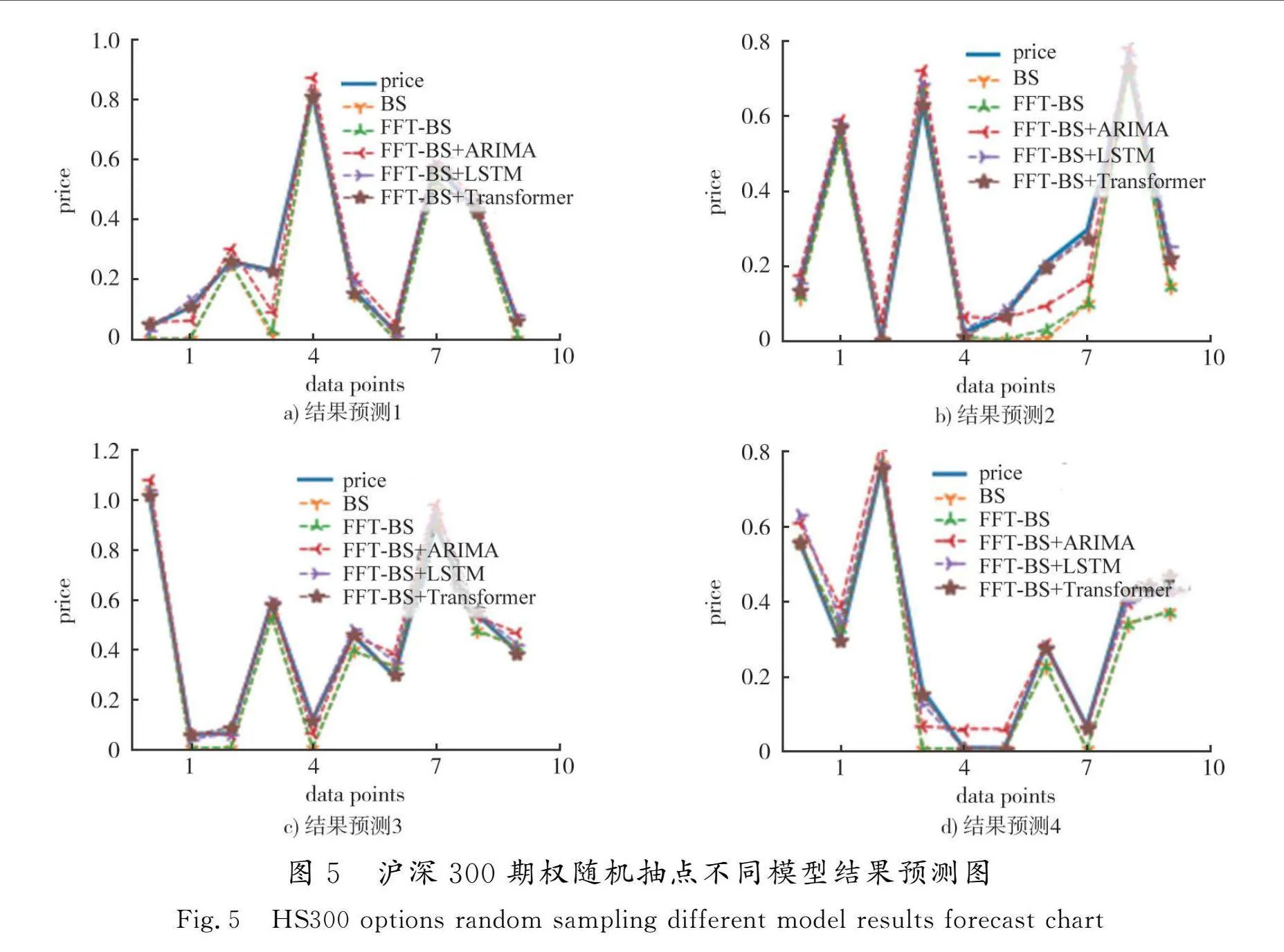
图4为损失函数图形，在同样优化参数情况下，Transformer结构下的模型优化效率更高，需要更少的迭代次数，且模型损失函数值更小，这意味着模型拟合预测效果较好，与上述预测统计结果相符。

从预测结果中随机抽取10组数据，对比不同模型预测结果数据大小，结果见图5。price曲线为实际期权价格，从图5不难发现：FFT-BS具有较高的计算效率以及计算准确性，其计算结果与BS模型计算结果基本一致；与单一模型相比，3个混合期权模型均有较为明显的预测提升，但对于个别时点，如图5中右侧2个小图，Transformer的混合模型预测结果与原始数据更为贴合。

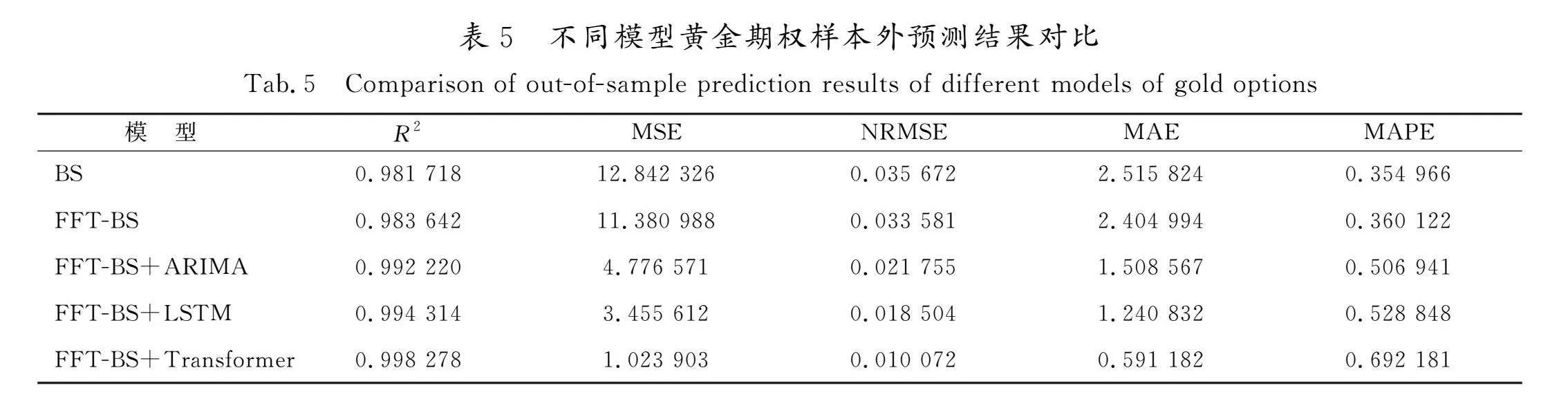
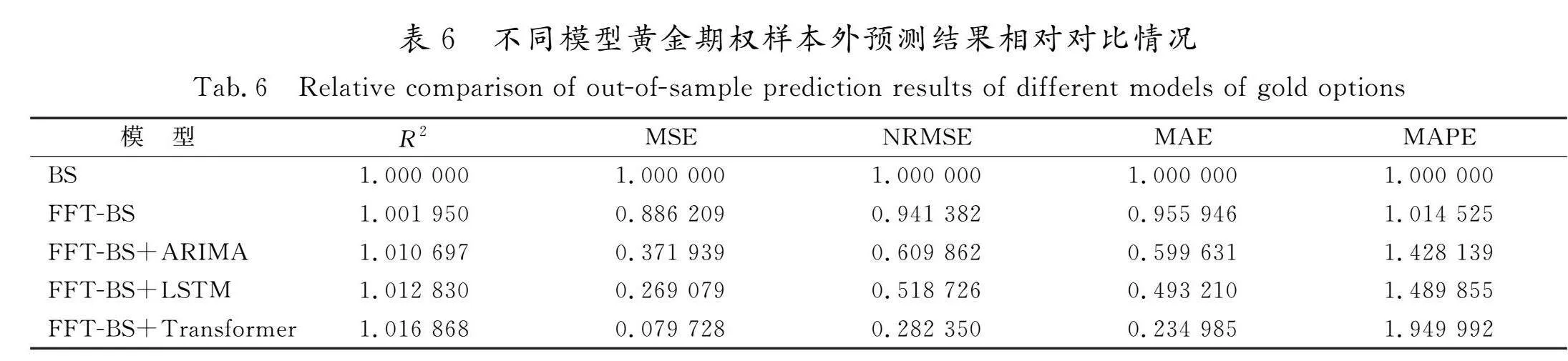
黄金期权实证结果如下：全量测试数据共计11 758条，训练集数据6 556条，验证集936条，测试集1 874条。对比表4和表1可知，相比沪深300ETF期权，黄金期权明显波动更大，平均值、各项分位数均有较为明显的数值差异。单位数据的变动对于黄金期权产生的影响弱于沪深300期权，黄金期权相比沪深300ETF期权更容易被拟合预测，不同模型黄金期权样本外预测结果对比见表5，不同模型黄金期权样本外预测结果对比情况见表6，黄金期权样本外预测结果分类指标对比见图6。

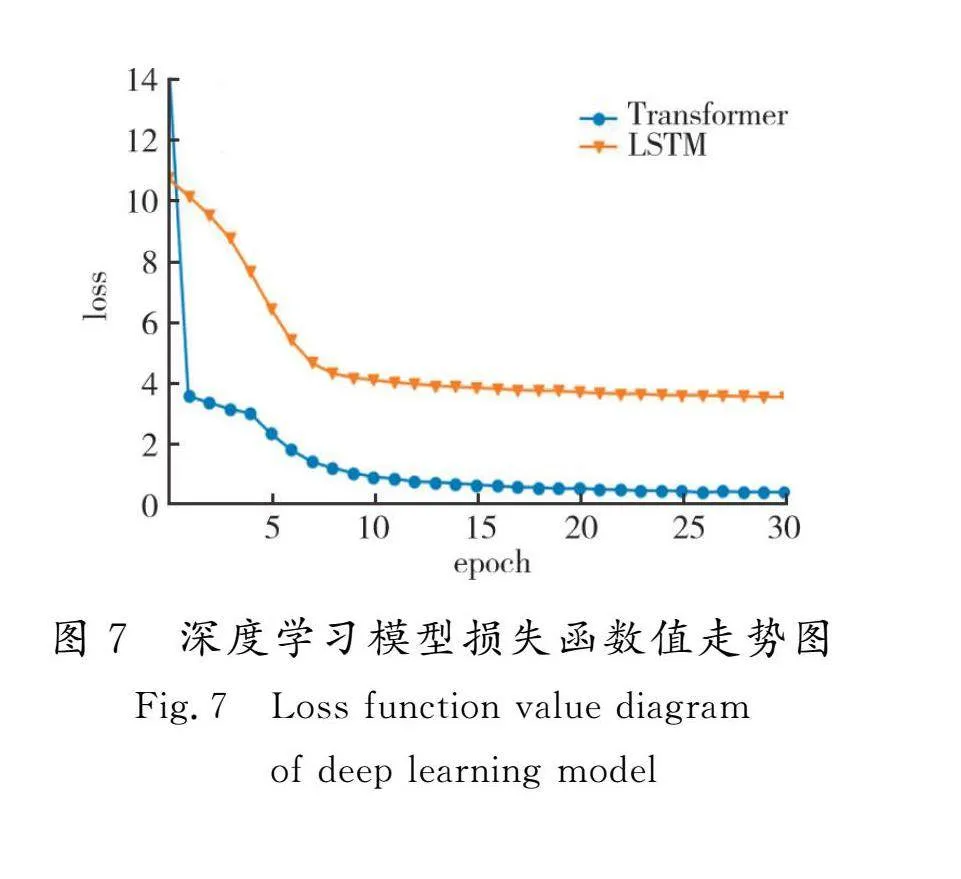
从预测结果统计指标来看，Transformer构建的混合期权定价模型依然是对比模型中表现最优的。相比BS模型，R2提升1.6%，升至约99.82%；MSE直线下降92.0%，降至约1.02；NRMSE下降71.7%，降至0.01；MAE下降76.5%，降至0.59；MAPE同样上涨94.9%，升至0.69。但是对于MAPE指标来说，黄金期权相比沪深300ETF期权有更好的下降，MAPE指标由3.01下降至0.69。由于黄金期权价格远大于沪深300期权价格，因此单位价格变动引起的误差变化更小，MAPE指标也更小。除去MAPE指标，R2、MSE、NRMSE和MAE与沪深300ETF期权预测结果表现出一致性，模型复杂性越高，预测效果越好，指标数值越优。

深度学习模型损失函数值走势图见图7。可以看出，Transformer结构下的模型优化效率更高，需要迭代次数更少，且模型损失函数值更小，这意味着模型拟合预测效果较好，与上述预测统计结果相符。

黄金期权随机抽点不同模型结果预测图见图8。图8中随机挑选黄金期权价格，对比不同模型预测差异。可以看出，FFT-BS模型与BS模型大多数情况下能够满足模型预测需求，但仍有较大偏差。混合模型表现优于单一模型，深度学习模型优于传统机器学习模型，Transformer模型是所有测试模型当中的最优模型。

4 结 语

1）基于BS模型、FFT-BS模型、FFT-BS+ARIMA模型、FFT-BS+LSTM模型和FFT-BS+Transformer模型，在欧式看涨期权定价方面对2组不同类型的期权产品进行实证，给出了5个不同的统计指标对比预测效果。结果表明，上述模型均表现出较好的拟合效果。通过构建混合模型，采取深度学习的混合模型有着更为出色的预测表现，且混合模型的提出具有较强的适用性。

2）通过对已有算法的改进，利用2种子模型组合构建混合模型进行期权定价，将人工智能算法中表现出色的多头注意力机制引入期权定价模型中，可提升模型的预测精度。

3）由预测结果统计指标可知，即使数据质量较差的沪深300ETF期权，同样获得了不错的结果表现，模型预测精度并未受到期权数据较小、噪音干扰较大的影响。这与本文提到的模型构建理论基础一一对应。加入Transformer网络结构，通过强大的注意力机制以及位置编码机制，提高了深度学习模型的预测效果，突破了原有损失函数的数值瓶颈，预测效果得到很大改善。

本研究的不足之处主要包含以下2个方面：一是实证品种较少，并未对更多市场及其他期权品种进行普适性验证；二是模型预测周期目前仅考虑下一交易日，并未考虑多周期时的期权定价问题。未来需进一步优化模型参数，提升模型预测的准确性，并验证对比不同定价模型在不同经济体下的表现，全方位比较各类模型的实证效果。

参考文献/References：

［1］ BLACK F，SCHOLES M.The pricing of options and corporate liabilities［J］.Journal of Political Economy，1973，81（3）：637-654.

［2］ HULL J，WHITE A.The pricing of options on assets with stochastic volatilities［J］.The Journal of Finance，1987，42（2）：281-300.

［3］ BATES D S.Jumps and stochastic volatility：Exchange rate processes implicit in deutsche mark options［J］.The Review of Financial Studies，1996，9（1）：69-107.

［4］ HESTON S L.A closed-form solution for options with stochastic volatility with applications to bond and currency options［J］.The Review of Financial Studies，1993，6：327-343.

［5］ CARR P，GEMAN H，MADAN D B，et al.Stochastic volatility for Lévy processes［J］.Mathematical Finance，2003，13（3）：345-382.

［6］ COX J C，RUBINSTEIN M，HALL P. Options Markets［M］.Upper Saddle River：Prentice Hall，1985.

［7］ 约翰赫尔.期权、期货和其他衍生品［M］.北京：清华大学出版社，2009.

［8］ CARR P，MADAN D.Option valuation using the fast Fourier transform［J］.Journal of Computational Finance，1999，2（4）：61-73.

［9］ CHOURDAKIS K.Option pricing using the fractional FFT［J］.Journal of Computational Finance，2005，8（2）：1-18.

［10］FULOP A，YU Jun.Bayesian analysis of bubbles in asset prices［J］.Econometrics，2017.DOI： 10.3390/econometrics5040047.

［11］HUTCHINSON J M，LO A W，POGGIO T.A nonparametric approach to pricing and hedging derivative securities via learning networks［J］.The Journal of Finance，1994，49（3）：851-889.

［12］QI M，MADDALA G S.Option pricing using artificial neural networks：The case of S&P 500 index call options［C］//Neural Networks in Financial Engineering：Proceedings of the Third International Conference on Neural Networks in the Capital Markets.NewYork：World Scientific，1996：78-91.

［13］VASWANI A，SHAZEER N，PARMAR N，et al.Attention is all you need［C］//Proceedings of the 31st International Conference on Neural Information Processing SystemsD.Red Hook：Curran Associates Inc，2017：6000-6010.

［14］DEVLIN J，CHANG M，LEE K，et al.Bert：Pre-training of deep bidirectional transformers for language understanding［C］//Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics：Human Language Technologies.Stroudsburg：ACL，2019：4171-4186.

［15］GULTEKIN N B，ROGALSKI R J，TINIC S M.Option pricing model estimates：Some empirical results［J］.Financial Management，1982，11：58-69.

［16］RADFORD A，NARASIMHAN K，SALIMANS T，et al.Improving language understanding by generative pre-training［DB/OL］.［2023-12-03］.https：//www.cs.ubc.ca/～amuham01/LING530/papers/radford2018improving.pdf.

［17］LAJBCYGIER P.Improving option pricing with the product constrained hybrid neural network［J］.IEEE Transactions on Neural Networks，2004，15（2）：465-476.

［18］LAJBCYGIER P R.Improving Option Pricing with the Product Constrained Hybrid Neural Network and Booting［D］.Melbourne：Monash University，2021.

［19］张丽娟，张文勇.基于Heston模型和遗传算法优化的混合神经网络期权定价研究［J］.管理工程学报，2018，32（3）：142-149.

ZHANG Lijuan，ZHANG Wenyong.Option pricing model by applying hybrid neural network based on Heston modeland genetic algorithm［J］.Jonrnal of Industrial Engineering/Engineering _{LEtG/5P7shSXSxdHqtj/7Q==}Management，2018，32（3）：142-149.

［20］张鸿彦，林辉.应用混合小波神经网络和遗传算法在香港衍生品市场上的研究［J］.系统管理学报，2008，17（1）：25-31.

ZHANG Hongyan，LIN Hui.Study on Hong Kong derivative market by applying hybrid wavelet neural network and genetic algorithm［J］.Journal of Systems & Management，2008，17（1）：25-31.

［21］张鸿彦，林辉.基于小波神经网络的期权定价模型［J］.东南大学学报（自然科学版），2007，37（4）：716-720.

uGM/ZzIt19+A9zFXrWTD7w==ZHANG Hongyan，LIN Hui.Option pricing models based on wavelet neural network［J］.Journal of Southeast University（Natural Science Edition），2007，37（4）：716-720.

［22］孙有发，邱梓杰，姚宇航，等.基于深度学习算法的行为期权定价［J］.系统管理学报，2021，30（4）：697-708.

SUN Youfa，QIU Zijie，YAO Yuhang，et al.Behavioral option pricing based on Deep-Learning algorithm［J］.Journal of Systems & Management，2021，30（4）：697-708.

［23］ROSS S A.Options and efficiency［J］.The Quarterly Journal of Economics，1976，90（1）：75-89.

［24］COX J C，ROSS S A.The valuation of options for alternative stochastic processes［J］.Journal of Financial Economics，1976，3（1/2）：145-166.

［25］ZHOU Haoyi，ZHANG Shanghang，PENG Jieqi，et al.Informer：Beyond efficient transformer for long sequence time-series forecasting［C］//Proceedings of the AAAI Conference on Artificial Intelligence.Menlo Park：AAAI，2021：11106-11115.

［26］KINGMA D P，BAJ.Adam：A method for stochastic optimization［DB/OL］.（2017-01-30）［2023-12-03］.https：//arxiv.org/abs/1412.6980.