基于改进的Canopy-k-means的大跨屋盖表面风荷载分区方法

摘 要：针对k-means聚类算法在大跨屋盖结构表面风荷载分区计算中，聚类数k值随机选取容易导致结果不稳定和计算效率低等问题，提出改进的Canopy-k-means聚类算法。首先，引入Canopy算法并对其初始阈值和聚类中心的选取方式进行改进，减少初始值选取的盲目性，以提高风荷载分区结果的可靠性；其次，通过改进Canopy算法对风荷载数据集进行预处理，快速准确地确定聚类数k值；第三，将改进Canopy算法与k-means结合使用，实现最优分类数k值的精准识别，使得改进的Canopy-k-means聚类算法进行大跨屋盖结构表面风荷载分区时能够快速准确地得到分区结果；最后，以一大跨柱面屋盖干煤棚结构为例，基于风洞试验所得结构表面风荷载数据测试结果，采用所提改进的Canopy-k-means聚类算法对其表面风荷载进行分区计算。结果表明，采用改进的Canopy-k-means聚类算法，将0°、50°和90°风向角时大跨屋盖表面风荷载划分为了3个不同的分区，其对应的SD值分别为2.36、3.51和2.52，较传统k-means聚类算法所得对应值明显降低，类内紧凑性和类间分散性明显提升。所提改进Canopy-k-means聚类算法能够快速准确地得到最优分区结果，对大跨屋盖表面风荷载分区具有工程参考价值。

关键词：薄壳结构；风荷载测压；风荷载分区；k-means聚类算法；Canopy算法

中图分类号：TU393.3；TU312.1

文献标识码：A

DOI：10.7535/hbkd.2024yx05008

Study on surface wind load zoning of long-span roof based on

improved Canopy-k-means algorithm

LI Yuxue 3，JI Jun1， DONG Yang1

（1.School of Civil Engineering， Shijiazhuang Tiedao University， Shijiazhuang， Hebei 050043， China;

2. Innovation Center for Wind Engineering and Wind Energy Technology of Hebei Province，

Shijiazhuang， Hebei 050043， China;

3. Key Laboratory of the Ministry of Education for Road and Railway Engineering Safety Assurance，

Shijiazhuang Tiedao University， Shijiazhuang， Hebei 050043， China）

Abstract：In order to solve the problem that random selection of clustering number k can easily lead to instability and low computational efficiency of k-means clustering algorithm in the zoning calculation of wind load on the surface of long-span roof structures， an improved Canopy-k-means clustering algorithm was proposed. Firstly， the Canopy algorithm was introduced， and the selection of its initial threshold and clustering center was improved to reduce the blindness of the initial value selection so as to improve the reliability of the results of wind load zoning. Secondly， the improved Canopy algorithm was used to preprocess the wind load dataset to determine the cluster number k quickly and accurately. Thirdly， the improved Canopy algorithm was combined with k-means to achieve the accurate identification of the optimal classification number k， so that the improved Canopy-k-means clustering algorithm can get the zoning results quickly and accurately when the wind load on the surface of long-span roof structure was divided. Finally， taking a long-span cylindrical roof dry coal shed structure as an example， based on the test results of the surface wind load data obtained from the wind tunnel test， the improved Canopy-k-means clustering algorithm was used to calculate the surface wind load. The results show that by using the improved Canopy-k-means clustering algorithm， the wind loads on the surface of long-span roofs at 0 °， 50 °and 90 °wind angles are divided into three different zones， and the corresponding SD values are 2.36，3.51 and 2.52，respectively， which are significantly lower than those obtained by the traditional k-means clustering algorithm， and the intra-class compactness and inter-class dispersion are obviously improved. Therefore， the improved Canopy-k-means clustering algorithm can obtain the optimal zoning results quickly and accurately， and has good engineering application value for wind load zoning on the surface of long-span roofs.

Keywords：thin shell structure; wind load measurement; wind load zone; k-means clustering algorithm; Canopy algorithm

近年来，随着大跨屋盖结构的广泛应用，由风荷载导致的结构破坏也时有发生，其中大跨结构抗风设计过程中风荷载的合理、高效处理是保证结构抗风安全的前提和基础[1-2]。目前，通常根据大跨屋盖结构表面风荷载取值的不同将其划分为不同区域，再根据各个区域的风荷载代表值进行结构抗风设计，而如何实现结构表面风荷载的合理、高效分区成为国内外学者关注的热点。

k-means聚类作为一种无监督学习方法，由于不需要事先标注训练数据，比较适合于结构表面风荷载分区这种无法事先确定类别的情况，因此被不少学者引入到风工程领域中进行结构表面风荷载分区研究。李丹煜等[3-4]基于k-means聚类算法建立了大跨屋盖表面风压系数快速分区方法，并借助大跨平屋盖和鞍形屋盖对方法的准确性进行了验证。聂燕松[5]在k-means聚类算法基础上建立了平均风荷载分区方法，并编制了风荷载分区程序。张建等[6]提出采用k-means聚类算法及SD有效性指标确定最优k值的大跨屋盖表面风荷载分区方法，并基于风洞试验数据将高低跨柱面屋盖的风压系数划分为5个区域。楼文娟等[7]根据风洞试验所得大跨度平屋面风压分布规律，将屋面分成9个区域，给出了各区域的风压系数，并指出施加分区表示的风荷载要优于单一体型系数表示的风荷载。潘钧俊等[8]基于风洞试验结果，总结了2类风场条件下底部开敞和封闭的鞍形索网屋盖体型系数的分布规律，据此将屋盖表面风荷载进行了分区，同时考察了底部开敞对鞍形屋盖风压分区结果的影响规律。孙瑛等[9]借助刚性模型风洞试验，给出了划分大跨度平屋盖表面脉动风压高斯和非高斯区域的标准，并通过区域划分揭示了不同区域脉动风压形成机理。YANG等[10]基于k-means聚类原理，提出了大跨屋盖表面风荷载的混合分区方法，并对鞍型屋盖表面极值风压进行了分区计算。ALRAWASHDEH等[11]基于风洞试验测试结果，针对美国及加拿大风荷载规范中关于平屋盖局部体型系数分区结果，给出了具体的修正建议。

本文基于k-means聚类算法在进行分区计算时，存在分类情况数过多、寻找最优分区结果工作量大、计算效率低的问题，提出改进的Canopy-k-means聚类算法，实现最优分类数k值的精准识别，并对不同风向角下的大跨屋盖结构表面风荷载进行合理分区。在此基础上，针对一大跨柱面屋盖干煤棚结构刚性模型，进行测压风洞试验，并对所得风荷载数据进行分区计算，以验证所提方法的有效性。

1 k-means聚类算法

1.1 算法原理

k-means聚类算法[12]是目前最常用的结构表面风荷载分区方法，可对给定的大跨屋盖结构表面测点风荷载数据样本集进行分区，具体如下。

1）将风洞试验测试所得大跨屋盖结构表面n个测点风荷载数据集表示为C={ci∣i= …，n}，并从中随机选取k个对象作为初始聚类数Mk={mj∣j= …，k}，用mj（j= …，k）表示初始聚类（簇）中心。将2个对象之间的欧氏距离表示为d（ci，mj）=|ci-mj|。

2）逐一计算每一测点到各个聚类中心的距离，把各个测点按照距离最近的原则，即|ci-mj|<|ci-ml|，j，l= …，k，l≠j，归入相应类别ci∈Mk。

3）根据步骤2）将风荷载数据集划分为k个类别，并分别取对应类别内所有测点的风荷载均值作为该类别的新聚类中心m*1，m*2，…，m*j；m*j=1nj∑ciMjci，j= …，k，其中nj为j分区中的风荷载个数。

4）按照新的聚类中心位置，重新计算各测点风荷载距离新类别聚类中心的距离，并重新进行归类。

5）重复步骤4），直到m*i=mi，i= …，k，该算法收敛时程序终止，得到最优的风荷载分区结果。

1.2 算法不足

由1.1可见，采用k-means聚类算法对结构表面风荷载分区计算中，需要事先随机给定聚类数k值，其通常需7df096ab855a3a132521902f9a28914065dd709fbe2a04df5a3b522d4486e2e1要根据经验主观设定，比如，有学者提出kmax≤n[13]或者kmax≤2ln n[14]（n为测点总数），上述处理方法在一定程度上解决了k值选取的随机性问题，但均是基于经验而不具备理论依据，可能导致聚类结果不稳定和计算效率低的问题。

2 改进的Canopy-k-means聚类算法

2.1 Canopy算法

如1.2所述，k-means聚类算法用于大跨屋盖结构表面风荷载分区时，存在k值选取理论依据不足的问题。据此，本文引入Canopy算法对风荷载数据集进行预处理，首先识别出可能的聚类中心，进而确定聚类数k，再利用k-means聚类算法得到风荷载最优分区结果。

Canopy算法是广泛用于数据聚类的方法[15-16]，比如，对物流仓库的订单分类分拣等，采用该算法可以降低聚类工作量，提高工作效率。该算法可实现数据粗聚类，分别采用近似距离度量的方法以及2个距离阈值比较的方法将数据集划分成多个可重叠的子集Canopy，通过快速近似比对处理。k-means聚类提供初始聚类数k值的精准预判。

但Canopy算法在聚类初值选取的过程中，初始阈值T1、T2和初始聚类中心是通过任意取值得到的，且该算法对初始阈值和初始聚类中心的选取较为敏感，会直接影响最终的聚类效果。基于此，本文提出通过对初始阈值T1、T2和初始聚类中心的选取方式进行改进[17]，减少初值选择的盲目性，进而提高风荷载分区结果的可靠性。

2.2 改进的Canopy算法

本文主要从初始阈值获取方式和初始聚类中心选取2个方面对Canopy算法进行改进。首先，计算所有风荷载数据的均值点，选取与均值点最近的测点作为初始聚类中心，然后计算均值点到所有测点的距离，最远距离记作L1，最近距离记作L2，并将（L1-L2）赋值给T1，将L1/2赋值给T2，使最终得到的聚类数目k更准确。具体步骤如下：

1）首先计算风荷载数据集C的均值点mean，然后求解该均值点与所有剩余测点之间的距离Di，Di=|mean-ci|；

2）将距离均值点的最远距离记作L1，最近距离记作L2，令初始阈值T1=L1-L2，T2=L1/2，取距离均值点最近的测点作为初始聚类中心；

3）计算该聚类中心与所有剩余测点之间的距离d=|ci-mj|，将距离d小于T1的数据点划分到一个Canopy中；

4）将距离d小于T2的测点从数据集中删除；

5）重复步骤2）—4），直到风荷载数据集为空，即每个测点数据均归到了相应的Canopy集；

6）最终得到多个Canopy集。

2.3 改进的Canopy-k-means聚类算法

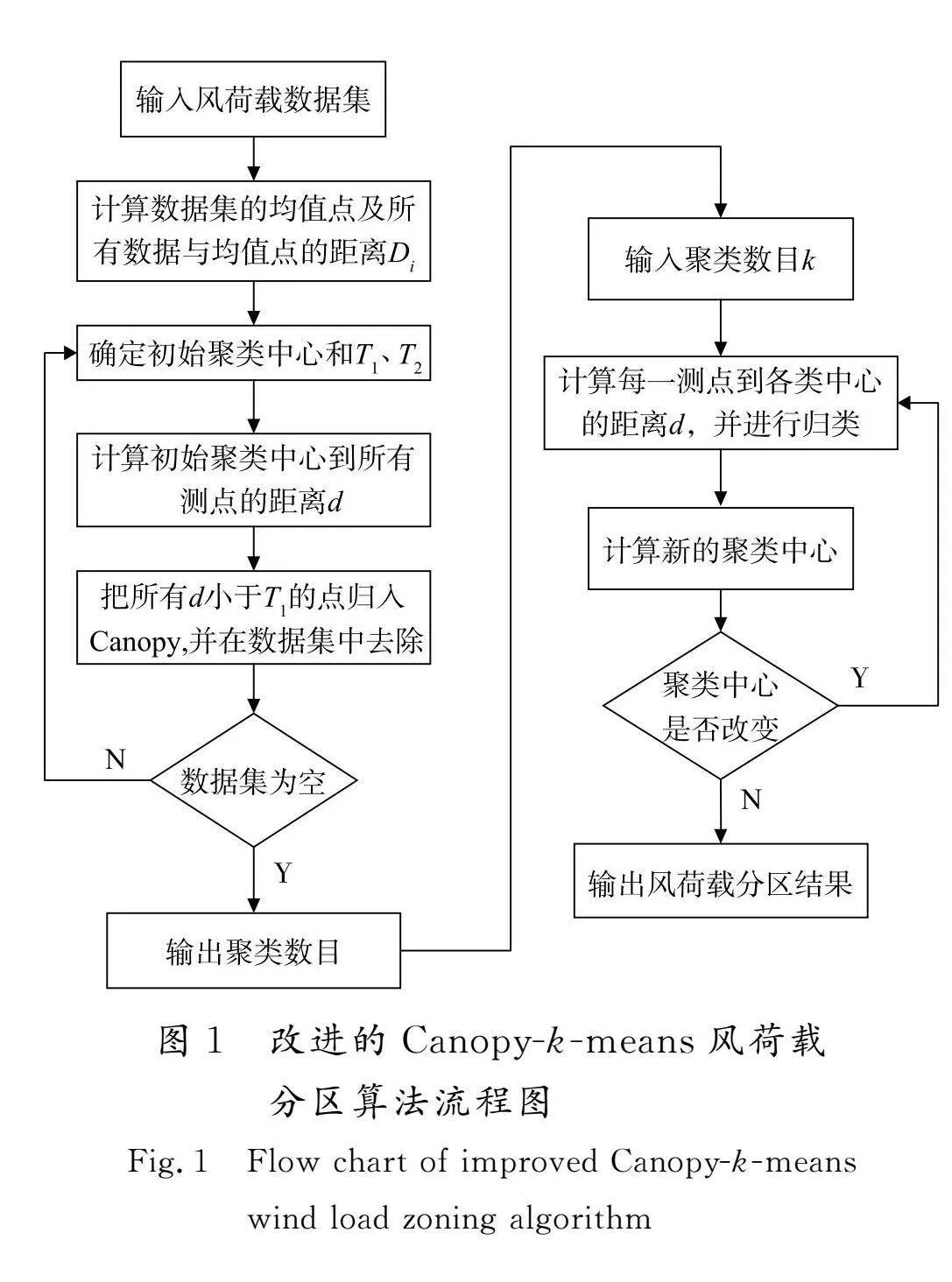
将k-means聚类算法、改进的Canopy算法结合使用[18]，实现最优分类数k值的精准识别，进而使得k-means聚类算法进行大跨屋盖结构表面风荷载分区时能够快速准确地得到分区结果。算法流程图如图1所示，具体步骤如下：

1）按照2.2改进的Canopy算法中步骤1）—6）对风荷载数据集进行预处理，得到初始聚类中心以及k个Canopy集，故k为风荷载数据集的初始聚类中心数目；

2）利用步骤1）所得初始聚类中心数目k，选取距离数据集均值点最近距离的k个对象作为初始聚类中心，逐一计算每一测点到各个聚类中心的距离d，再根据距离最近原则将每个测点归入相应的类别；

3）分别取对应类别内所有测点的风荷载均值作为该类别的新聚类中心，按照新聚类中心位置重新计算各测点风荷载与新聚类中心的距离d，再根据距离_{858de500e9296113cf00699070c715c32f5d8f4d3e6f0efbc699a0c3a9beb4ff}最近原则将每个测点重新分类；

4）直到分区结果和聚类中心不再变化，得到最终的风荷载分区结果。

2.4 SD值有效性检验

根据风荷载分区计算结果，引入SD有效性指标[19]，据此判定所提方法计算大跨屋盖结构风荷载分区的有效性，具体如下。

1）定义类内紧凑性判定指标S（k），S（k）值越大，表示类内紧凑性越低。

S（k）=1k∑km=1σ（pm）σ（p） ，（1）

式中：σ（p）为全部测点风荷载值的方差；σ（pm）为第m类内全部测点风荷载值的方差；k为分类数。

2）定义类间分散性判定指标D（k），D（k）值越大，表示类间分散性越小。

D（k）=DmaxDmin∑kt=1

∑ks=1（ct-cs）-1 ，（2）

式中：Dmax=max（|ct-cs|），Dmin=min（|ct-cs|），（t，s∈{ …，k}，t≠s），分别为第t、s 2类中心间最大和最小欧氏距离；ct为第t类内所有测点风荷载的均值；cs为第s类内所有测点风荷载的均值；k为分类数。

3）构造兼顾类内紧凑性和类间分散性的综合指标SD（k），此SD（k）值越小，表示类内越紧凑、类间越分散，综合分类结果越理想，由此可以检验所提方法对应大跨屋盖结构风荷载分区计算的有效性。

SD（k）=αS（k）+D（k） ，（3）

式中：α为加权因子，α=D（kmax）；kmax为分类数的最大值。

3 算例分析

为说明本文所提改进的Canopy-k-means聚类算法对大跨屋盖结构表面测点风荷载分区计算的有效性，以一大跨度封闭式柱面屋盖干煤棚结构为例，对风洞试验所得结构表面风荷载测试数据进行分区计算，并借助2.4中的SD有效性指标对方法的有效性进行验证。

3.1 工程简介

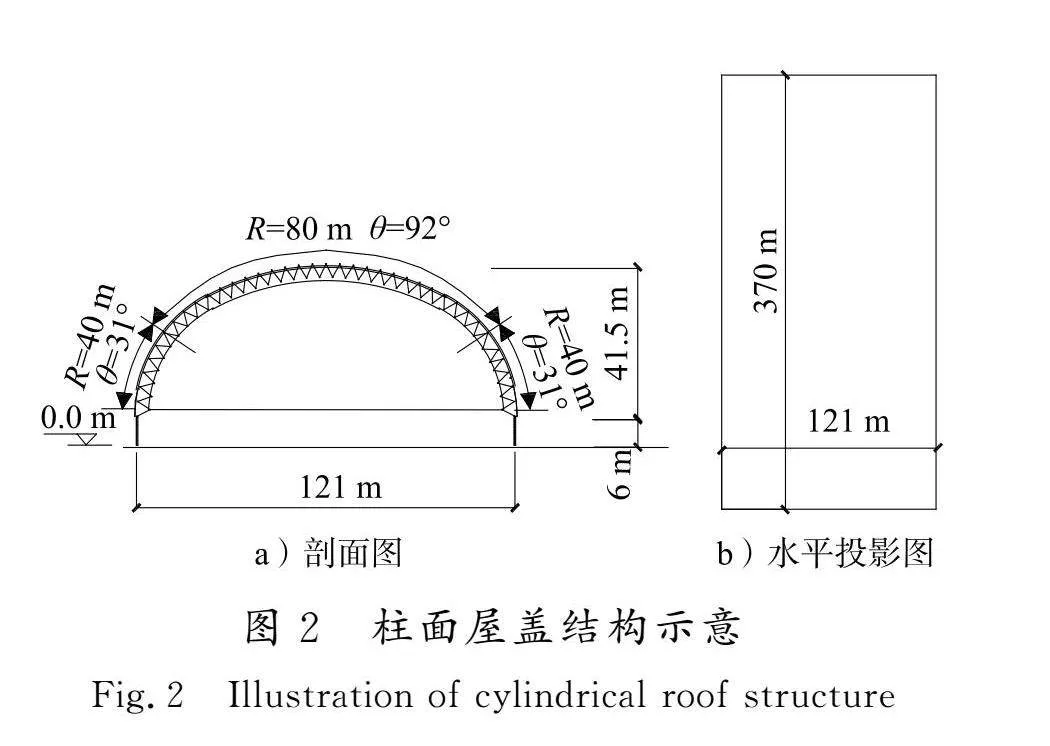
本文选取的大跨度封闭式柱面屋盖干煤棚结构如图2所示，其跨度121 m，长度370 m，结构总高度47.5 m，网壳曲面矢高41.5 m，矢跨比0.34，底面墙高6 m，两端封闭，柱壳面由中心一段半径R=80 m和两端半径R=40 m的圆弧组成，对应的圆心角θ分别为92°和31°。试验模型缩尺比 1∶200，采用有机玻璃与ABS板制成，保证其强度和刚度满足测压试验要求。

3.2 风洞试验测试

模型风荷载测压试验在石家庄铁道大学风工程研究中心大气边界层风洞的低速试验段完成，风洞试验模型缩尺比为1∶200，满足阻塞率小于3%的要求。在模型上、下表面各布置测压点357个（上、下表面对应布置），共布置714个，考虑到气流在该屋盖结构端部常常产生柱状涡或锥形涡，属于风荷载分布特性复杂且敏感区域，故在端部将测点加密（图3中的轴①和轴③所在区域），每个测压点采样点数为9 000，采样频率为312.5 Hz。在试验过程中，上、下表面同步测压，从0°～360°每隔10°风向角（风向角定义如图3所示）测试并采集数据1次。

3.3 风场模拟

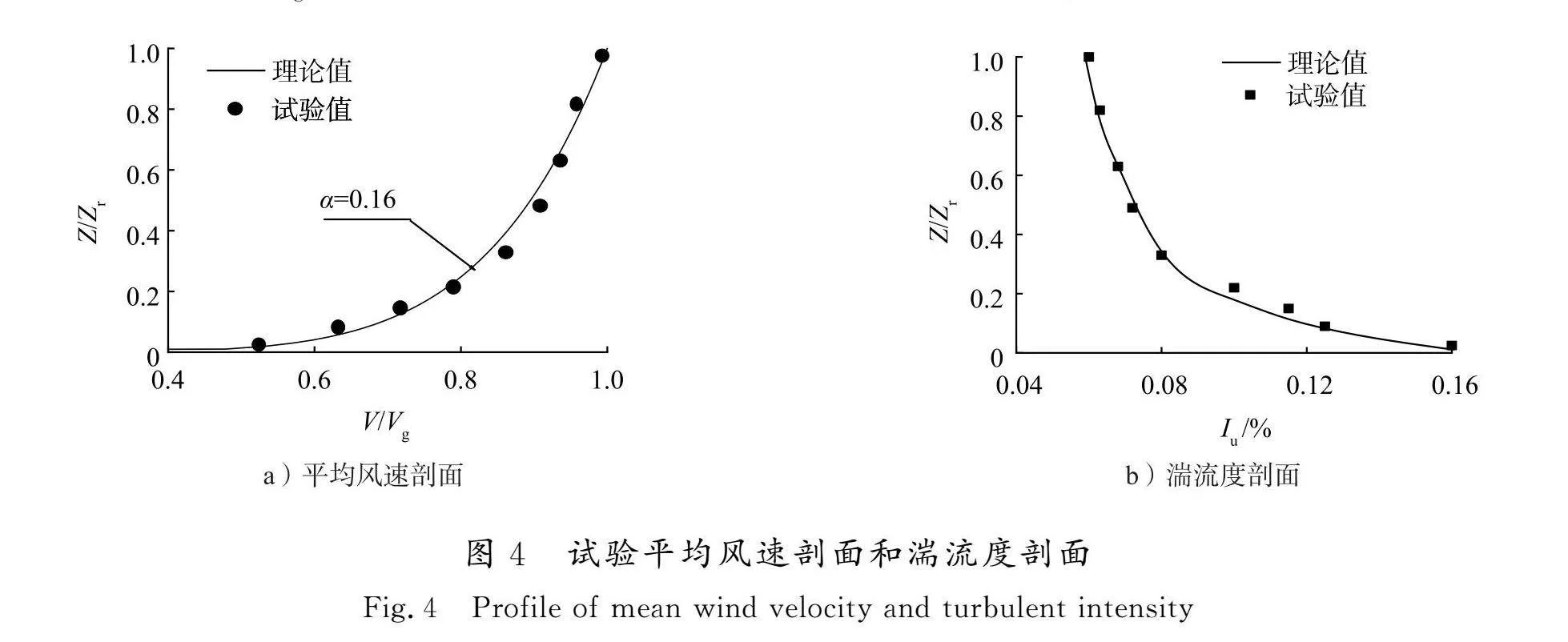
试验中采用尖劈格栅组合装置和地面粗糙元模拟GB 50009—2012《建筑结构荷载规范》[20]规定的B类地貌。图4为试验模拟的来流平均风速剖面和湍流度剖面，其中Z为高度，Zr为模型参考点高度（取屋盖最高处），V为平均风速，Vg为参考点风速（取10 m/s），对应的湍流强度Iu为0.06%。

3.4 测点风荷载数据处理方法

在研究中，对风压值符号定义如下：沿结构表面法线方向远离结构时为负压，表现为风吸力，反之为正压，表现为风压力。在对屋盖结构进行抗风分析时，通常关心的是其上、下表面受到的净风压，因此将模型上、下表面对应位置2个测点处的测压值进行叠加，作为该位置处的净风压值，即：

pi（t）=pui（t）-pdi（t） ，（4）

式中：pui（t）和pdi（t）分别为结构表面i测点位置上、下表面对应的测压值。

为了表达方便，将结构表面i测点位置的净风压值pi（t）处理为相应于参考点处风压的无量纲压力系数（风压系数），即：

Cpi（t）=pi（t）-p∞p0-p∞，（5）

式中：Cpi（t）为结构表面i测点位置处的风压系数；p0和p∞分别为测压试验中参考点处的净风压和静压。由式（5）可以得到结构表面i测点位置处的平均风压系数：

pi=∑Nm=1Cpi（tm）N ，（6）

式中：Cpi（tm）为tm时刻结构表面i测点位置处的压力系数；N为总的采样点数。

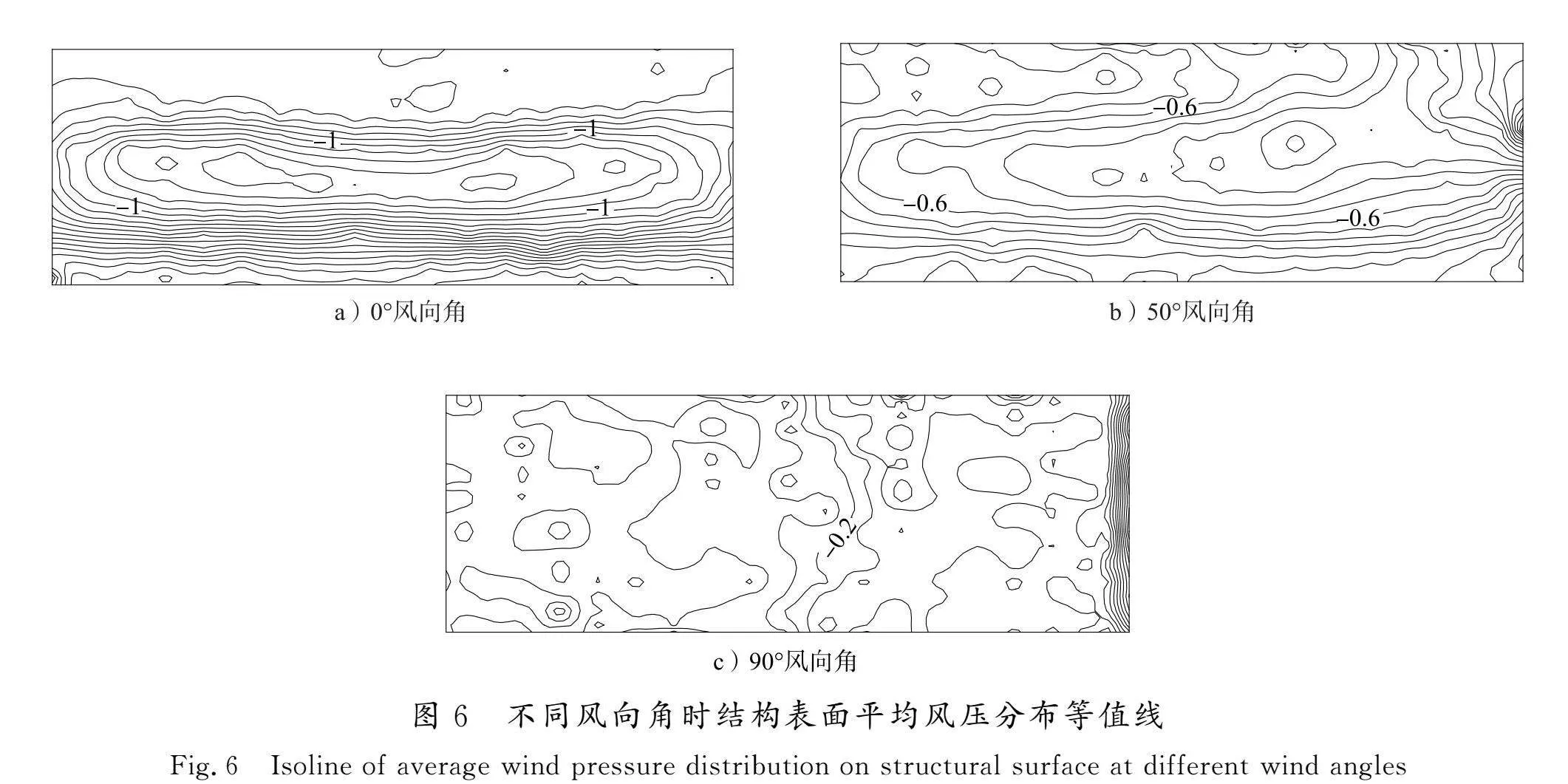
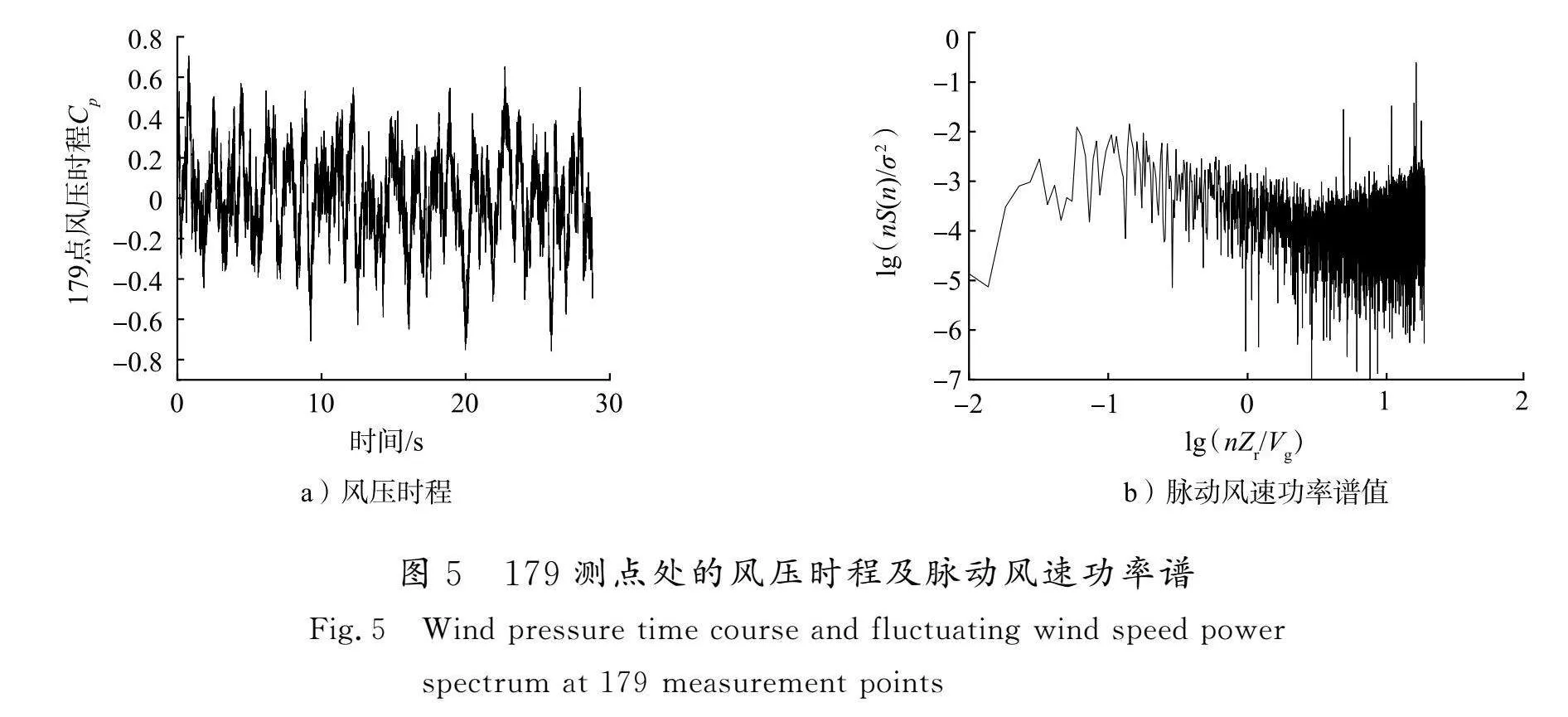
选取参考点处（179测点）测试结果，根据式（4）—（6）计算得到其0°风向角的风压时程，并转换为无量纲的功率谱如图5所示，同时，计算得到0°、50°、90° 3个代表性风向角时屋盖结构表面的平均风压系数分布等值线，如图6所示。

由图6可以看出，不同风向角时屋盖结构表面风荷载差别较大，且同一风向角下，风荷载数值具有一定的区域特征。因此，若能据此进行结构表面风荷载的合理分区，将有利于简化结构风效应分析时的风荷载施加。

4 基于改进的Canopy-k-means聚类算法的风荷载分区

4.1 改进的Canopy-k-means聚类算法分区

根据图5所得屋盖表面平均风压系数分布结果，采用所提改进的Canopy-k-means聚类算法，分别对0°、50°、90° 3个风向角时屋盖结构表面平均风压系数进行分区计算。因篇幅限制，本文以0°风向角时为例，具体过程如下：

1）计算得到0°风向角时屋盖表面平均风压系数据集的均值mean=-0.183，计算该均值点与所有剩余数据点之间的距离Di（i= …，357）。

2）从计算所得357个Di中，选取数值最大的记为L1=1.994，最小的记为L2=0.003，据此计算得到初始阈值T1=L1-L2=1.991，T2=L1/2=0.997，并取L2=0.003对应的162号测点平均风压系数值-0.047为初始聚类中心。

3）基于步骤2）所得的初始聚类中心和初始阈值T1和T2，由2.2改进的Canopy算法计算得到3个Canopy集，由此得到初始聚类中心数目k=3。

4）选取距离均值mean=-0.183最近的3个测点的平均风压系数值作为聚类中心，即测点162，232，339，对应的风压系数值分别为-0.047、-0.883、0.011。

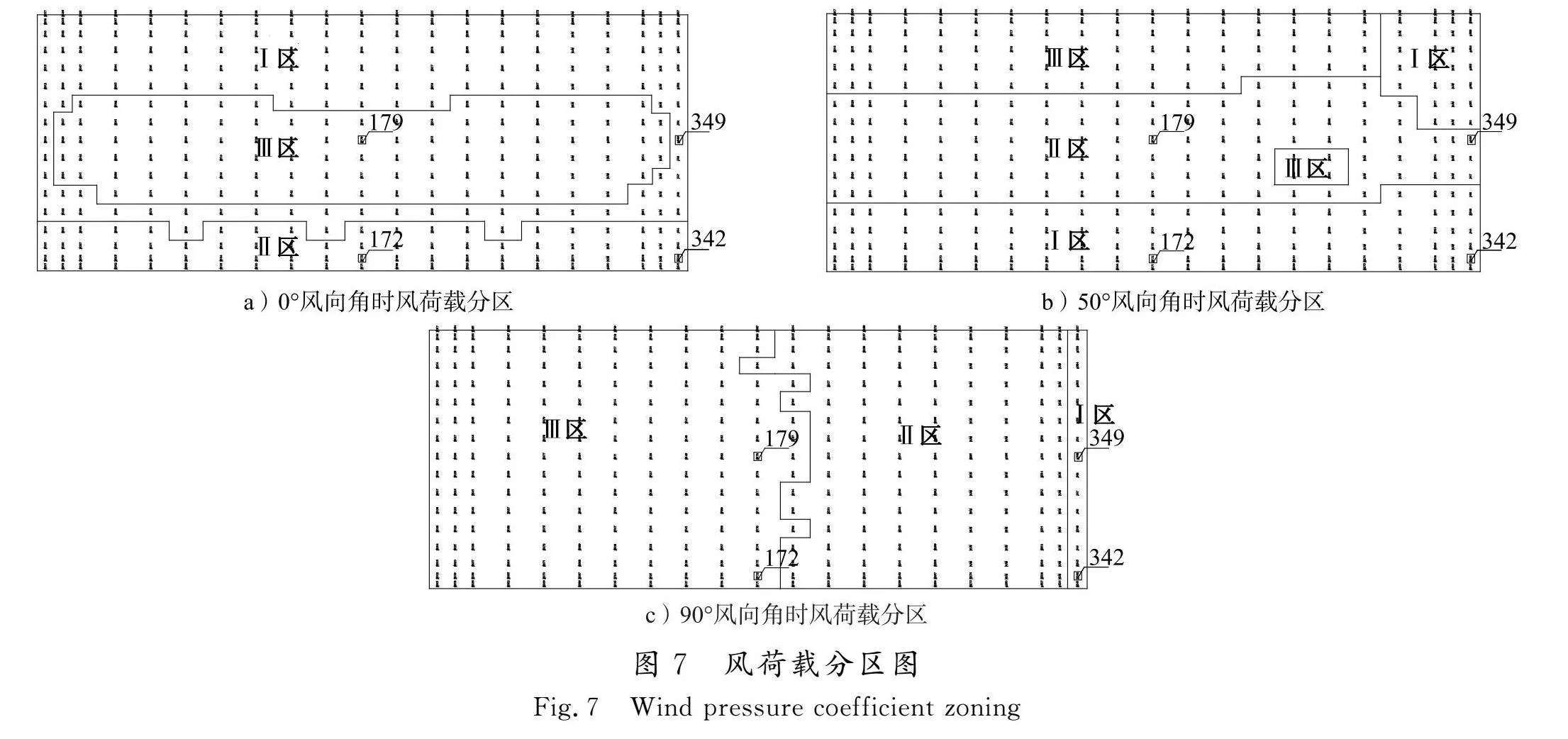
5）基于k-means聚类算法，经过352次迭代，分区结果和聚类中心不再发生变化，得到最终的0°风向角时平均风压系数测点3个分区结果（见表1），并将其示于图7。

同样，在表2计算参数下，根据图6 b）、c）所示50°、90°风向角时的风荷载数据，计算得到其测点分区结果（见表1）及分区图（见图7）。

由图7 a）可见，在0°风向角时，将屋盖表面风荷载分成3个区域，分别为迎风前缘撞击区、气流分离区以及再附着区，与图6 a）分布形式对应较好，其对应的风荷载代表值分别为0.525、1.185和0.198。同样，由图7 b）、c）可见，50°和90°风向角时，屋盖表面风荷载分区结果也较好反映了此风向角下屋盖表面特征湍流作用规律，且与图6 b）、c）分布形式基本对应。

4.2 SD值计算及与传统k-means算法对比

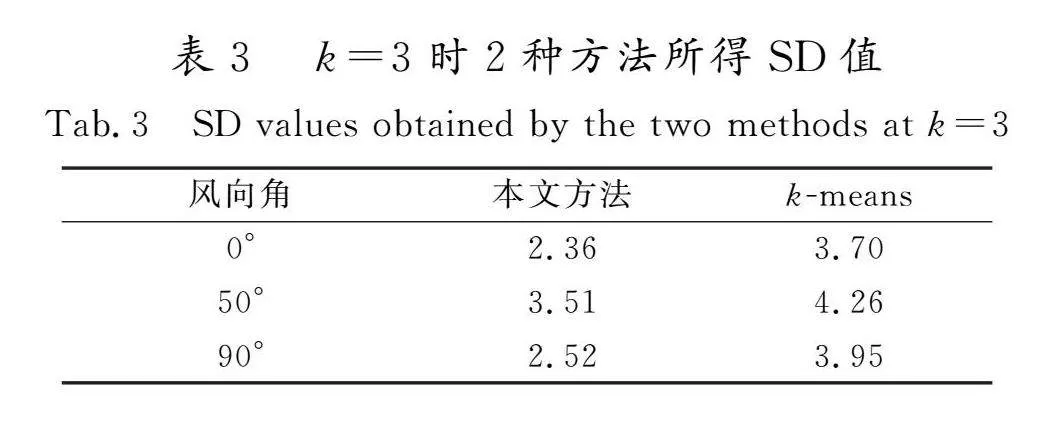
根据2.4思路，基于所提改进的Canopy-k-means聚类算法计算所得0°、50°和90°风向角时风荷载分区结果及对应的k值，计算得到相应的SD值如表3所示。另外，还基于传统的k-means算法对风洞试验所得0°、50°和90°风向角时进行了分区计算，其中初始分类数k值按照kmax≤n[13]或者kmax≤2ln n[14]选取，二者计算所得分别为k=357≈19和k=2ln（357）≈12，据此选取较小值kmax=12，在此范围内，为直观对比，0°、50°和90°风向角时分别取k=3，同样计算得到其相应的SD值，如表3所示。

由表3可见，采用k-means算法和改进的Canopy-k-means对算例中悬挑屋盖表面平均风压系数进行分区计算，改进的算法所得的分区数目k=3对应的SD值均小于k-means算法k=3时计算所得的SD值，表明改进的Canopy-k-means聚类算法优于传统k-means算法，且可以直接识别得到最优分类数k值，能快速准确地得到最优分区结果，计算效率显著提高。

5 结 语

对Canopy算法进行了改进，优化了初始阈值T1、T2和初始聚类中心选取方式，减少了初始值选择的盲目性，进而提高了风荷载分区结果的可靠性，并且能够快速有效地得到大跨屋盖结构表面风荷载数据的最佳聚类数目k。改进的Canopy-k-means聚类算法能快速准确地对大跨屋盖结构在不同风向下的风荷载进行合理分区，提高了计算效率并为该类屋盖结构抗风设计提供参考依据。

本文方法对数据预处理要求较高，噪声数据可能会对聚类结果产生不良影响。未来拟针对不同体型的大跨屋盖结构，分别以表格形式给出其表面风荷载的分区结果，以有效避免数据预处理的复杂度并更加方便工程应用。

参考文献/References：

[1] ZOU

Qiong，LI Zhengnong，ZENG Xuan，et al.The analysis of characteristics of wind field on roof based on field measurement[J].Energy and Buildings，2021.DOI： 10.1016/j.enbuild.2021.110877.

[2] 王瑞琦.基于CFD数值模拟的环形大跨度屋盖结构抗风可靠性分析[D].桂林：桂林理工大学，2019.

WANG Ruiqi.Wind-Resistant Reliability Analysis of Long-Span Roof Structure Based on CFD Numerical Simulation[D].Guilin：Guilin University of Technology，2019.

[3] 李丹煜，杨庆山，田玉基.大尺度平屋盖聚类最优风压分区研究[J].建筑结构学报，2013，34（9）：91-96.

LI Danyu，YANG Qingshan，TIAN Yuji.Study on clustering optimal design zones of wind pressure on large-scale flat roof[J].Journal of Building Structures，2013，34（9）：91-96.

[4] 李丹煜，杨庆山，田玉基.基于K-means聚类的风压系数快速分区方法[J].工程力学，2014，31（12）：164-172.

LI Danyu，YANG Qingshan，TIAN Yuji.A quick zoning method for wind pressure coefficients based on K-means clustering[J].Engineering Mechanics，2014，31（12）：164-172.

[5] 聂燕松.大跨屋盖结构分区设计风荷载研究[D].哈尔滨：哈尔滨工业大学，2018.

NIE Yansong.Research on Partition Design Wind Load of Large-Span Roof[D].Harbin：Harbin Institute of Technology，2018.

[6] 张建，杨娜，杨光，等.大尺度高低跨柱面屋盖的风压系数分区研究[J].建筑结构学报，2018，39（sup）：23-28.

ZHANG Jian，YANG Na，YANG Guang，et al.A zoning method of wind pressure coefficients on a large-scale unequal-height cylindrical roof[J].Journal of Building Structures，2018，39（sup）：23-28.

[7] 楼文娟，李本悦，陆峰.大跨度屋面风压分布拟合公式及风荷载取值[J].同济大学学报（自然科学版），2002，30（5）：588-593.

LOU Wenjuan，LI Benyue，LU Feng.Fitting formula to wind pressure distribution on long-span roofs and wind load suggestion[J].Journal of Tongji University（Natural Science），2002，30（5）：588-593.

[8] 潘钧俊，李方慧，顾明，等.不同风场开敞和封闭的鞍形屋盖平均风压特性[J].同济大学学报（自然科学版），2009，37（6）：715-719.

PAN Junjun，LI Fanghui，GU Ming，et al.Mean wind pressure characteristics on saddle roof with or without enclosed wall under different terrain conditions[J].Journal of Tongji University（Natural Science），2009，37（6）：715-719.

[9] 孙瑛，苏宁，武岳.典型大跨度屋盖结构的风压谱工程简化模型[J].建筑结构学报，2019，40（7）：23-33.

SUN Ying，SU Ning，WU Yue.Engineering model of wind pressure spectra on typical large-span roof structures[J].Journal of Building Structures，2019，40（7）：23-33.

[10]YANG Qingshan，YIN Jiaqi，LIU Min，et al.A zoning method for the extreme wind pressure coefficients of buildings based on weighted K-means clustering[J].Journal of Wind Engineering and Industrial Aerodynamics，2022.DOI： 10.1016/j.jweia.2022.105124.

[11]ALRAWASHDEH H，STATHOPOULOS T.Wind pressures on large roofs of low buildings and wind codes and standards[J].Journal of Wind Engineering and Industrial Aerodynamics，2015，147：212-225.

[12]曲福恒，潘曰涛，杨勇，等.基于加权空间划分的高效全局K-means聚类算法[J/OL].吉林大学学报（工学版）.（2022-12-16）[2023-12-10].https：//doi.org/10.13229/j.cnki.jdxbgxb20221338.

QU Fuheng，PAN Yuetao，YANG Yong， et al. An efficient global K-means clustering algorithm based on weighted space partitioning[J/OL].Journal of Jilin University（Engineering and Technology Edition）.（2022-12-16）[2023-12-10].https：//doi.org/10.13229/j.cnki.jdxbgxb20221338.

[13]SHAHAPURE K R，NICHOLAS C.Cluster quality analysis using silhouette score[C]//2020 IEEE 7th International Conference on Data Science and Advanced Analytics （DSAA）.Sydney：IEEE，2020：747-748.

[14]范九伦，裴继红，谢维信.模糊相关度与聚类有效性[J].西安电子科技大学学报，1998，25（1）：18-21.

FAN Jiulun，PEI Jihong，XIE Weixin.Fuzzy relation degree and cluster validity[J].Journal of Xidian University，1998，25（1）：18-21.

[15]孟佳伟，孙红.基于Hadoop平台的K-means算法优化综述[J].软件导刊，2017，16（6）：208-211.

MENG Jiawei，SUN Hong.Summary of K-means algorithm optimization based on Hadoop platform[J].Software Guide，2017，16（6）：208-211.

[16]胡小建，韦超豪.基于Canopy和k-means算法的订单分批优化[J].合肥工业大学学报（自然科学版），2017，40（3）：414-419.

HU Xiaojian，WEI Chaohao.Order batching optimization based on Canopy and k-means algorithm[J].Journal of Hefei University of Technology（Natural Science），2017，40（3）：414-419.

[17]鲁茜，蒙祖强.Canopy算法中T值选取的优化及聚类效果的改进[J].信息与电脑，2021，33（6）：61-65.

LU Qian，MENG Zuqiang.Optimization of T value selection and improvement of clustering effect in Canopy algorithm[J].Information & Computer，2021，33（6）：61-65.

[18]王海燕，崔文超，许佩迪，等.Canopy在划分聚类算法中对K选取的优化[J].吉林大学学报（理学版），2020，58（3）：634-638.

WANG Haiyan，CUI Wenchao，XU Peidi，et al.Optimization of Canopy on K selection in partition clustering algorithm[J].Journal of Jilin University（Science Edition），2020，58（3）：634-638.

[19]LIANG Shaoyi，HAN Deqiang，YANG Yi.Cluster validity index for irregular clustering results[J].Applied Soft Computing，2020.DOI： 10.1016/j.asoc.2020.106583.

[20]GB 50009—2012，建筑结构荷载规范[S].